Колебания и волны. Гармонические колебания презентация

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Виды и признаки колебаний
В физике особенно выделяют колебания двух видов – механические и электромагнитные и их электро-механические комбинации, поскольку они чрезвычайно актуальны для жизнедеятельности человека.
Колебательным движением называются процес-сы, отличающиеся той или иной степенью повто-ряемости во времени.
Для колебаний характерно превращение одного вида энергии в другой – кинетической в потенциальную, магнитной в электрическую и т.д.
Простейшим примером периодического движения служат колебания груза на конце пружины.
Будем считать, что массой пружины можно пренебречь и что пружина установлена горизонтально.

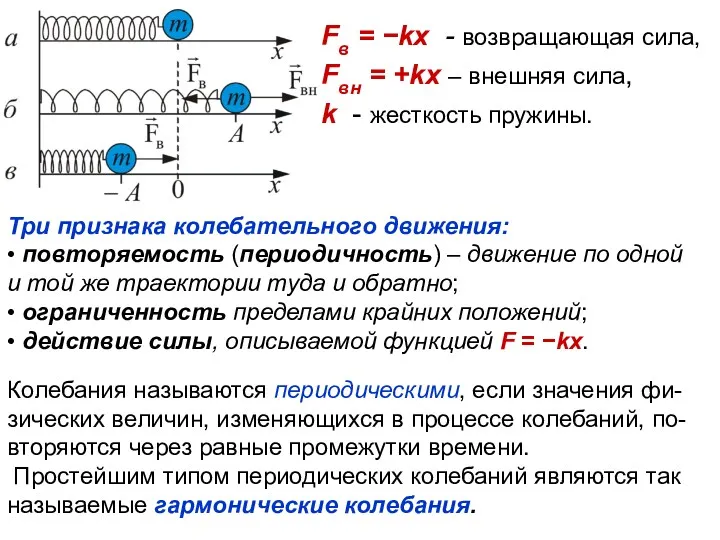
о
Fв = −kx - возвращающая сила,
Fвн = +kx – внешняя сила,
k - жесткость пружины.
Три признака колебательного движения:
• повторяемость (периодичность) – движение по одной и той же траектории туда и обратно;
• ограниченность пределами крайних положений;
• действие силы, описываемой функцией F = −kx.
Колебания называются периодическими, если значения фи-зических величин, изменяющихся в процессе колебаний, по-вторяются через равные промежутки времени.
Простейшим типом периодических колебаний являются так называемые гармонические колебания.

Любая колебательная система, в которой возвращаю-щая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, F = −kx ), со-вершает гармонические колебания.
Саму такую систему часто называют гармоническим осциллятором.
1) Колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
2)Различные периодические процессы можно пред-ставить как наложение гармонических колебаний.
Периодический процесс можно описать уравнением:
f(t) = f (t + nT) .
По определению, колебания называются гармоничес-кими, если зависимость некоторой величины x = f (t) имеет вид
x = Asin φ или x = Acosφ (6.1)
Здесь синус или косинус используются в зависимости от условия задачи, А и φ – параметры колебаний.

2. Параметры гармонических колебаний
Расстояние груза от положения равновесия до точки, в которой находится груз, называют смещением x.
Максимальное смещение – наибольшее расстояние от положения равновесия – называется амплитудой и обо-значается буквой A.
Выражение, стоящее под знаком синуса или косинуса в формуле (6.1) φ = ωt + φ0 , определяет смещение x в дан-ный момент времени t и называется фазой колебания.
При t =0 φ = φ0, поэтому φ0 называется начальной фазой колебания. Фаза измеряется в радианах и определяет зна-чение колеблющейся величины в данный момент времени.
Движение от некоторой начальной точки до возвращения в ту же точку, например от x = A к x = −A и обратно в x = A, называется полным колебанием.
Частота колебаний ν определяется как число полных колебаний в 1 секунду. Частоту, как правило, измеряют в герцах (Гц): 1 Гц равен 1 полному колебанию в секунду.

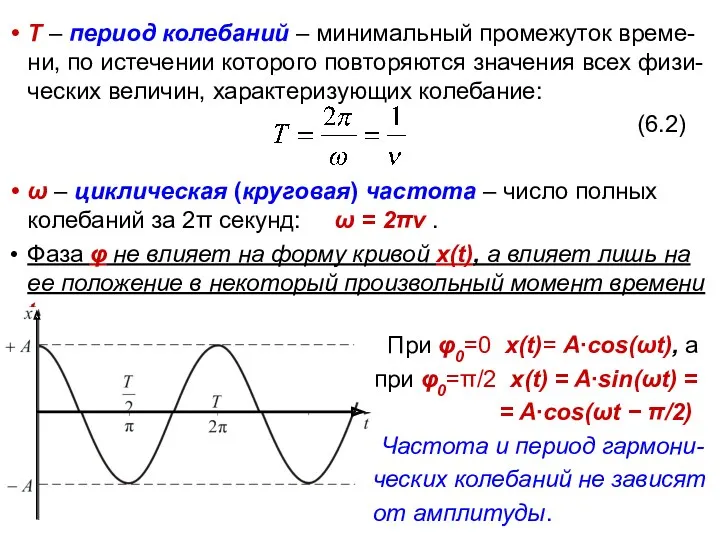
Т – период колебаний – минимальный промежуток време-ни, по истечении которого повторяются значения всех физи-ческих величин, характеризующих колебание:
(6.2)
ω – циклическая (круговая) частота – число полных колебаний за 2π секунд: ω = 2πν .
Фаза φ не влияет на форму кривой х(t), а влияет лишь на ее положение в некоторый произвольный момент времени t.
При φ0=0 x(t)= A∙cos(ωt), а
при φ0=π/2 x(t) = A∙sin(ωt) =
= A∙cos(ωt − π/2)
Частота и период гармони-
ческих колебаний не зависят
от амплитуды.

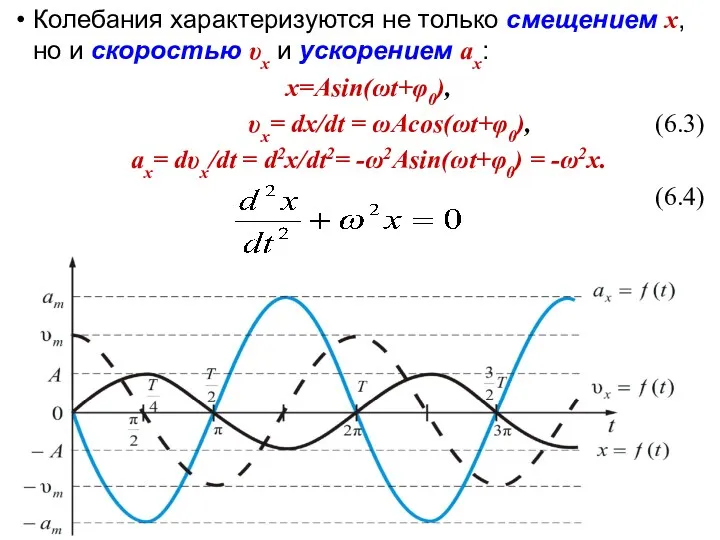
Колебания характеризуются не только смещением х, но и скоростью υx и ускорением ax:
x=Asin(ωt+φ0),
υx= dx/dt = ωAcos(ωt+φ0), (6.3)
ax= dυx/dt = d2x/dt2= -ω2Asin(ωt+φ0) = -ω2x.
(6.4)

3. Механические гармонические колебания (на примере маятников)
Если физическую систему, обладающую состоянием устойчивого равновесия, вывести из этого состояния каким-либо внешним воз-действием и затем предоставить самой себе, то возникающие в системе колебания вблизи устойчивого равновесия называют собственными или свободными.
Способную совершать собственные колебания систему называют осциллятором. Примером линейных (одномерный случай) ос-цилляторов могут служить маятники (рис.): а) пружинный (груз на пружине); б) крутильный (диск на проволоке); в) математи-ческий (материальная точка на нерастяжимой нити); г) физический (С – центр масс твердого тела, О – точка прохождения оси коле-баний, перпендикулярной плоскости чертежа).

Рассмотрим случай а)– пружинный маятник.
Второй закон Ньютона для колеблющегося тела для одномерного случая можно записать в виде: m∙ax = Fx = -k∙x или
x = Xmax∙cos(ω0t +φ0)
Система, совершающая колебания под действием квазиупругой си-лы , называется линейным гармоническим осциллятором (ЛГО).
Кинетическая энергия материальной точки (колеблющегося тела):

Потенциальная энергия ( пружинный маятник):
Полная механическая энергия:
Классическая колеблющаяся точка не может выйти за границы отрезка [−xmax;+xmax], т.е. находится в потенциальной яме параболической фор-мы.
Колебания Wk и Wn совершаются со сдвигом по фазе на π и, следо-вательно, полная механическая энергия материальной точки при свободных незатухающих гармонических колебаниях не изменяется со временем (const).

г) физический маятник
Физический маятник – твердое тело, которое может совершать колебания под действием собственной силы тяжести mg вокруг неподвижной горизонтальной оси, не проходящей через центр масс тела и называемой осью качания. Центр тяжести маятника совпадает с его центром масс. Как правило, силой трения в под-весе маятника пренебрегают и момент относительно оси качания маятника создает только его сила тяжести mg.
При отклонении маятника на угол α момент,
создаваемый силой тяжести равен:
M = mgd sinα .
Согласно основному уравнению динамики
вращательного движения (для тела с момен-
том инерции I, вращающегося вокруг непод-
вижной оси в отсутствие трения):
При малых α → sinα ≈ α →

Сравнивая с уравнением свободных незатухающих гармонических колебаний: d2x/dt2 + ω2x = 0 , имеем для физического маятника:
Предельным случаем физического маятника является математичес-кий маятник - материальная точка, подвешенная на невесомой не-растяжимой нити и совершающая колебания в вертикальной пло-скости под действием силы тяжести. Вся масса сосредоточена в центре масс тела. При этом d=l – длина маятника и момент инер-ции J = ml2. Тогда
Длина математического маятника, имеющего такой же период ко-лебаний, что и данный физический маятник, называется приве-денной длиной физического маятника. Точка О1, находящаяся на расстоянии lпр от точки подвеса О маятника, называется центром качания физического маятника. Точки O и О1 обладают свойством взаимности, т.е. при перемене их ролей длина и период маятника останутся прежними.

Свободные гармонические колебания в электрическом
колебательном контуре
Простейшим колебательным контуром является замкнутая цепь,
состоящая из емкости C и катушки индуктивности L.
По закону Ома для замкнутой цепи: сумма падений
напряжений на проводниках сопротивлением R и на
конденсаторе Uс равна ЭДС самоиндукции в контуре
IR + Uc = IR + Q/C = εsi = -L(dI/dt).
I = dQ/dt → dI/dt = d2Q/dt2,
(R→0) → d2Q/dt2 + ω2Q =0
Q =Qmsin(ωt + φ0) и I = dQ/dt = ωQmcos(ωt + φ0) = Imcos(ωt + φ0)
W = Wэл + Wмагн = (1/2)∙(LI2 + CU2)

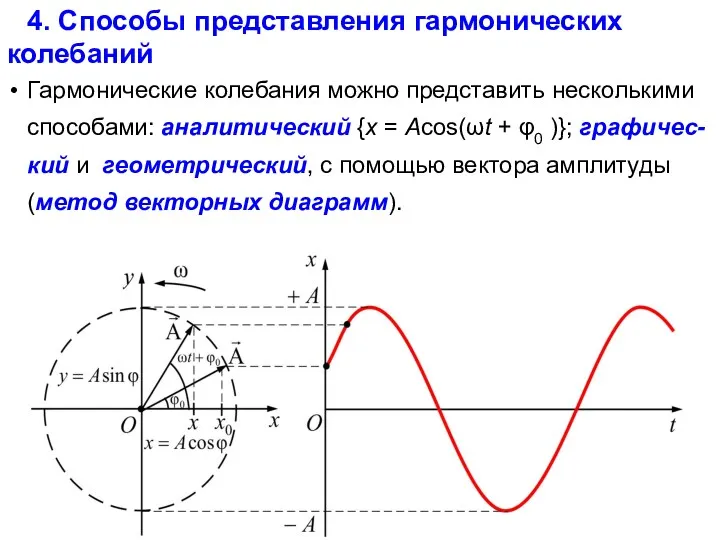
4. Способы представления гармонических колебаний
Гармонические колебания можно представить несколькими способами: аналитический {x = Acos(ωt + φ0 )}; графичес-кий и геометрический, с помощью вектора амплитуды (метод векторных диаграмм).

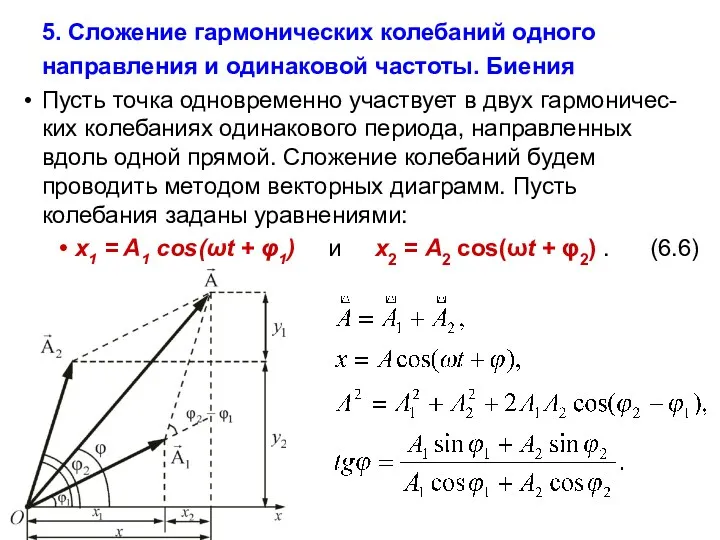
5. Сложение гармонических колебаний одного
направления и одинаковой частоты. Биения
Пусть точка одновременно участвует в двух гармоничес-ких колебаниях одинакового периода, направленных вдоль одной прямой. Сложение колебаний будем проводить методом векторных диаграмм. Пусть колебания заданы уравнениями:
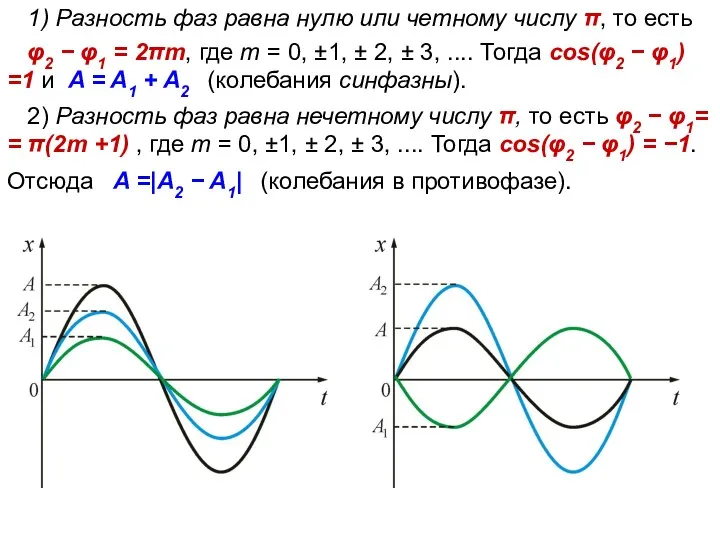
x1 = A1 cos(ωt + φ1) и x2 = A2 cos(ωt + φ2) . (6.6)

1) Разность фаз равна нулю или четному числу π, то есть
φ2 − φ1 = 2πm, где m = 0, ±1, ± 2, ± 3, .... Тогда cos(φ2 − φ1) =1 и A = A1 + A2 (колебания синфазны).
2) Разность фаз равна нечетному числу π, то есть φ2 − φ1= = π(2m +1) , где m = 0, ±1, ± 2, ± 3, .... Тогда cos(φ2 − φ1) = −1. Отсюда A =|A2 − A1| (колебания в противофазе).

Когерентными называются колебания, разность фаз которых во времени постоянна; т.к. ∆Ф(t) = (ω2 − ω1)t + (ϕ2 − ϕ1 ) = const , то это выполняется при ω2= ω1= ω, тогда x = x1+ x2= Asin(ωt+ϕ), где
А амплитуда и Ф=(ωt+ϕ) фаза результирующего колебания. Тогда в зависимости от значения (ϕ2 −ϕ1) результирующая амплитуда А изменяется в пределах от A = |A1 − A2| при ϕ2 -ϕ1 = ±(2m +1)π, до A = |A1 + A2| при ϕ2 -ϕ1 = ±2 π m (m → целые числа).
При ϕ2 -ϕ1 = ±2 π m колебания называются синфазными (в одной фазе), а при ϕ2 -ϕ1 = ±(2m +1)π – противофазными.
При ω1 ≠ ω2 результирующий вектор A будет изменяться по длине и вращаться с переменной скоростью. При сложении колебаний с близкими частотами (Δω=|ω2 −ω1|<<ω) возникают, так называе-мые, биения, тогда x1 = Acosωt, x2 = Acos(ωt + Δωt).

[2ωt >>Δω; cos(-Δωt)=cos(Δωt)]
Косинус берется по модулю, так как функция четная и поэтому частота биений ωб = Δω, а не Δω/2. Период биений равен поло-вине периода модуляции:
Тб = Тмод /2 = 2π/(Δω)

Вообще, колебания вида x = A(t)cos[ωt + φ(t)] называются модулированными. Частные случаи: амплитудная моду-ляция и модулирование по фазе или частоте. Биение – простейший вид модулированных колебаний.
Любые сложные периодические колебания S=f (t) можно представить в виде суперпозиции одновременно совершаю-щихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными цикличес-кой частоте ω:
Представление периодической функции в таком виде связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье (то есть представление сложных модулированных колебаний в виде ряда (суммы) простых гармонических колебаний). Слагаемые ряда Фурье, определяющие гармонические колебания с ча-стотами ω, 2ω, 3ω, ..., называются первой (или основной), второй, третьей и т.д. гармониками сложного периодического колебания.

6. Сложение взаимно перпендикулярных колебаний
Пусть некоторое тело колеблется и вдоль оси x, и вдоль оси y, т.е. участвует в двух взаимноперпендикулярных колебани-ях: x = A1 cos(ω1t + φ1) ; y = A2 cos(ω2t + φ2 ) .
Найдем уравнение результирующего колебания. Для прос-тоты примем ω1 = ω2 = ω. Разность фаз между обоими коле-баниями равна: Δφ = φ2 − φ1 . Чтобы получить уравнение траектории, надо исключить из этих уравнений время t.
Упростим выражения, выбрав начало отсчета так, чтобы
φ1 = 0 , т.е. x = A1 cosωt ; y = A2 cos(ωt + Δφ) .
или

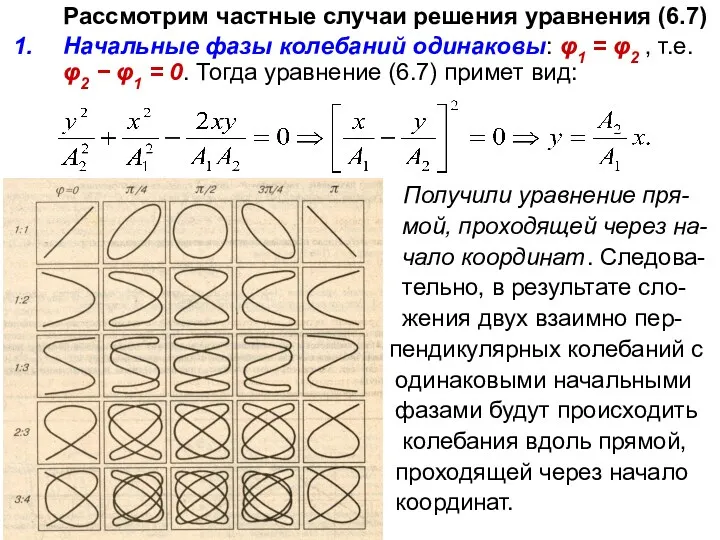
Возведем обе части в квадрат, сгруппируем и получим окончательное уравнение:
(6.7)
В результате мы получили уравнение эллипса, оси которого ориентированы относительно x и y произвольно.

Рассмотрим частные случаи решения уравнения (6.7)
Начальные фазы колебаний одинаковы: φ1 = φ2 , т.е. φ2 − φ1 = 0. Тогда уравнение (6.7) примет вид:
Получили уравнение пря-
мой, проходящей через на-
чало координат. Следова-
тельно, в результате сло-
жения двух взаимно пер-
пендикулярных колебаний с
одинаковыми начальными
фазами будут происходить
колебания вдоль прямой,
проходящей через начало
координат.

7. Свободные затухающие механические колебания
Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно умень-шается (затухает). Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызываю-щие затухание колебаний, пропорциональны величине ско-рости (например маятник). Тогда сила трения (или сопротив-ления): Fтр = -r∙v,
где r – коэффициент сопротивления, v – скорость движения.

Однородное дифференциальное уравнение второго по-рядка, описывающее затухающее колебательное дви-жение, запишется в виде:
Решение этого уравнения имеет вид:
Здесь А0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения.
где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний.

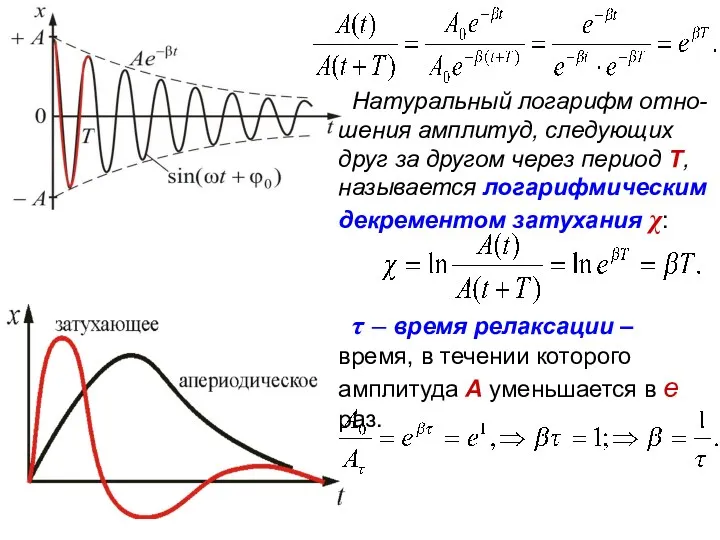
Натуральный логарифм отно-шения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
τ – время релаксации – время, в течении которого амплитуда А уменьшается в е раз.

Следовательно, коэффициент затухания β есть физи-ческая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда умень-шается в e раз. Тогда:
τ = NТ; → T = τ/N; →β = 1/τ
Следовательно, логарифмический декремент затуха-ния χ есть физическая величина, обратная числу колеба-ний, по истечении которых амплитуда А уменьшается в e раз.