Содержание
- 2. Выпуклые многогранники
- 3. 1752 год
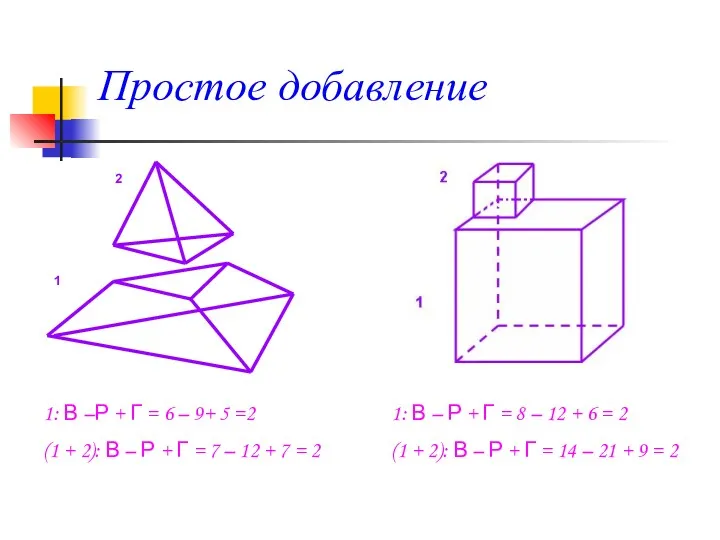
- 4. Простое добавление 1: В –Р + Г = 6 – 9+ 5 =2 (1 + 2):
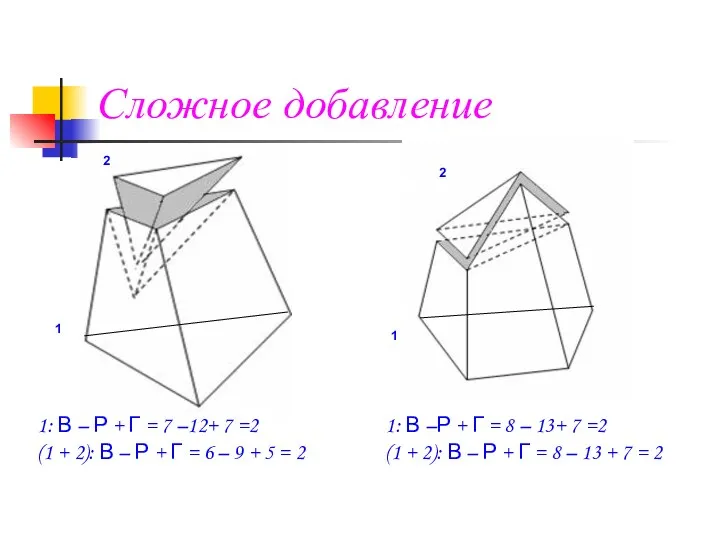
- 5. Сложное добавление 1: В –Р + Г = 8 – 13+ 7 =2 (1 + 2):
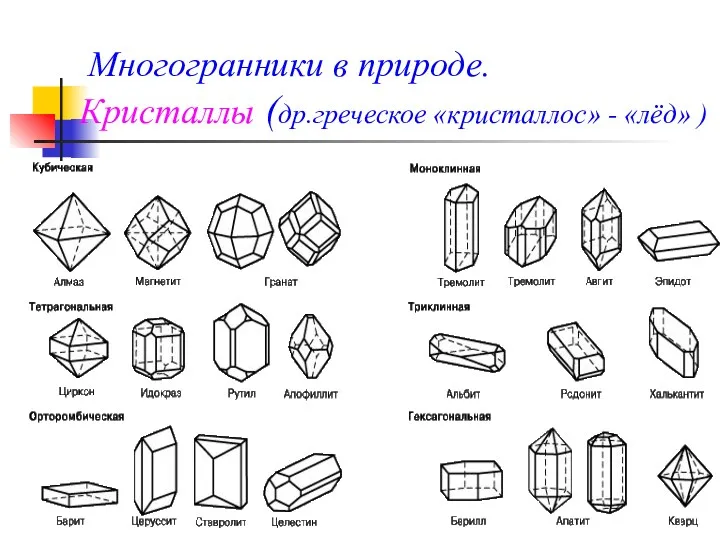
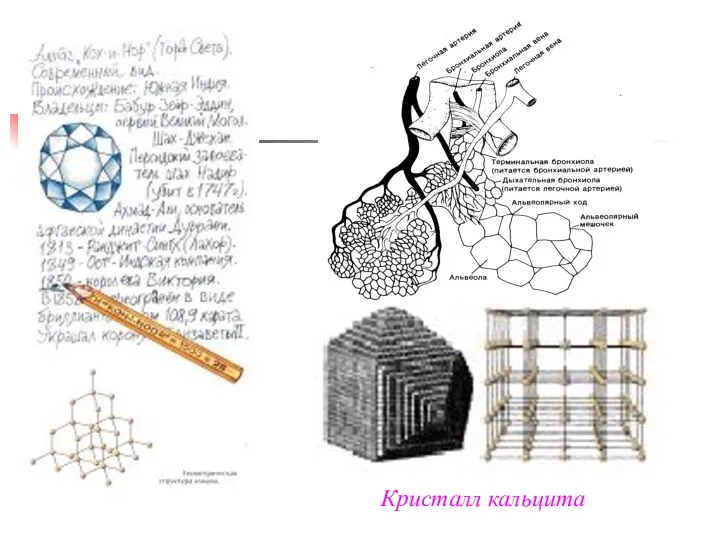
- 6. Многогранники в природе. Кристаллы (др.греческое «кристаллос» - «лёд» )
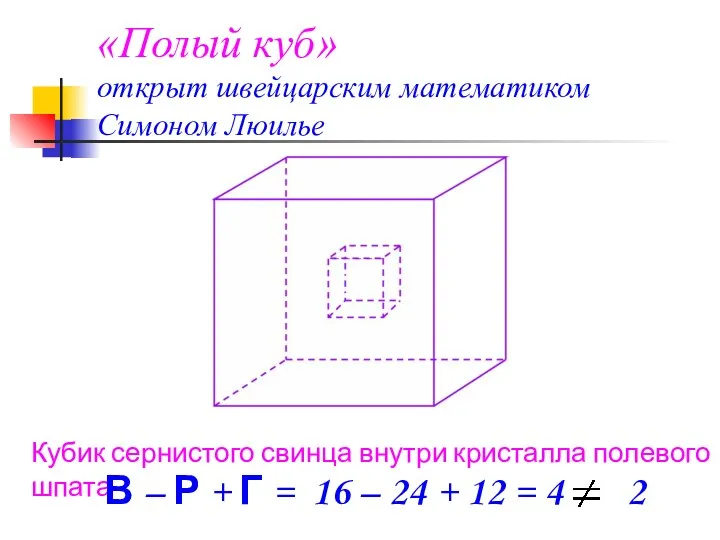
- 7. Кубик сернистого свинца внутри кристалла полевого шпата В – Р + Г = 16 – 24
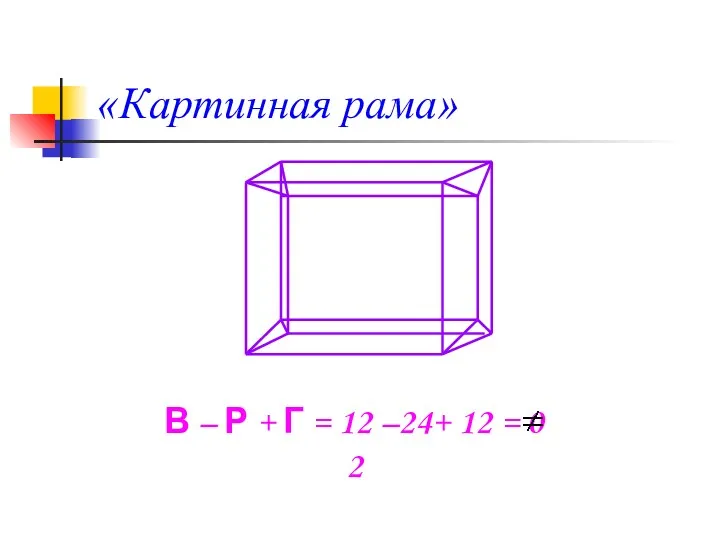
- 8. «Картинная рама» В – Р + Г = 12 –24+ 12 = 0 2
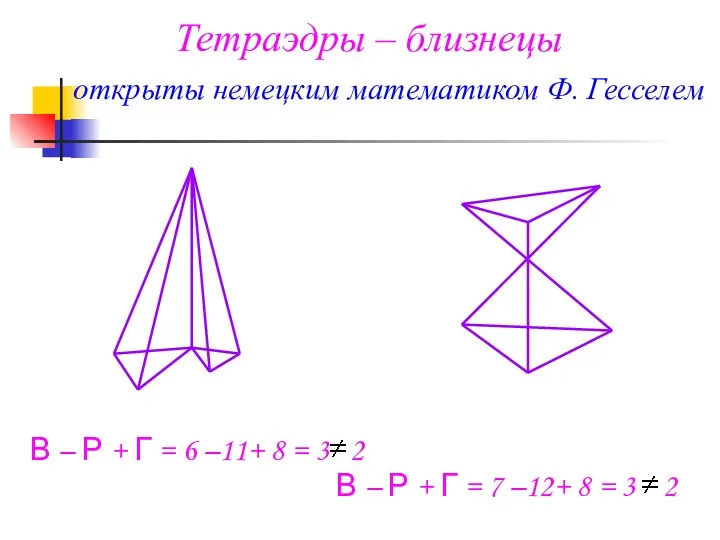
- 9. Тетраэдры – близнецы открыты немецким математиком Ф. Гесселем В – Р + Г = 6 –11+
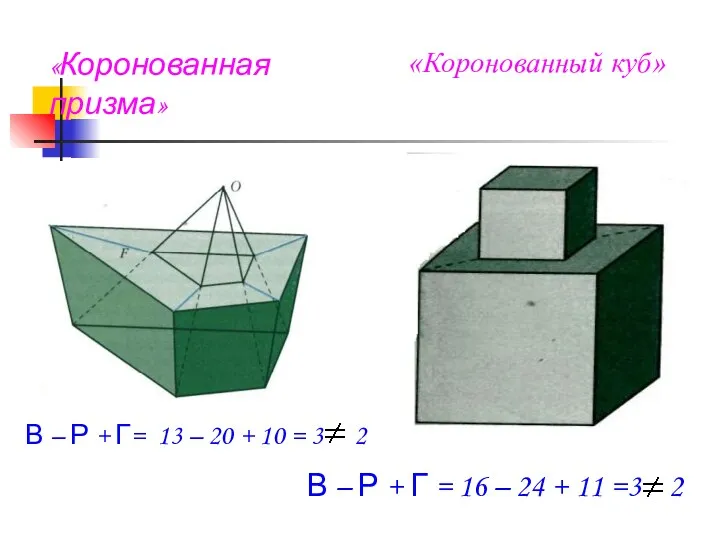
- 10. «Коронованный куб» В – Р + Г = 16 – 24 + 11 =3 2 «Коронованная
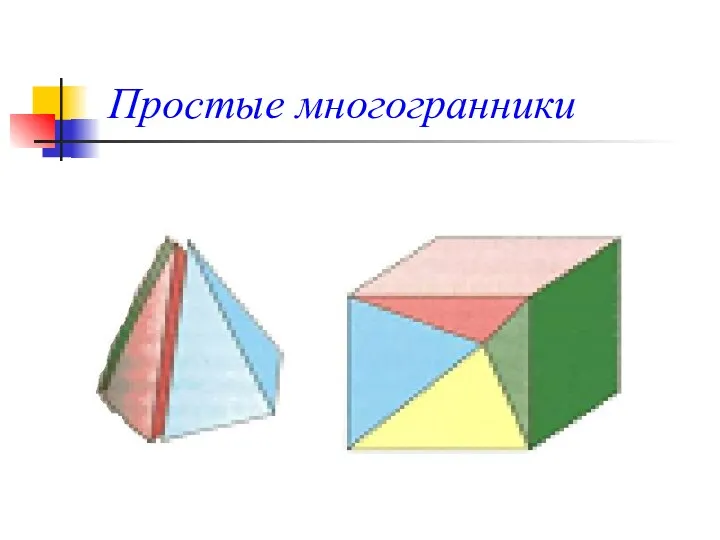
- 11. Простые многогранники
- 12. Кристалл кальцита
- 13. Египетские пирамиды
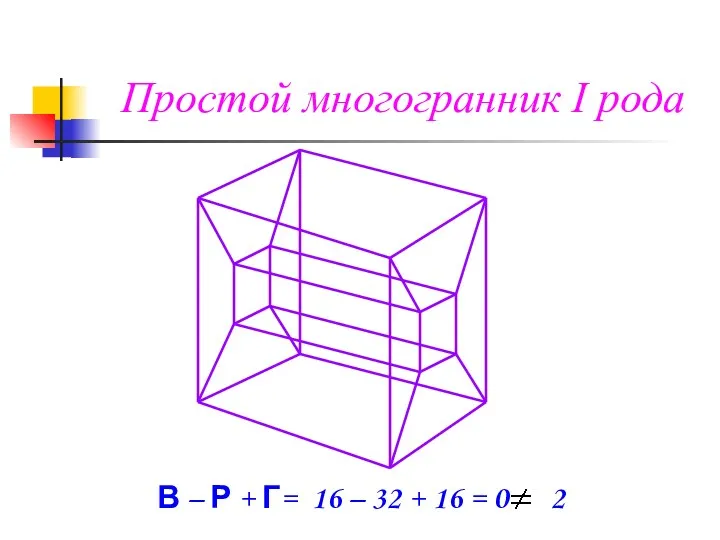
- 16. Простой многогранник I рода В – Р + Г= 16 – 32 + 16 = 0
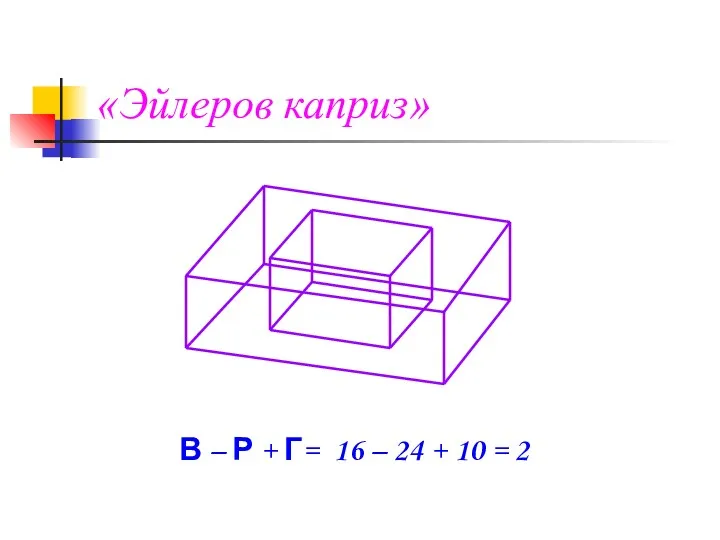
- 17. «Эйлеров каприз» В – Р + Г= 16 – 24 + 10 = 2
- 18. Условия выполнимости соотношения Эйлера в пространстве Для всякого простого многогранника нулевого рода (нет «дыр»), справедливо В
- 19. Теорема Эйлера – первая теорема топологии Топология – раздел геометрии, который изучает свойства фигур, не меняющихся
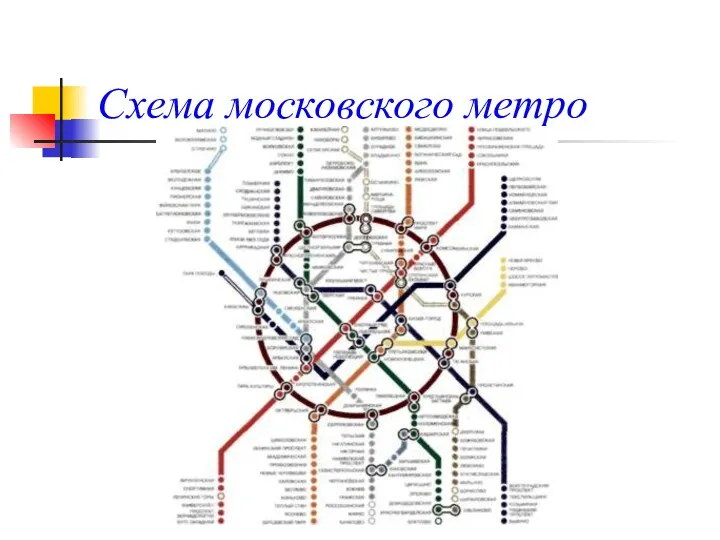
- 20. Схема московского метро
- 21. Генеалогическое древо графа Л.Н.Толстого
- 23. В – Р + Г/ = 1 Г/ = Г - 1 Соотношение Эйлера на плоскости
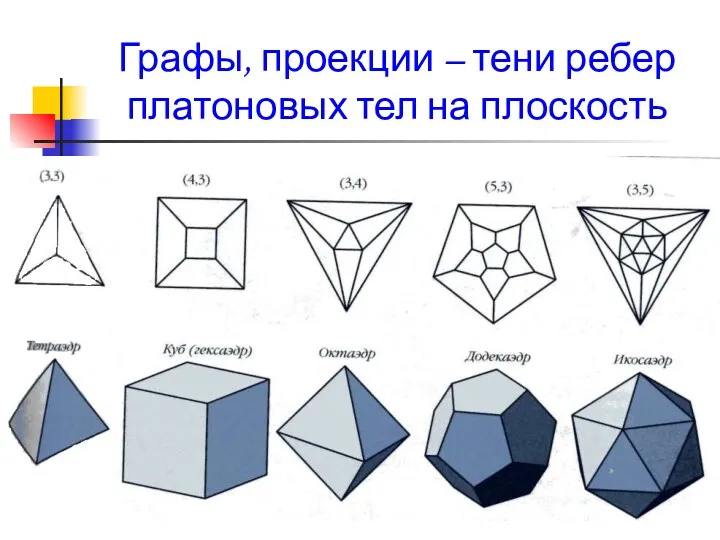
- 24. Графы, проекции – тени ребер платоновых тел на плоскость
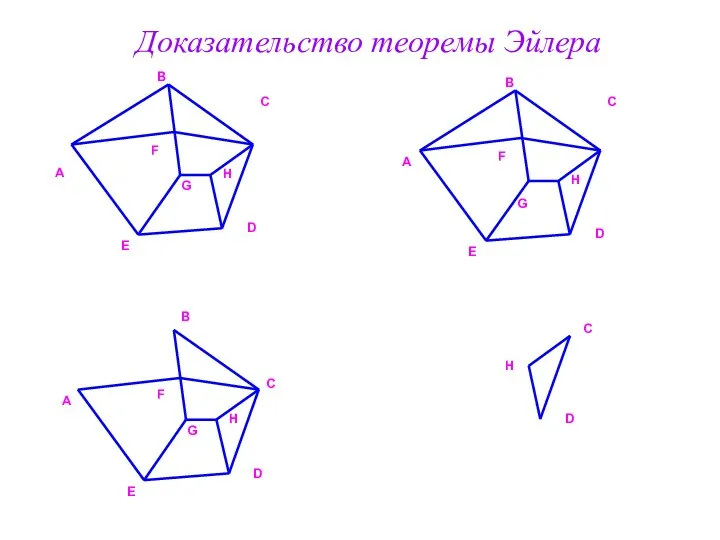
- 25. C C Доказательство теоремы Эйлера
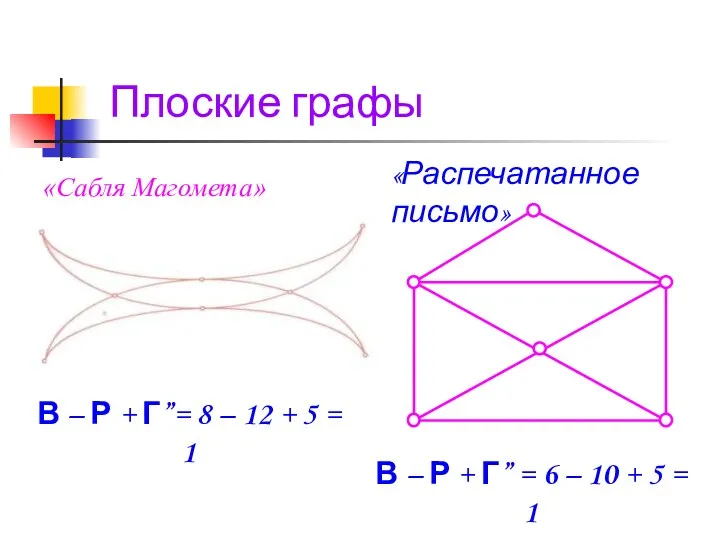
- 26. «Сабля Магомета» В – Р + Г”= 8 – 12 + 5 = 1 «Распечатанное письмо»
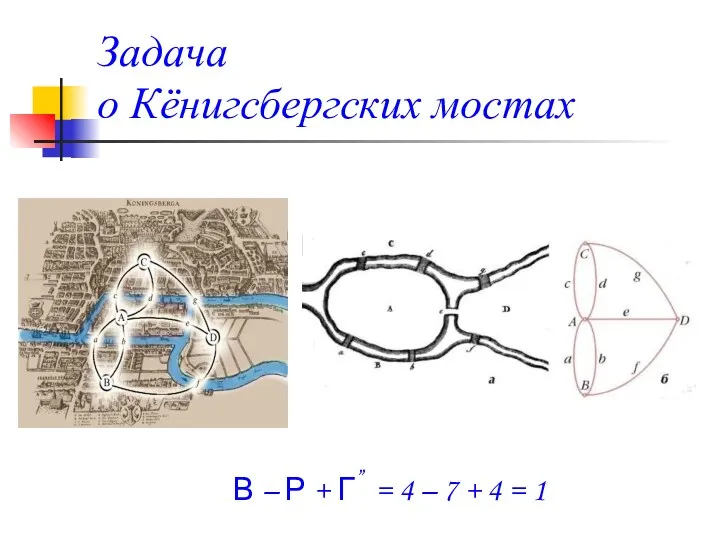
- 27. Задача о Кёнигсбергских мостах В – Р + Г” = 4 – 7 + 4 =
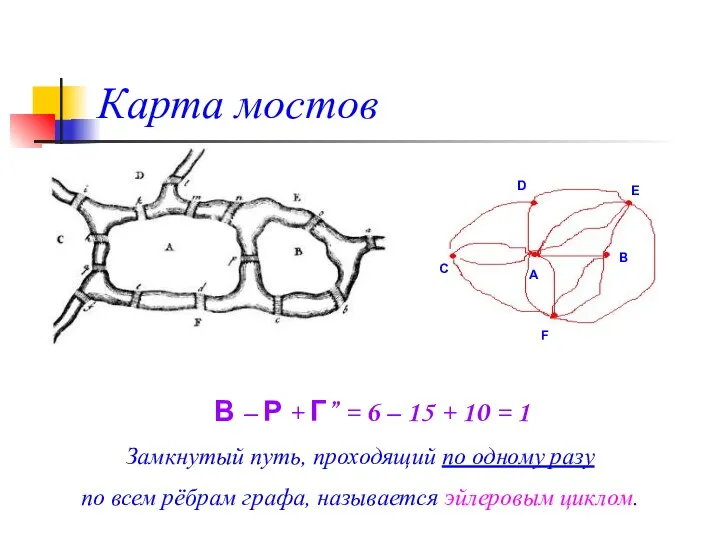
- 28. Карта мостов С D E B A F В – Р + Г” = 6 –
- 29. Условия выполнения эйлерова цикла из любой вершины графа должен существовать путь по его ребрам в любую
- 30. «Домики - колодцы» Можно ли провести непересекающиеся дорожки от каждой избушки к каждому колодцу? В –
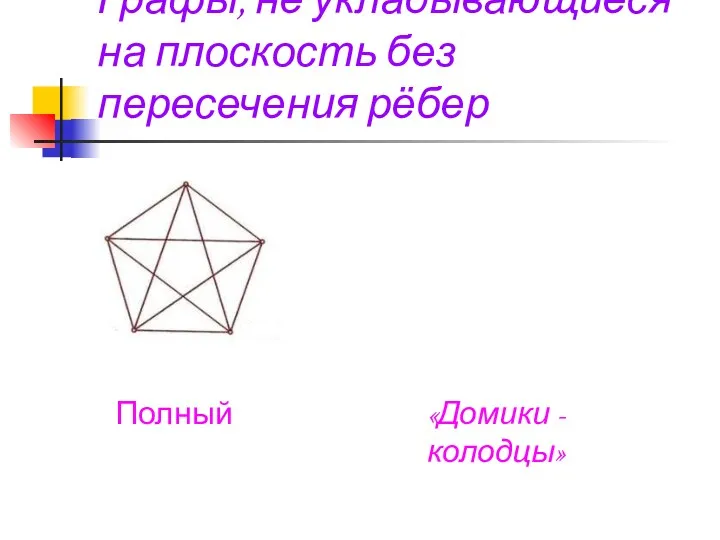
- 31. Графы, не укладывающиеся на плоскость без пересечения рёбер Полный «Домики - колодцы»
- 32. Орграфы - графы, в которых все ребра имеют направления
- 33. Проектная работа
- 34. Задача 1 Из каждой вершины выпуклого многогранника выходит три. Сколько он имеет вершин и граней, если
- 35. Задача 2 Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он
- 36. Задача: Существует ли выпуклый многогранник, у которого количества вершин, ребер и граней – простые числа? Решение:
- 38. Домашнее задание № 315, 317 Творческая работа: составить граф « Моё генеалогическое древо»
- 40. Скачать презентацию


















 Презентация Площадь параллелограмма
Презентация Площадь параллелограмма Урок по теме Свойство параллелограмма. Диск
Урок по теме Свойство параллелограмма. Диск Презентация к уроку Теорема Пифагора
Презентация к уроку Теорема Пифагора Презентация к уроку Простейшие задачи в координатах
Презентация к уроку Простейшие задачи в координатах Презентация + план конспект урока по геометрии Правильный многоугольник в 9 классе.
Презентация + план конспект урока по геометрии Правильный многоугольник в 9 классе. проект по геометрии Правильные паркеты
проект по геометрии Правильные паркеты КроссвордПлощади фигур
КроссвордПлощади фигур Сумма углов треугольника
Сумма углов треугольника Обобщающий урок по теме Четырехугольники
Обобщающий урок по теме Четырехугольники Электронное пособие Треугольники и четырехугольники. Подготовка к ГИА
Электронное пособие Треугольники и четырехугольники. Подготовка к ГИА Презентация к уроку геометрии в 7 классе
Презентация к уроку геометрии в 7 классе Предмет стереометрии. Основные понятия и аксиомы стереометрии
Предмет стереометрии. Основные понятия и аксиомы стереометрии Презентация к уроку геометрии Окружность вписанная в правильный многоугольник для 9 класса
Презентация к уроку геометрии Окружность вписанная в правильный многоугольник для 9 класса Презентация Сказка о четырехугольниках
Презентация Сказка о четырехугольниках Презентация Прямоугольник
Презентация Прямоугольник Решение задач С2 ЕГЭ
Решение задач С2 ЕГЭ Урок одной задачи
Урок одной задачи Урок контроля, оценки и коррекции знаний по теме: Конус. (Учебная презентация по геометрии).
Урок контроля, оценки и коррекции знаний по теме: Конус. (Учебная презентация по геометрии). Кратчайшие расстояния.
Кратчайшие расстояния. 7класс Геометрия Смежные и вертикальные углы
7класс Геометрия Смежные и вертикальные углы Введение. Предмет геометрии. Аксиомы геометрии. Параллельные прямые в пространстве. Параллельность прямой и плоскости. Решение задач по теме: Параллельность прямой и плоскости.
Введение. Предмет геометрии. Аксиомы геометрии. Параллельные прямые в пространстве. Параллельность прямой и плоскости. Решение задач по теме: Параллельность прямой и плоскости. Проект Теорема Пифагора: вчера, сегодня, завтра...
Проект Теорема Пифагора: вчера, сегодня, завтра... физкультминутка
физкультминутка Координаты вектора
Координаты вектора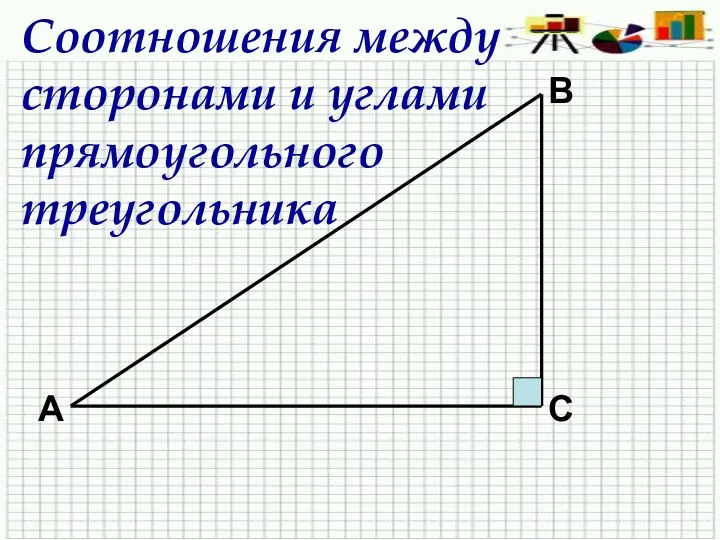 Соотношение между сторонами и углами прямоугольного треугольника.
Соотношение между сторонами и углами прямоугольного треугольника. Урок по теме треугольники в 7 класск по геометрии.
Урок по теме треугольники в 7 класск по геометрии. Урок по геометрии - Вписанные углы
Урок по геометрии - Вписанные углы Конус 11 класс.
Конус 11 класс.