Содержание
- 3. Более плотная фаза (определяющая форму поверхности) называется адсорбентым (обычно адсорбент это твердая или жидкая фаза) Вещество
- 4. Адсорбция может происходить на любой поверхности раздела между фазами. В зависимости от агрегатного состояния смежных фаз
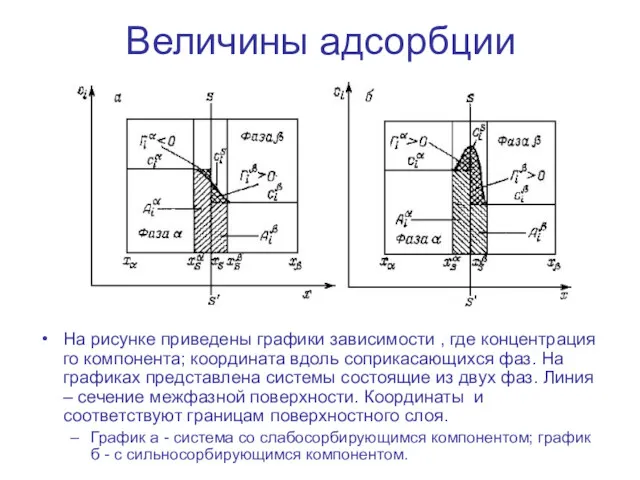
- 11. Величины адсорбции На рисунке приведены графики зависимости , где концентрация го компонента; координата вдоль соприкасающихся фаз.
- 12. Рассмотрим объединенное уравнение I и II законов термодинамики в открытой системе с учетом энергии поверхностного натяжения
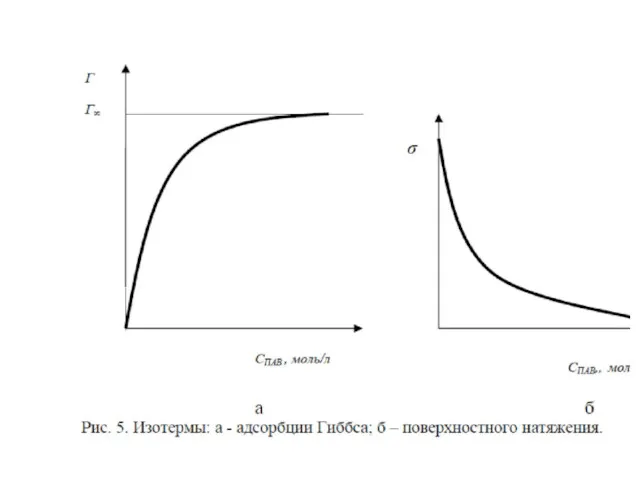
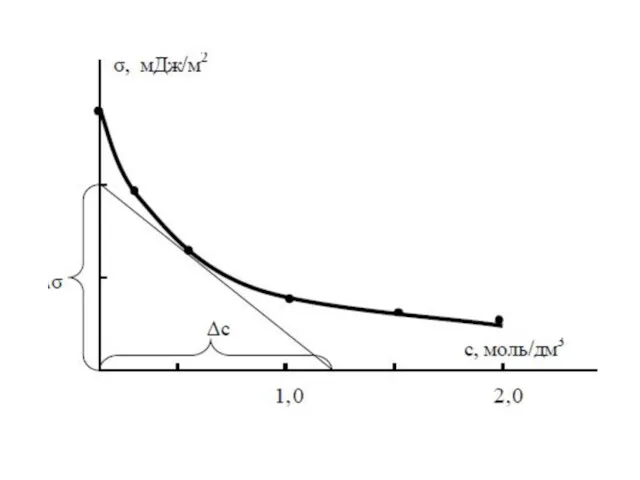
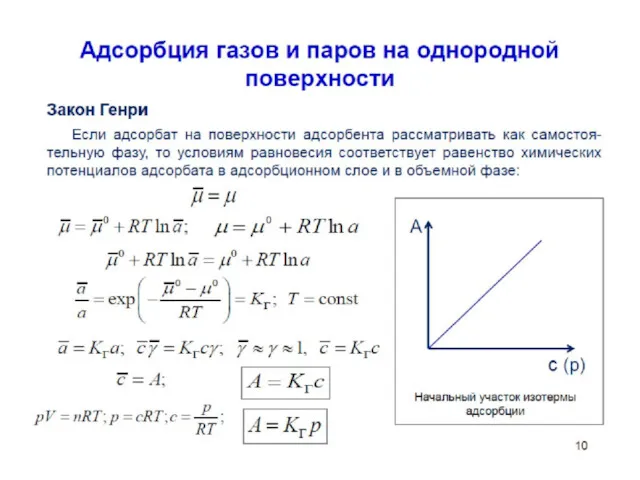
- 13. В случае получим выражение Учитывая, что Получим фундаментальное адсорбционное уравнение Гиббса: Зависимость поверхностного натяжения от адсорбции
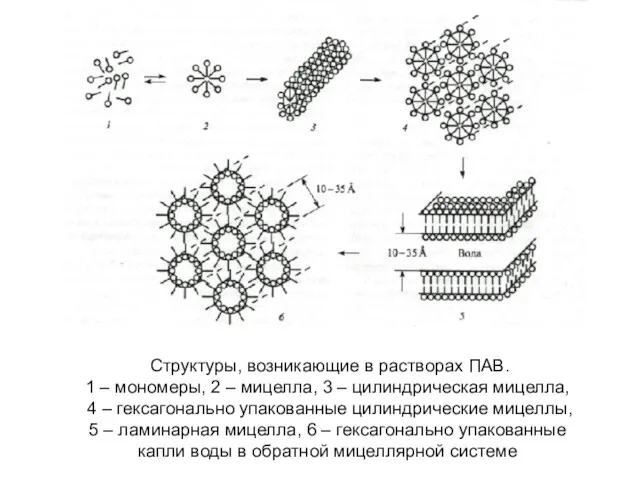
- 27. Структуры, возникающие в растворах ПАВ. 1 – мономеры, 2 – мицелла, 3 – цилиндрическая мицелла, 4
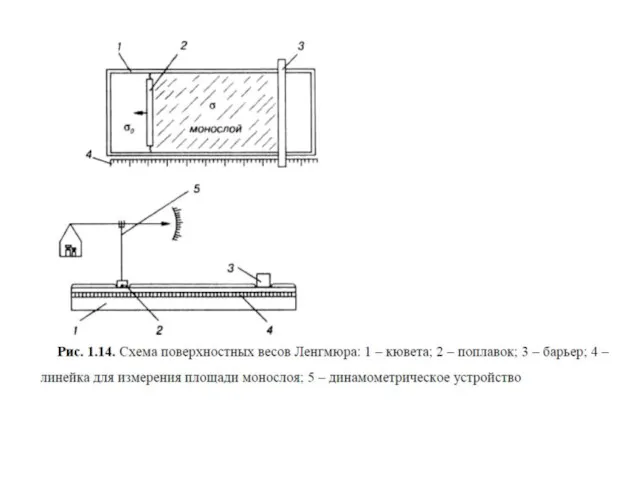
- 28. Весы Ленгмюра
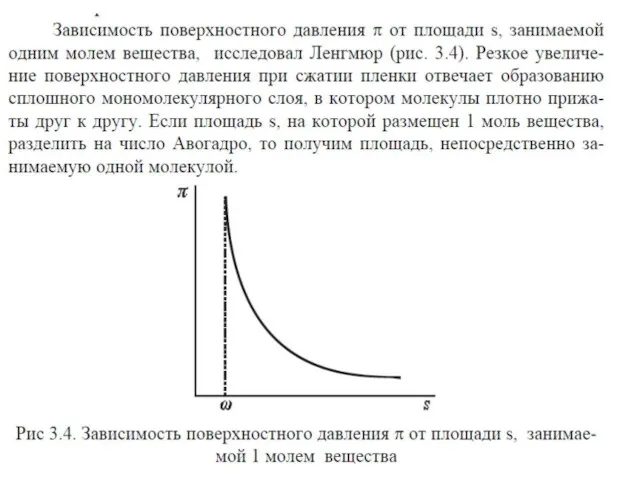
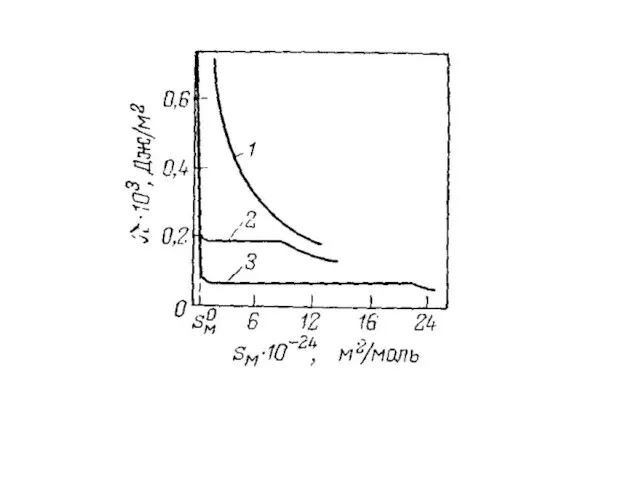
- 32. При адсорбции или растекании вещества на поверхности образуется поверхностная (адсорбционная) пленка этого вещества. Уравнение изотермы поверхностного
- 33. Введем обозначения: или если разделить на число Авогадро площадь приходящаяся в поверхностном слое на одну молекулу
- 34. В ряде случаев можно применять уравнение аналогичное уравнению Ван-дер-Ваальса В котором константа а характеризует силы взаимного
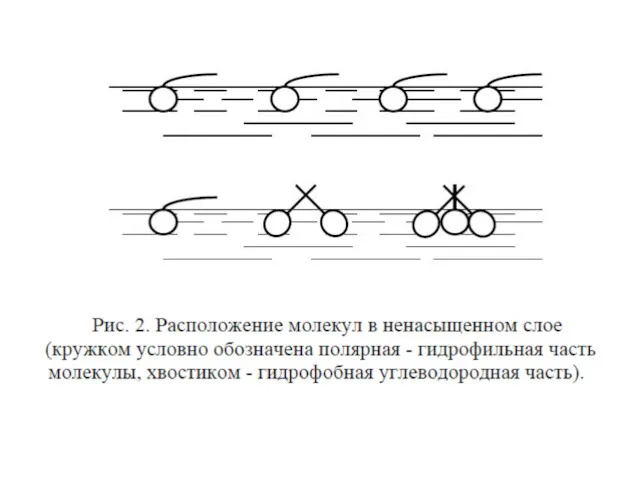
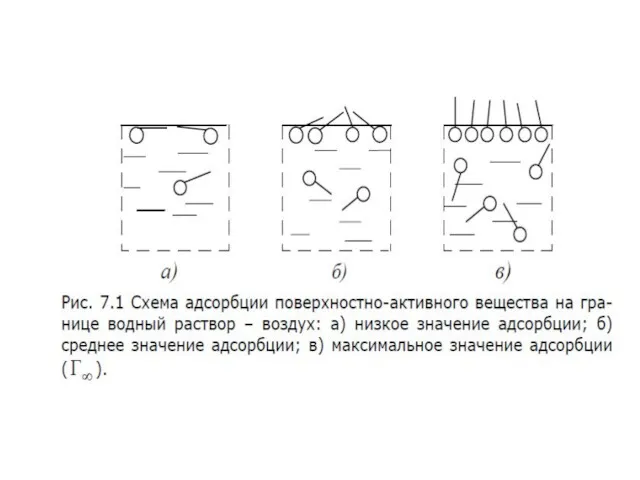
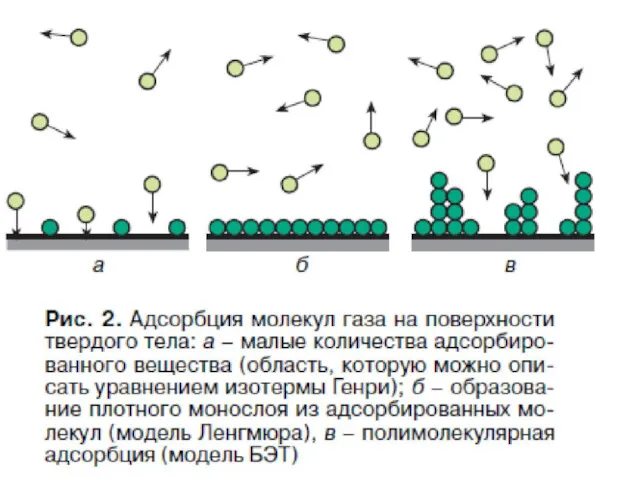
- 35. При небольшой концентрации амфифильного соединения мономолекулярный слой на поверхности не является сплошным. Молекулы практически не взаимодействуют
- 36. При уменьшении площади с помощью плавучего барьера молекулы сблизятся, но будут все еще хаотически ориентированы. Такую
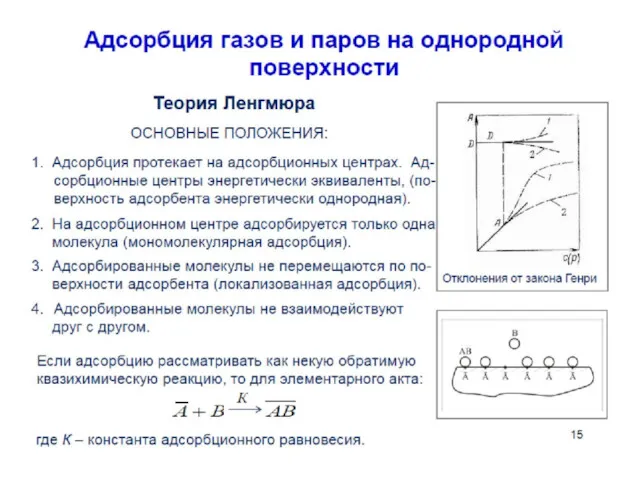
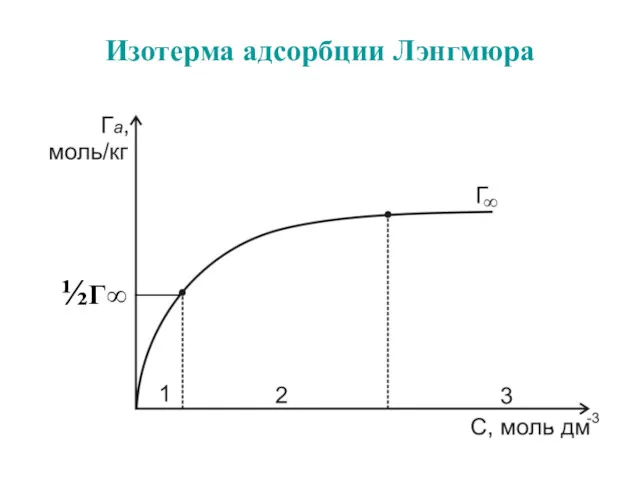
- 48. Изотерма адсорбции Лэнгмюра ½Г∞
- 49. Уравнение Ленгмюра в линейной форме
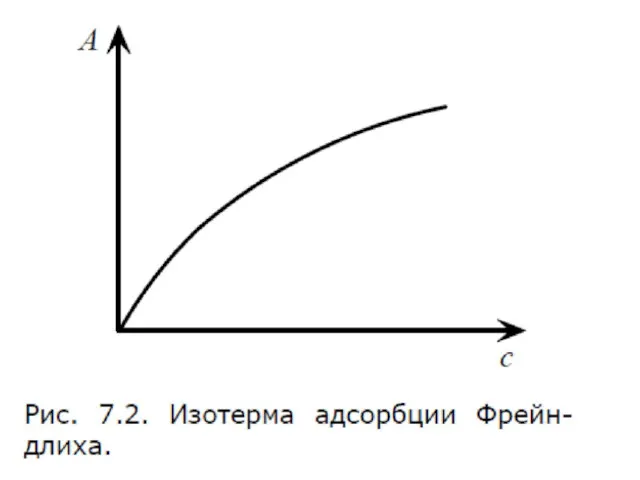
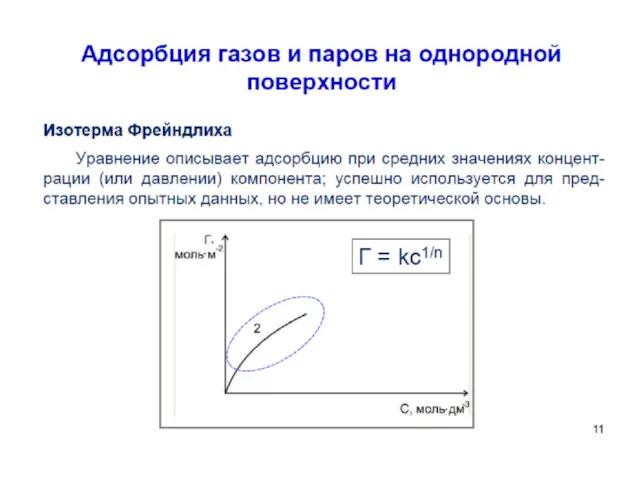
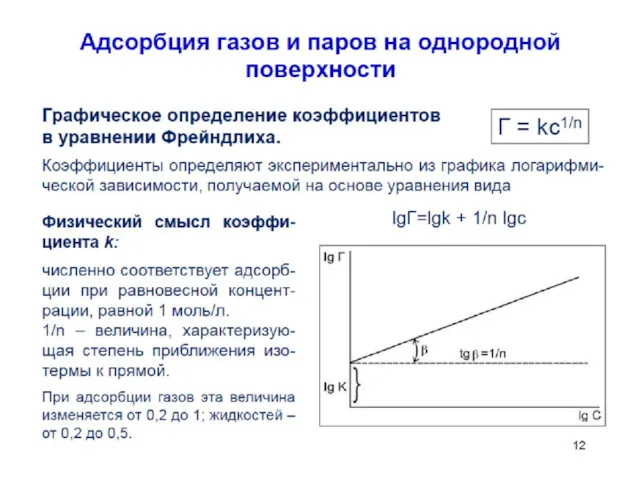
- 54. Уравнение Фрейндлиха. К, 1/n – эмпирические постоянные, т.е. на основе экспериментальных данных; С – равновесная концентрация
- 57. Уравнение Фрейндлиха. К, 1/n – эмпирические постоянные, т.е. на основе экспериментальных данных; С – равновесная концентрация
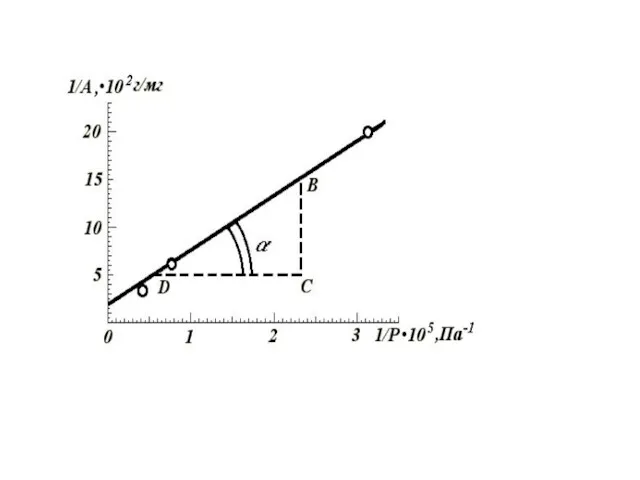
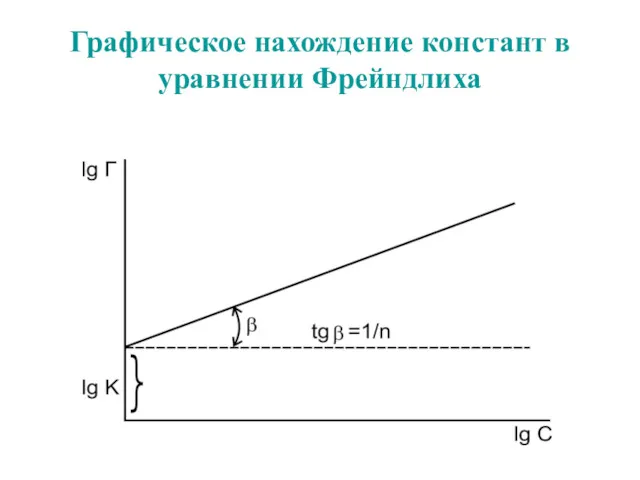
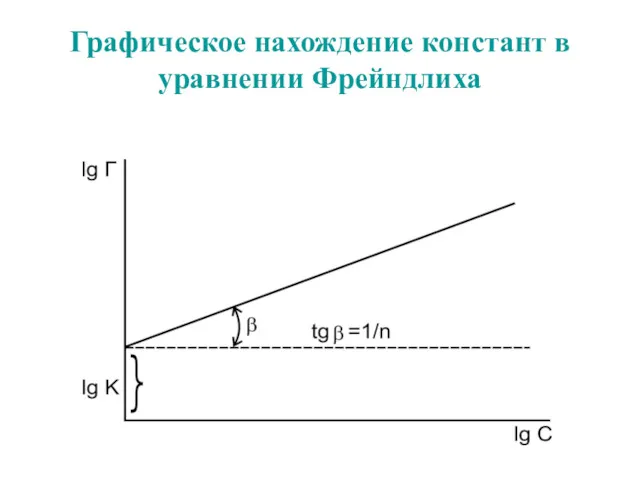
- 59. Графическое нахождение констант в уравнении Фрейндлиха
- 62. Графическое нахождение констант в уравнении Фрейндлиха
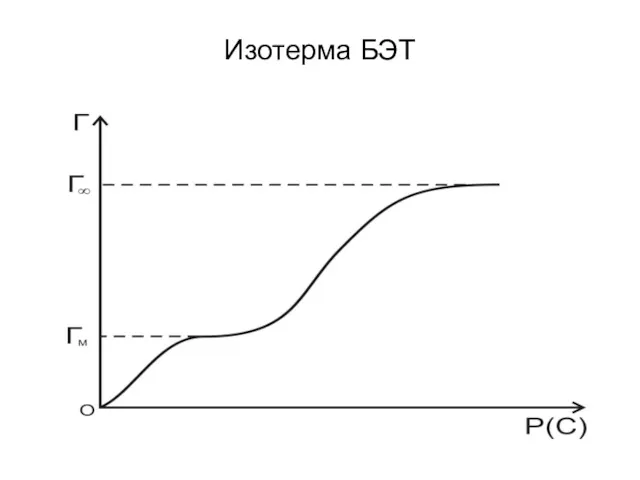
- 75. Изотерма БЭТ
- 77. С уменьшением давления уравнение БЭТ переходит в уравнение мономолекулярной адсорбции Ленгмюра. При
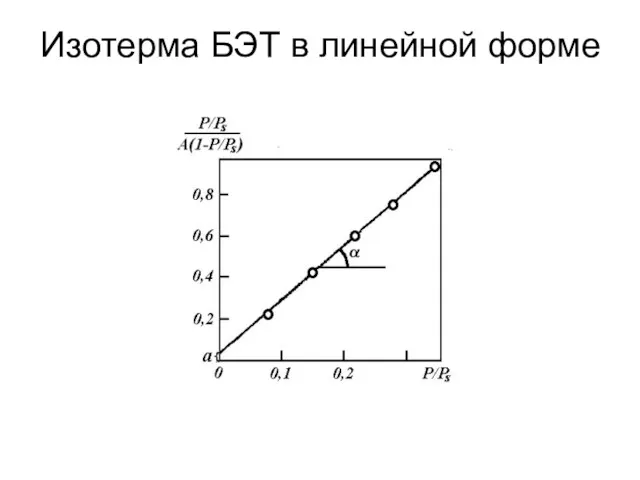
- 78. Изотерма БЭТ в линейной форме
- 83. Скачать презентацию




















































 Соляная кислота и её соли
Соляная кислота и её соли Растворы
Растворы Органическая химия. Этапы развития органической химии
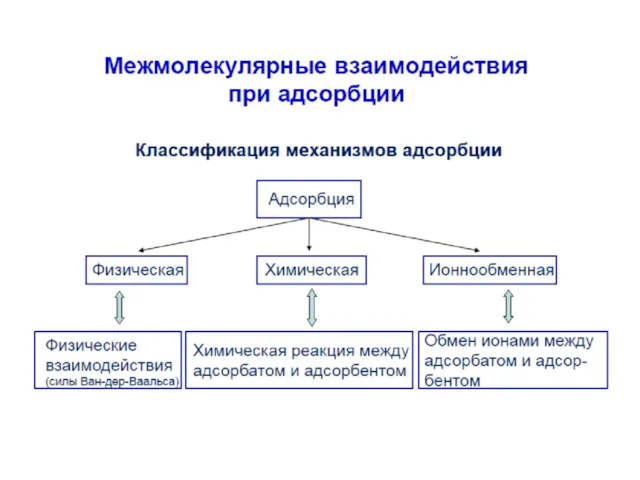
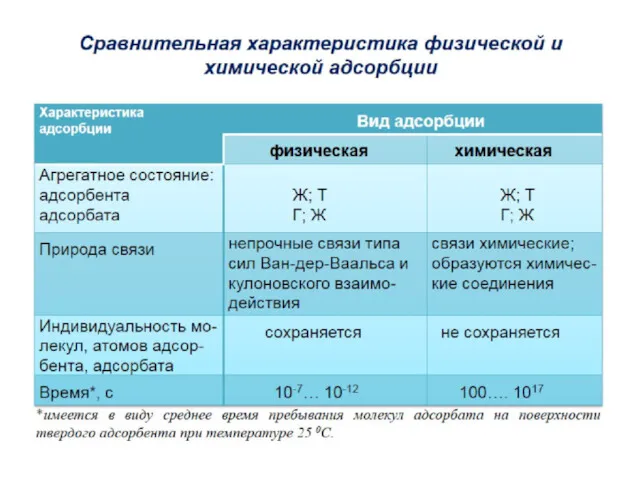
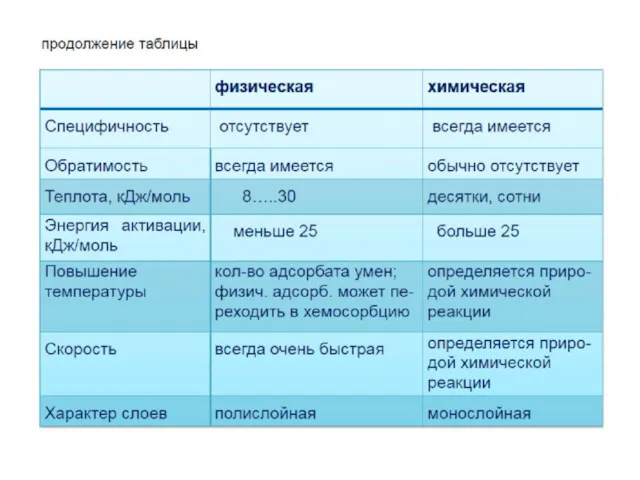
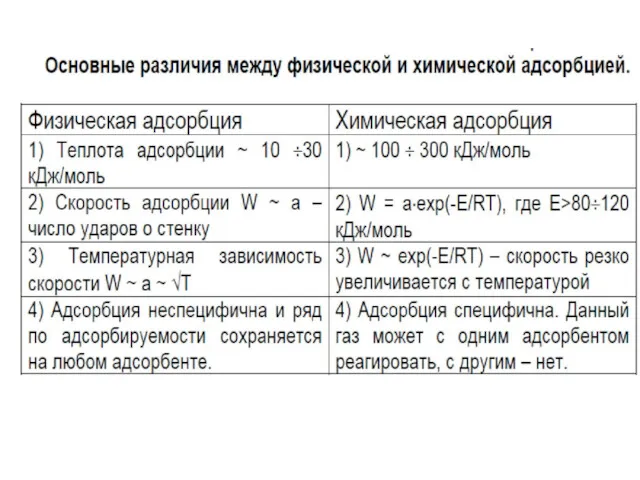
Органическая химия. Этапы развития органической химии Поверхностные явления. Адсорбция
Поверхностные явления. Адсорбция Минеральные удобрения
Минеральные удобрения Химическая связь
Химическая связь Альдегіди і кетони аліфатичного ряду. Альдегіди і кетони ароматичного ряду
Альдегіди і кетони аліфатичного ряду. Альдегіди і кетони ароматичного ряду Фенол и его свойства
Фенол и его свойства Тема 1. Обработка вооружения, техники и обмундирования. Дегазирующие, дезактивирующие и дезинфицирующие вещества и растворы
Тема 1. Обработка вооружения, техники и обмундирования. Дегазирующие, дезактивирующие и дезинфицирующие вещества и растворы Соединения химических элементов
Соединения химических элементов Решение задач по теме: «Электролиз»
Решение задач по теме: «Электролиз» Химическая посуда и ее значение (1)
Химическая посуда и ее значение (1) Классификация неорганических веществ
Классификация неорганических веществ Углерод, как химический элемент и простое вещество
Углерод, как химический элемент и простое вещество АТФ Аденозинтрифосфат
АТФ Аденозинтрифосфат Оксиды, свойства и способы получения
Оксиды, свойства и способы получения Общие сведения о месторождениях полезных ископаемых
Общие сведения о месторождениях полезных ископаемых Золото Au (Аурум)
Золото Au (Аурум) Применение уксусной кислоты
Применение уксусной кислоты Определение качественного состава минеральных вод
Определение качественного состава минеральных вод Химическое равновесие. Азот и Фосфор. 9 класс
Химическое равновесие. Азот и Фосфор. 9 класс Корбонаттар көмір қышқылынның тұздары
Корбонаттар көмір қышқылынның тұздары Химическая промышленность
Химическая промышленность Алюминий. Строение
Алюминий. Строение Свойства металлов
Свойства металлов Коррозия металлов
Коррозия металлов Механизм реакции
Механизм реакции Основные виды химических связей
Основные виды химических связей