Содержание
- 2. ДУ с разделяющимися переменными 2. Однородные уравнения Линейные уравнения Уравнения Бернулли Уравнения в полных дифференциалах
- 3. ДУ с разделяющимися переменными 2. Однородные уравнения Линейные уравнения Уравнения Бернулли Уравнения в полных дифференциалах
- 4. ДУ с разделяющимися переменными 2. Однородные уравнения Линейные уравнения Уравнения Бернулли Уравнения в полных дифференциалах
- 5. Замечание. ДУ может быть линейным или уравнением Бернулли не только относительно y, но и относительно x.
- 6. ДУ с разделяющимися переменными 2. Однородные уравнения Линейные уравнения Уравнения Бернулли Уравнения в полных дифференциалах
- 7. ДУ с разделяющимися переменными 2. Однородные уравнения Линейные уравнения Уравнения Бернулли Уравнения в полных дифференциалах
- 8. РЕШЕНИЕ ЗАДАЧ
- 9. Пример 9 Решить ДУ
- 10. - уравнение Бернулли Пример 10 Решить ДУ
- 11. 5
- 12. Пример 12 Решить ДУ
- 13. Пример 13 Решить ДУ
- 14. Выполнение критерия означает, что существует некая функция , для которой Решить ДУ Пример
- 15. Из первого равенства, интегрируя по х Из второго равенства, интегрируя по у Искомая функция +(недостающие слагаемые
- 16. Здесь Проверяем критерий: Частные производные равны. Данное уравнение есть уравнение в полных дифференциалах. Нужно найти функцию
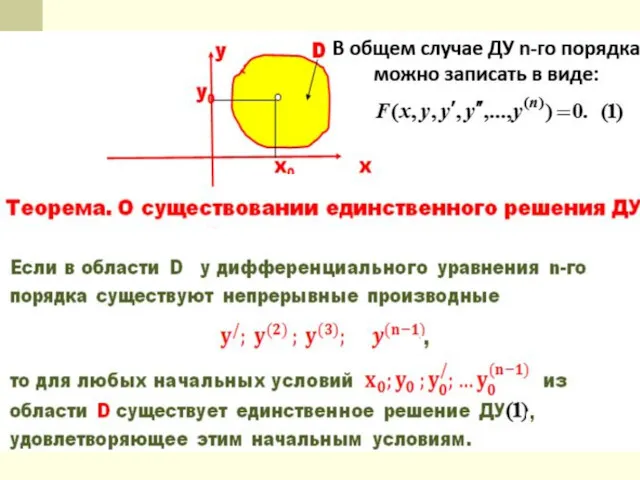
- 18. Уравнения высших порядков ДУ 2-го порядка называется уравнение, которое содержит независимую переменную х искомую функцию у
- 19. З а д а ч а К о ш и для уравнения состоит в нахождении частного
- 20. УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА Тип I. Уравнения вида Решение находится путем последовательного интегрирования. общее решение уравнения
- 21. Пример
- 22. Пример
- 23. Тип II. После подстановки получаем уравнение первого порядка Разделяем переменные Пример. Решить ДУ 23
- 24. Тип III. Пример. Решить ДУ 24
- 25. Решить задачу Коши Так как Частное решение Так как Пример. 25
- 26. Комплексные числа Комплексным числом Z называется выражение вида где и – действительные числа, а – мнимая
- 27. Два комплексных числа называются комплексно сопряженными. Справедливо равенство
- 28. Пример. 1. Вычислить 2. Решить уравнение 3. Решить уравнение Решение. 1.
- 29. 2. 3.
- 30. Функции y1(x), y2(x), … , yn(x) линейно независимы на I=(a,b), если существуют действительные числа α1 ,
- 31. ТЕОРЕМА. Для того, чтобы функции y1(x) , y2(x) , … , yn(x) –были линейно независимы на
- 32. Пример. Найти определитель Вронского системы функций на указанном интервале:
- 34. Скачать презентацию






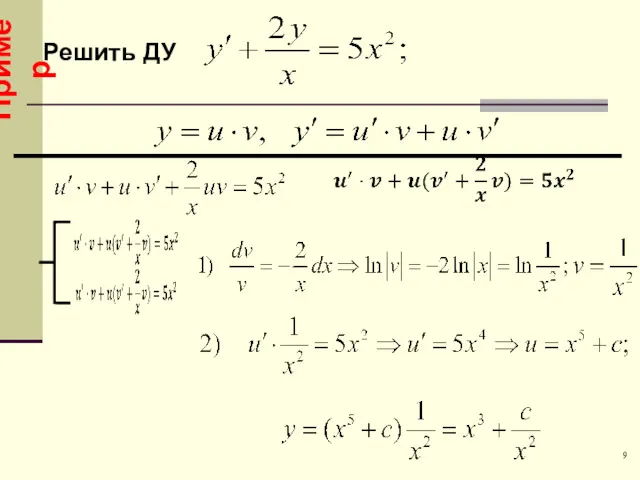

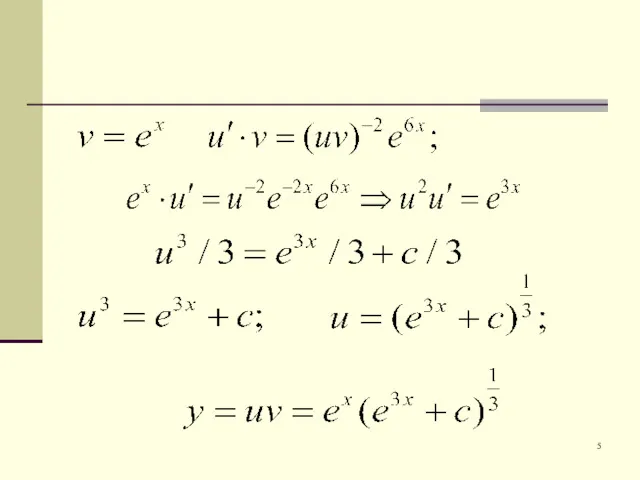
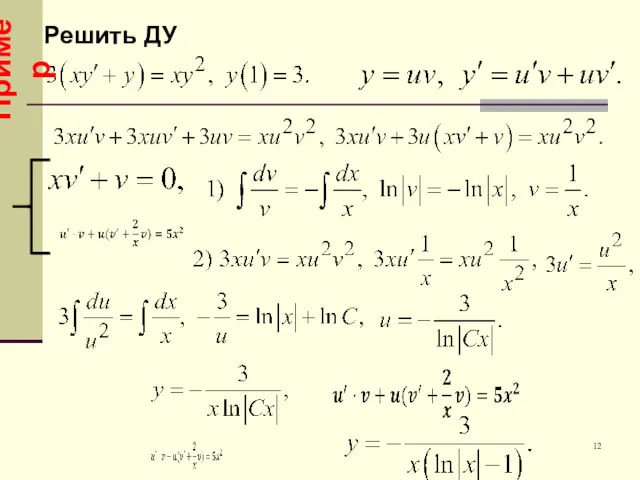
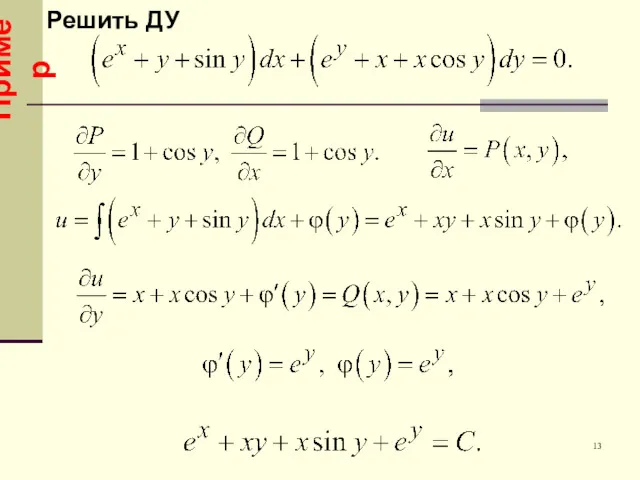






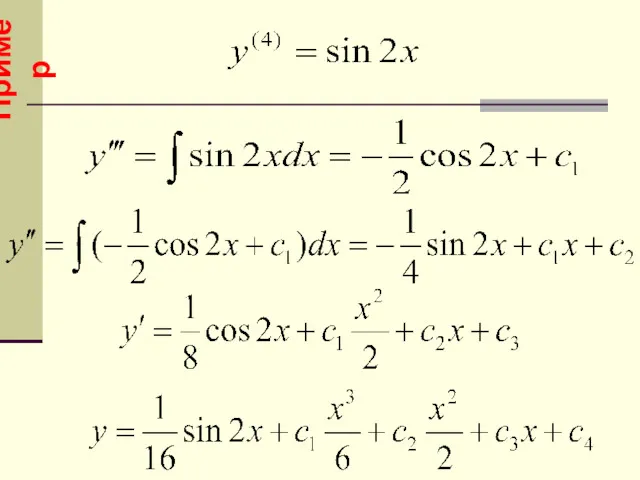
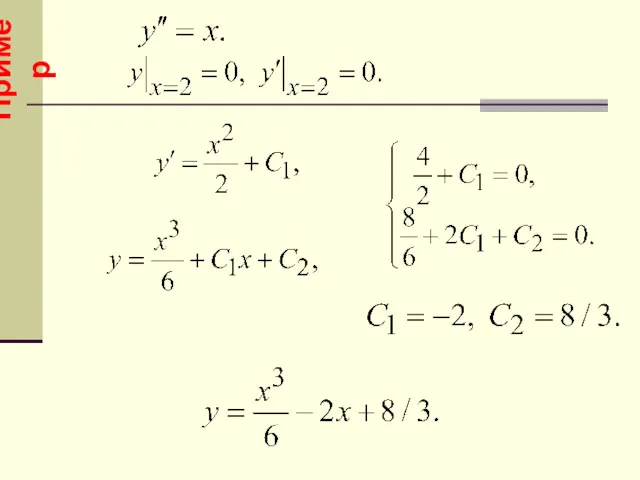

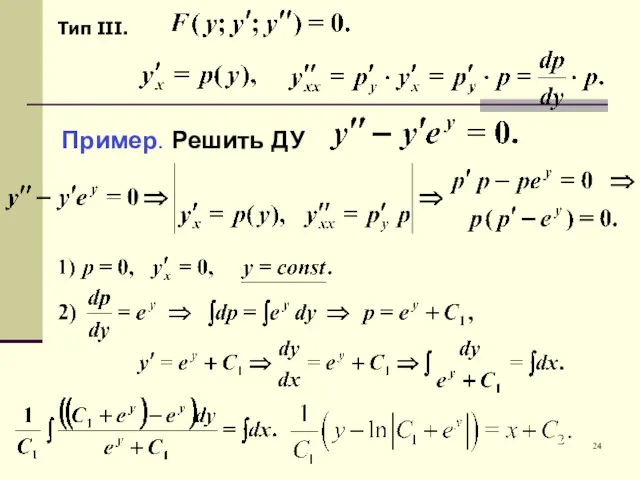




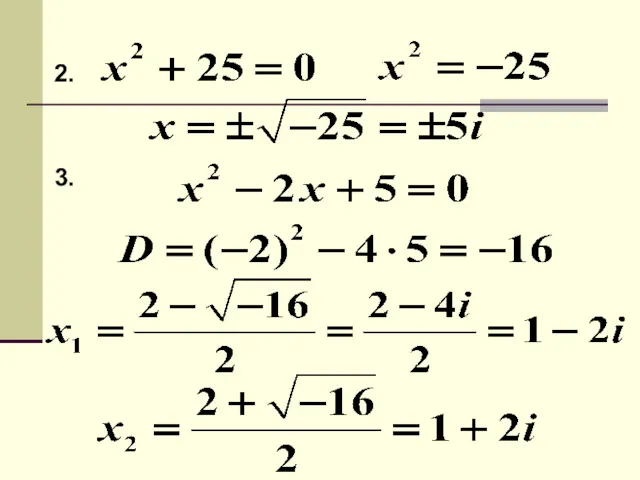



 Обобщающий урок по теме параллелограмм 8 класс
Обобщающий урок по теме параллелограмм 8 класс Тетраэдр. Сечение тетраэдра
Тетраэдр. Сечение тетраэдра Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса Презентация по математике по теме Логарифм для 10-11 класса
Презентация по математике по теме Логарифм для 10-11 класса Обчислення на основі нумерації. Складання задач різних типів за малюнками та частиною умови. Урок №111
Обчислення на основі нумерації. Складання задач різних типів за малюнками та частиною умови. Урок №111 Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел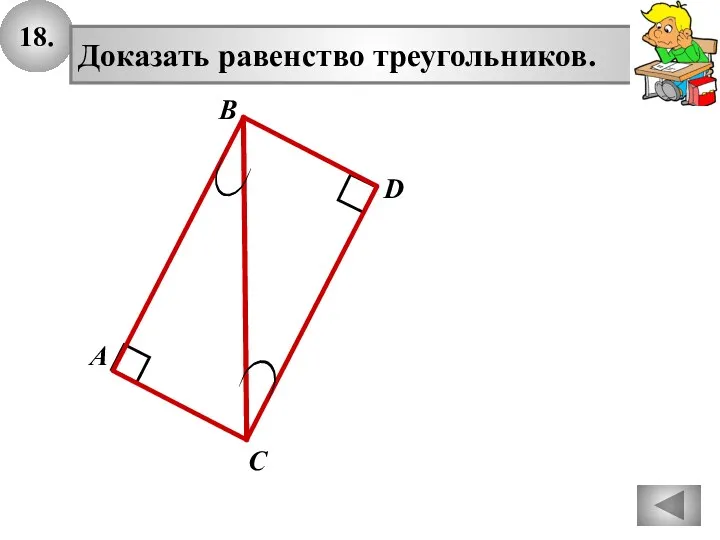 Прямоугольные треугольники
Прямоугольные треугольники Что такое умножение
Что такое умножение Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе
Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе Выражения, равенства, неравенства, уравнения .
Выражения, равенства, неравенства, уравнения . Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1)
Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1) Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций нескольких переменных Сумма и разность дробей
Сумма и разность дробей Математические модели
Математические модели Длина окружности и площадь круга
Длина окружности и площадь круга Логарифмическая функция, ее график и свойства
Логарифмическая функция, ее график и свойства Разложение на множители суммы и разности кубов
Разложение на множители суммы и разности кубов Метрические задачи
Метрические задачи Основные сведения теории вероятностей. Надежность технических систем и техногенный риск
Основные сведения теории вероятностей. Надежность технических систем и техногенный риск Сложение однозначных чисел с переходом через десяток вида + 8, +9
Сложение однозначных чисел с переходом через десяток вида + 8, +9 Решение системы способом подстановки. 7 класс
Решение системы способом подстановки. 7 класс Решение систем линейных уравнений. 7 класс
Решение систем линейных уравнений. 7 класс Презентация Метр 2 класс
Презентация Метр 2 класс Графический метод решения уравн
Графический метод решения уравн Вычислительная математика. Лекция 5. Системы линейных алгебраических уравнений
Вычислительная математика. Лекция 5. Системы линейных алгебраических уравнений Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс Презентация Устный счёт 2 класс 1 четверть № 3
Презентация Устный счёт 2 класс 1 четверть № 3