Содержание
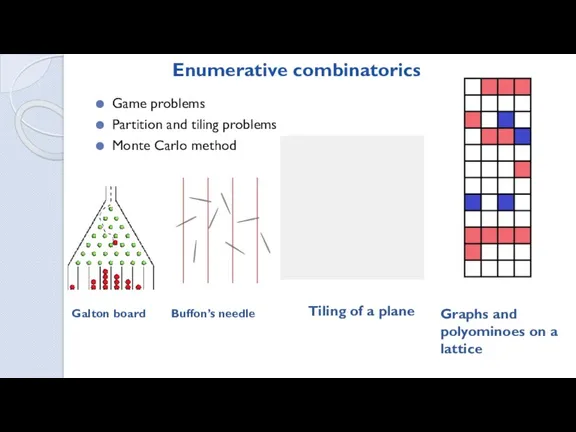
- 2. Enumerative combinatorics Game problems Partition and tiling problems Monte Carlo method Buffon’s needle Galton board Tiling
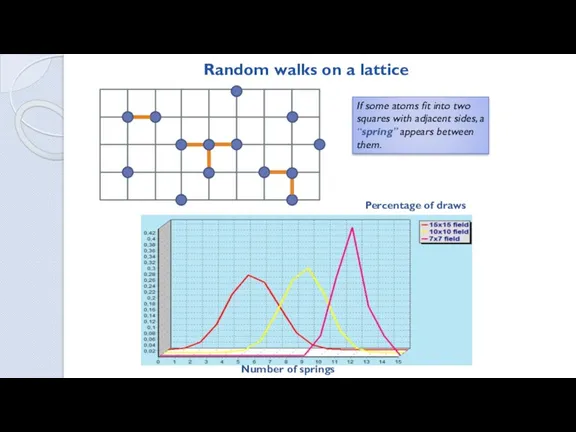
- 3. Random walks on a lattice If some atoms fit into two squares with adjacent sides, a
- 4. Example: n1=2, n2=4, n3=2, n4=3 Generalize the results for: three-dimensional space: d=3 lattice with holes surface
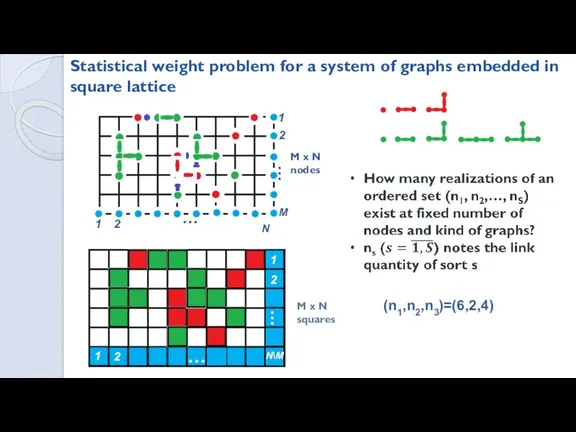
- 5. Statistical weight problem for a system of graphs embedded in square lattice 1 2 … N
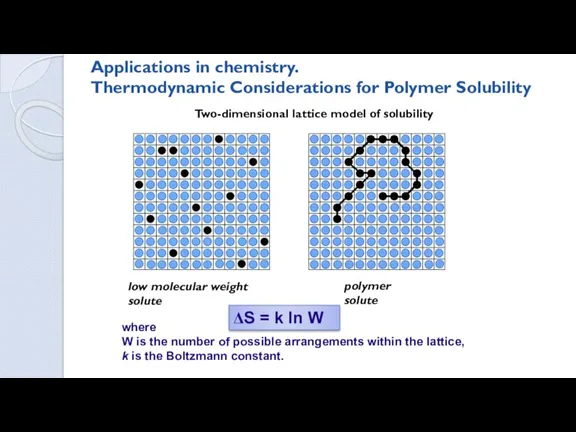
- 6. Applications in chemistry. Thermodynamic Considerations for Polymer Solubility where W is the number of possible arrangements
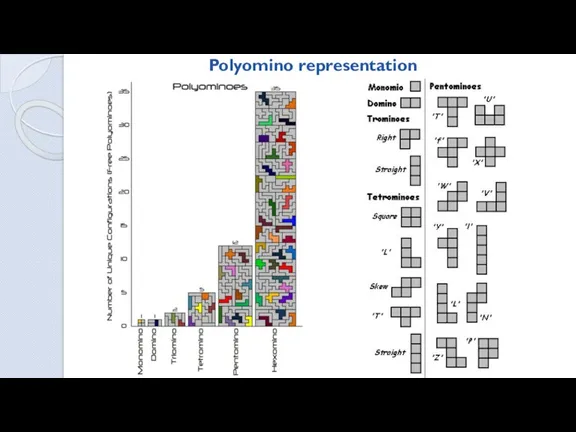
- 7. Polyomino representation
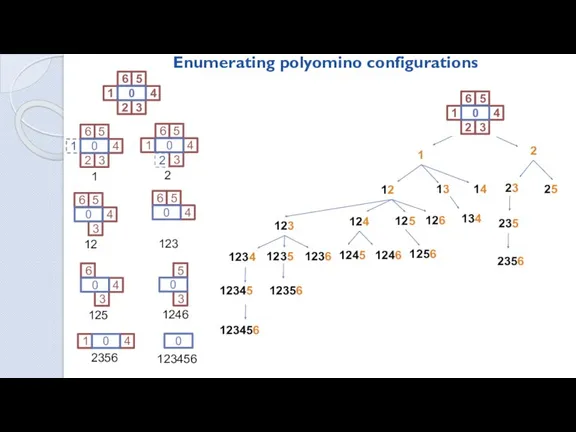
- 8. 1 2 12 13 14 123 124 1234 1235 1236 12345 12356 123456 1245 1246 125
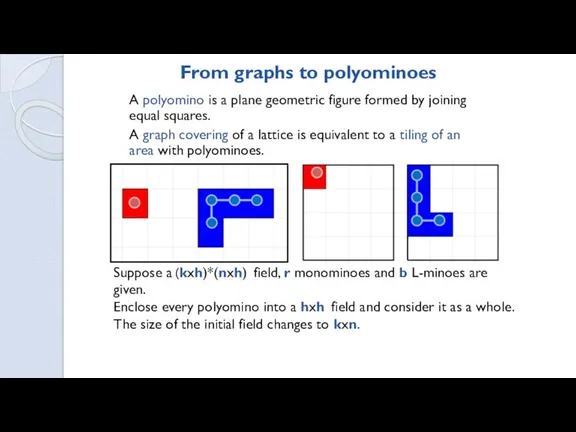
- 9. From graphs to polyominoes A polyomino is a plane geometric figure formed by joining equal squares.
- 10. . Polyomino adjacency cases hxh field Calculating the number of possible adjacencies (P) c is a
- 11. Direct method of counting partitions Suppose a MxN stripe and a set of polyominoes are given.
- 12. L-minoes and dominoes on a 2xn stripe = =
- 13. Calculation of infinite sums
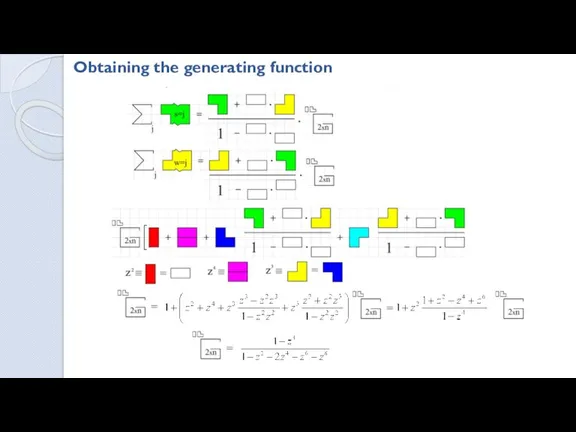
- 14. Obtaining the generating function
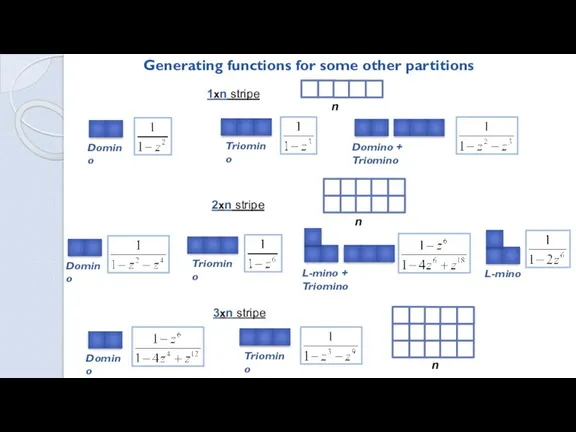
- 15. Generating functions for some other partitions 1xn stripe Domino Triomino Domino + Triomino 2xn stripe Domino
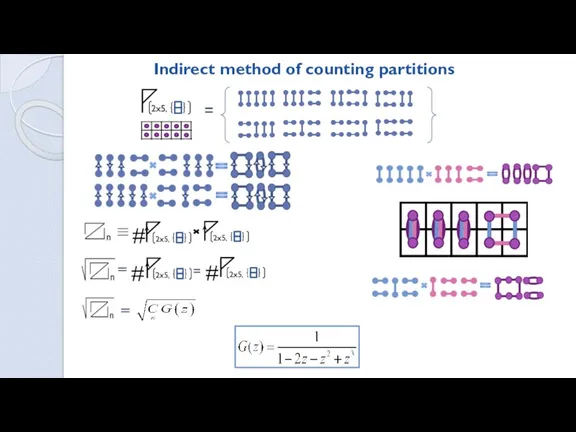
- 16. Indirect method of counting partitions # # #
- 17. . . . n-1 n . . . n-2 n j . . . n-j j
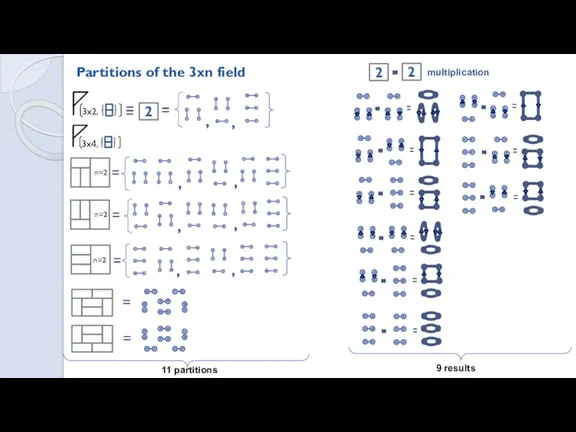
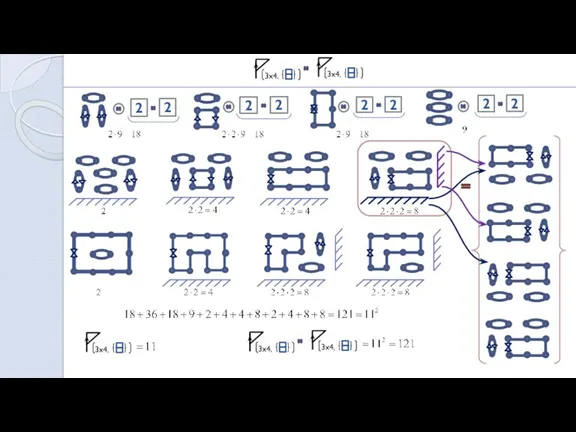
- 18. Partitions of the 3xn field 11 partitions 9 results 2 2 2 , , multiplication
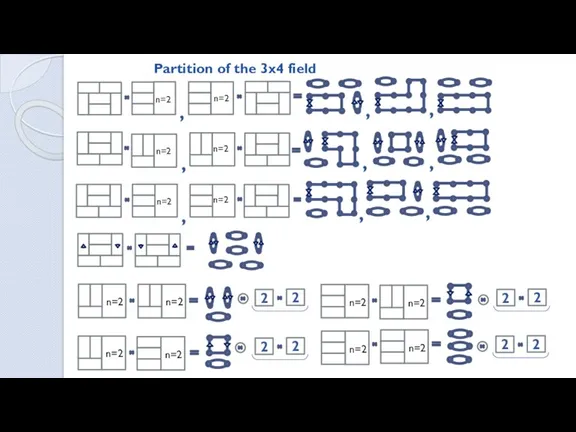
- 19. n=2 n=2 n=2 n=2 , , , , , , , , , Partition of the
- 20. 2 2
- 21. Kasteleyn’s formula for the number of perfect matchings in a planar graph G Pfaffian method Pfaffian
- 22. 4 binary operations: 3 unary operations: – without forming a spring – with forming a horizontal
- 23. Properties of unary and binary operations
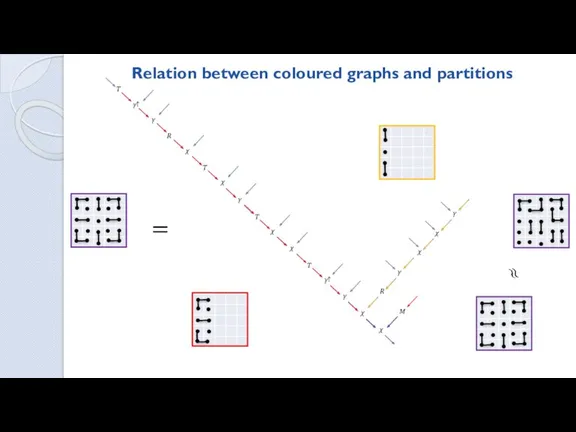
- 25. Relation between coloured graphs and partitions T γ↑ γ R χ T χ γ γ χ
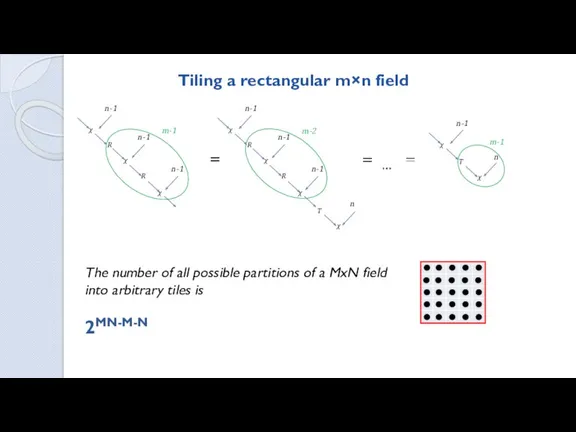
- 26. Tiling a rectangular m×n field χ R χ R χ n-1 n-1 n-1 m-1 χ R
- 27. Partitions of a MxN field into arbitrary tiles M N M-1 N-1
- 28. Aims & perspectives Algebraization of the tiling problem Finding a method applicable to the whole class
- 29. Connection with modern art Robert Delaunay. City. 1910 Georges Braque. Mandora.1909-10 Pablo Picasso. Harlequin with Violin.
- 30. Evolution of primitive geometric shapes Searching for rhythmical structures – investigating adjacent/non-adjacent squares on a lattice
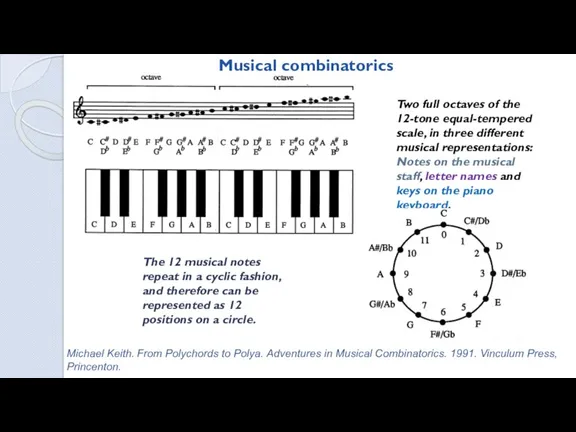
- 31. Musical combinatorics Two full octaves of the 12-tone equal-tempered scale, in three different musical representations: Notes
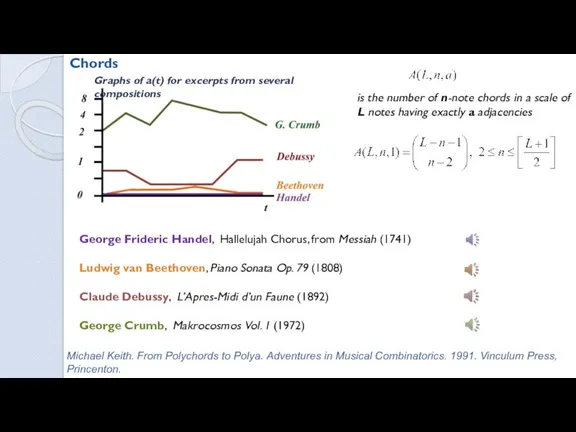
- 32. George Frideric Handel, Hallelujah Chorus, from Messiah (1741) Ludwig van Beethoven, Piano Sonata Op. 79 (1808)
- 33. Lattice model in music 1/4 The lattice you have seen at the beginning represents a fragment
- 34. Enumerative combinatorics Game problems Partition and tiling problems Monte Carlo method Buffon’s needle Galton board Tiling
- 36. Скачать презентацию














 Ортогональный композиционный план Бокса
Ортогональный композиционный план Бокса Процент төшенчәсе белән танышу. Процентлар табу
Процент төшенчәсе белән танышу. Процентлар табу Письменное сложение трехзначных чисел
Письменное сложение трехзначных чисел Основы метрологии, стандартизации, сертификации и управление качеством
Основы метрологии, стандартизации, сертификации и управление качеством Биография пустого места, или Удивительная история нуля
Биография пустого места, или Удивительная история нуля Многогранники. 10-11 класс
Многогранники. 10-11 класс презентация к уроку математики 6 класс виленкин
презентация к уроку математики 6 класс виленкин Урок по математике Единицы длины. Километр. 4 класс
Урок по математике Единицы длины. Километр. 4 класс Свойства функции
Свойства функции Презентация по математике Деление на трехзначное число
Презентация по математике Деление на трехзначное число Векторы и их применение при доказательстве теорем
Векторы и их применение при доказательстве теорем Симметрические многочлены
Симметрические многочлены Луч и угол
Луч и угол Умножение на двузначное, трехзначное число. Урок математики для 4 класс
Умножение на двузначное, трехзначное число. Урок математики для 4 класс Превращение фигур
Превращение фигур Формулы сокращенного умножения
Формулы сокращенного умножения Информатика в задачах теплоэнергетики
Информатика в задачах теплоэнергетики Открытый конкурс Мой первый урок. Элементы теории вероятностей
Открытый конкурс Мой первый урок. Элементы теории вероятностей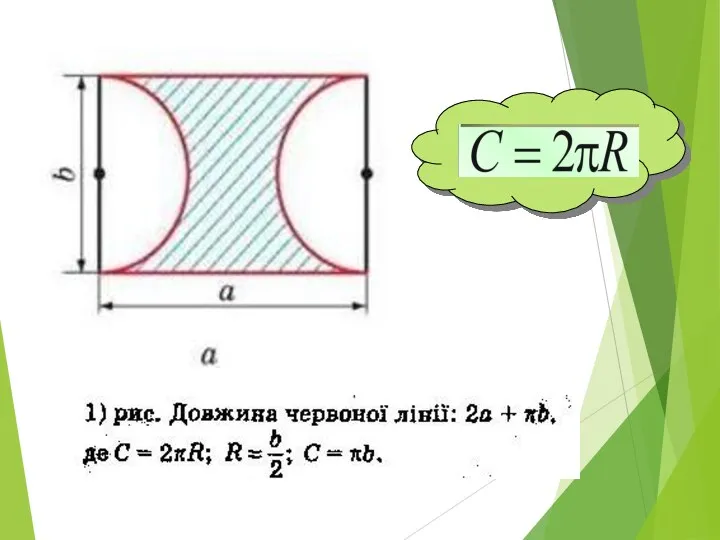 Площа круга та його частин
Площа круга та його частин Математическая логика
Математическая логика Правильные и неправильные дроби
Правильные и неправильные дроби Линейное уравнение с одной переменной. Что называется уравнением?
Линейное уравнение с одной переменной. Что называется уравнением? Воспитание гражданина на уроках математики
Воспитание гражданина на уроках математики Умножение дроби на натуральное число. Урок математики. 6 класс
Умножение дроби на натуральное число. Урок математики. 6 класс Урок 1 класс Решаем задачи.
Урок 1 класс Решаем задачи. тренажёр-раскраска
тренажёр-раскраска Математика. 1 класс. Урок 81. Сложение и вычитание величин - Презентация
Математика. 1 класс. Урок 81. Сложение и вычитание величин - Презентация применение производной к исследованию функции
применение производной к исследованию функции