7.4
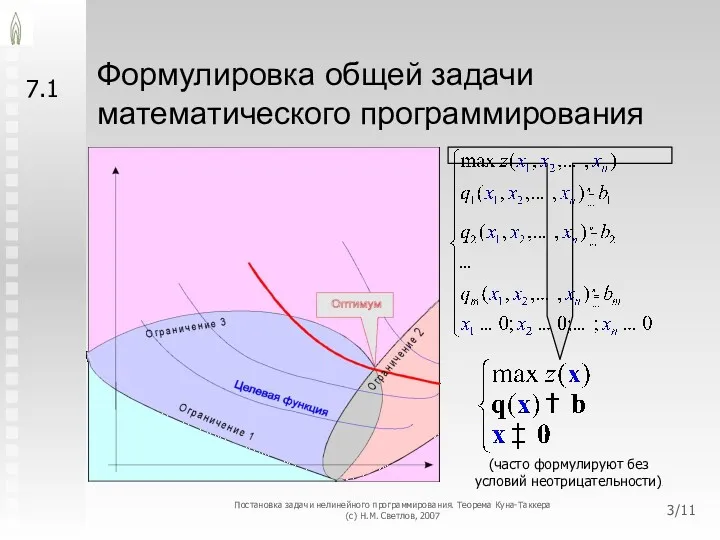
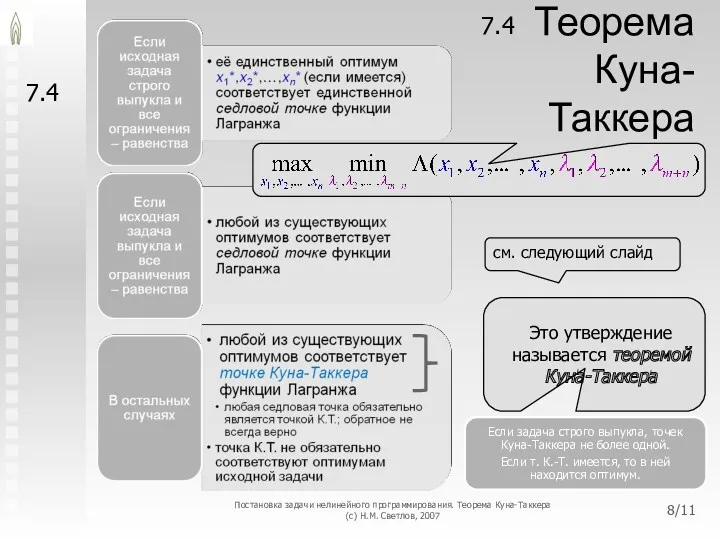
Переменные λi называются множителями Лагранжа.
Экономическая интерпретация множителей Лагранжа, соответствующих оптимальному решению,
аналогична интерпретации двойственных оценок ограничений ЗЛП
Они показывают величину изменения целевой функции в расчёте на единицу изменения свободного члена ограничения, которому соответствует множитель Лагранжа, в очень малой окрестности оптимума
Если ограничение можно рассматривать в качестве баланса ресурса и максимизируется прибыль, то множитель Лагранжа в точке оптимума равен оптимальной цене
Если найдётся рынок, где ресурс дешевле, то его покупка увеличит прибыль
Если найдётся рынок, где ресурс дороже, то для увеличения прибыли его следует продать
В отличие от случая ЗЛП, множители Лагранжа (кроме частных случаев) не обладают свойством устойчивости
Они меняют свои значения даже при сколь угодно малом изменении свободных членов ограничений
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
/11






 Презентация урока математики 4 класс по образовательной системе Школа 2100,ФГОС, с применением РНС Тема: Нахождение числа по его части
Презентация урока математики 4 класс по образовательной системе Школа 2100,ФГОС, с применением РНС Тема: Нахождение числа по его части Вивчаємо арифметичні дії множення і ділення; табличне множення і ділення
Вивчаємо арифметичні дії множення і ділення; табличне множення і ділення Сравнение десятичных дробей для урока
Сравнение десятичных дробей для урока Метод координат при решении стереометрических задач. Урок геометрии, 11 класс
Метод координат при решении стереометрических задач. Урок геометрии, 11 класс Научно-педагогическая практика. Оптимальный по парето метод обучения
Научно-педагогическая практика. Оптимальный по парето метод обучения ДУ второго порядка
ДУ второго порядка Перестановки. 9 класс
Перестановки. 9 класс Математика повсюду
Математика повсюду Взаимное расположение графиков линейной функции
Взаимное расположение графиков линейной функции Предел функции
Предел функции Тела вращения. Математический диктант
Тела вращения. Математический диктант Параллельный перенос
Параллельный перенос Схемы и графы
Схемы и графы Элективный курс по математике Практикум по решению задач
Элективный курс по математике Практикум по решению задач Наибольший общий делитель
Наибольший общий делитель Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Основные теоремы теории вероятностей
Основные теоремы теории вероятностей Перехід між кутами у правильних пірамідах
Перехід між кутами у правильних пірамідах Проблемы простых сверток. Инвариантность
Проблемы простых сверток. Инвариантность Задания по русскому языку и математике для 4 класса
Задания по русскому языку и математике для 4 класса Диаграммы
Диаграммы Как писать цифры
Как писать цифры Итоговый тест по математике за 2 класс
Итоговый тест по математике за 2 класс Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 4
Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 4 Статистика – дизайн информации
Статистика – дизайн информации Презентация Магические фигуры
Презентация Магические фигуры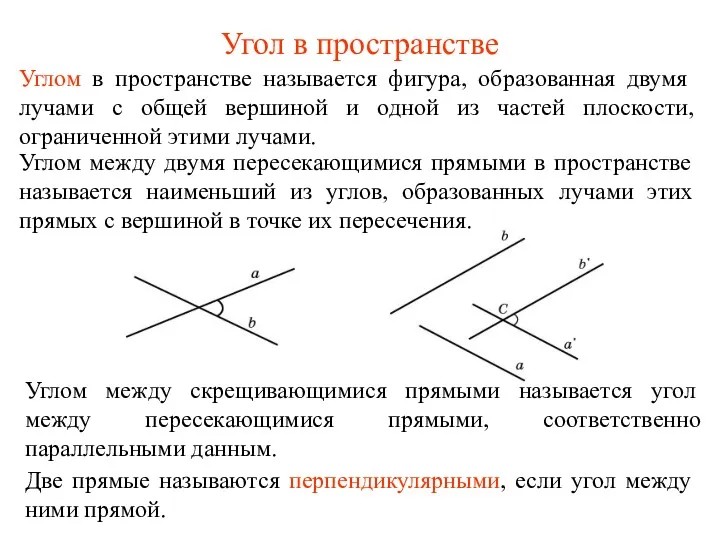 Угол в пространстве
Угол в пространстве Расстояние от точки до плоскости. Теорема о трёх перпендикулярах
Расстояние от точки до плоскости. Теорема о трёх перпендикулярах