Содержание
- 2. Для вычисления данного интеграла необходимо тем или иным способом свести его к табличному интегралу и таким
- 3. Метод подстановки (метод введения новой переменной) Пусть f(x) непрерывна на интервале (a,b) и непрерывно дифференцируема на
- 4. Метод интегрирования по частям Пусть u и v – непрерывно дифференцируемые функции от x. На основании
- 5. Интегрирование рациональных дробей с квадратичным знаменателем Рассмотрим интеграл вида , где P(x) – целочисленный многочлен; a,b,c
- 6. Тогда III. Основной прием вычисления интеграла (1) состоит в следующем: квадратный трехчлен дополняется до полного квадрата.
- 7. 4. Полагаем Производя подстановку получаем 5. Выполним тригонометрическую подстановку x=asint, dx=acostdt . Следовательно Делая обратную замену
- 8. 6. так как получаем 7. = =xlnx- 8. 9. 10. 11. 12. 13.
- 10. Скачать презентацию






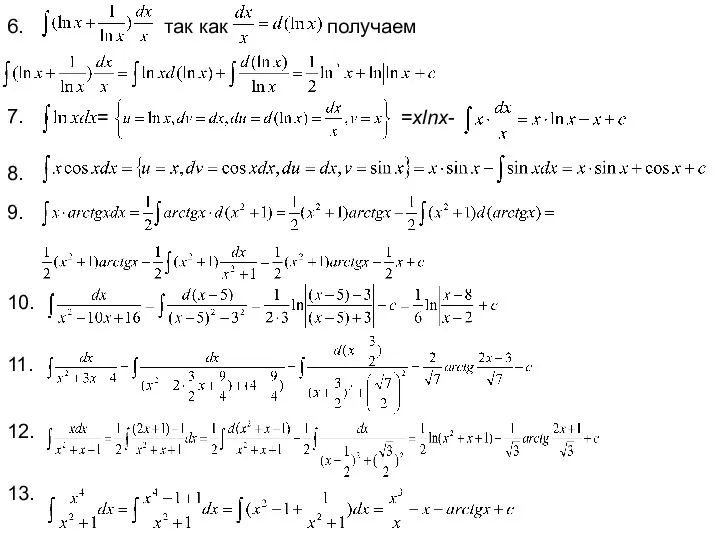
 Формулы приведения
Формулы приведения Угол. Измерение углов. Виды углов
Угол. Измерение углов. Виды углов Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ
Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ Уравнение прямой в пространстве
Уравнение прямой в пространстве Математика 2 кл. Презентация к уроку Меры длины УМК Перспектива
Математика 2 кл. Презентация к уроку Меры длины УМК Перспектива XVII век – Бунташный век в отечественной истории (интегрированный урок математики и истории в 7 классе)
XVII век – Бунташный век в отечественной истории (интегрированный урок математики и истории в 7 классе) Задачі на різницеве порівняння. Обчислення значень виразів. Урок №61
Задачі на різницеве порівняння. Обчислення значень виразів. Урок №61 Теория погрешностей
Теория погрешностей Исследование расположения корней квадратного уравнения в задачах с параметрами
Исследование расположения корней квадратного уравнения в задачах с параметрами КУС по математике для 4 класса
КУС по математике для 4 класса Алгоритмы и устройства счета. Вычисления раньше и сейчас
Алгоритмы и устройства счета. Вычисления раньше и сейчас Координатная плоскость. 7 класс
Координатная плоскость. 7 класс ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2
ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2 Корреляция. Понятие корреляционной связи
Корреляция. Понятие корреляционной связи ГИА. Открытый банк заданий по математике
ГИА. Открытый банк заданий по математике Математический диктант №3. 2 класс
Математический диктант №3. 2 класс Матрицы, определители, СЛАУ. Линейная алгебра 1
Матрицы, определители, СЛАУ. Линейная алгебра 1 Уравнение. Решение задач
Уравнение. Решение задач Умножение десятичных дробей. Деление десятичных дробей на натуральное число. 5 класс
Умножение десятичных дробей. Деление десятичных дробей на натуральное число. 5 класс Десятки с десятками, единицы с единицами
Десятки с десятками, единицы с единицами Развивающее занятие Геометрические фигуры
Развивающее занятие Геометрические фигуры Применение векторов в решении задач
Применение векторов в решении задач Численные методы решения уравнения
Численные методы решения уравнения Единицы измерения длины. Сравнение отрезков
Единицы измерения длины. Сравнение отрезков Презентация к уроку математики в 1 классе Виды треугольников Диск
Презентация к уроку математики в 1 классе Виды треугольников Диск Двойственная задача линейного программирования. Экономическая интерпретация
Двойственная задача линейного программирования. Экономическая интерпретация Устный счёт (4 класс)
Устный счёт (4 класс) Поворот и параллельный перенос
Поворот и параллельный перенос