Содержание
- 2. План лекции: Актуальность темы. Непараметрический дисперсионный анализ для зависимых выборок. Непараметрический дисперсионный анализ для независимых выборок.
- 3. Сравнение более двух зависимых выборок. Критерий Фридмана (χ2) - это непараметрический аналог дисперсионного анализа повторных измерений
- 4. Результаты наблюдения у каждого объекта упорядочиваются (по строке). Причем отдельно упорядочиваем значения у каждого объекта независимо
- 5. где N-число объектов, k-число уровней фактора (повторных измерений), Ri-сумма рангов для соответствующего уровня i. Находится χ2крит
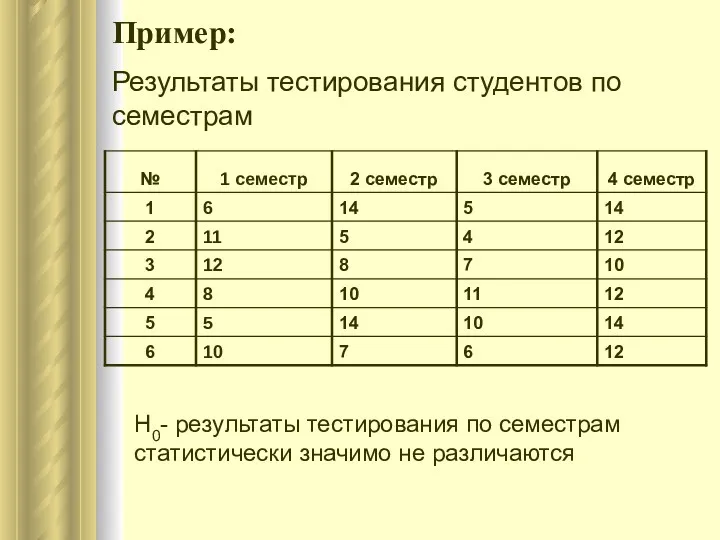
- 6. Пример: Результаты тестирования студентов по семестрам H0- результаты тестирования по семестрам статистически значимо не различаются
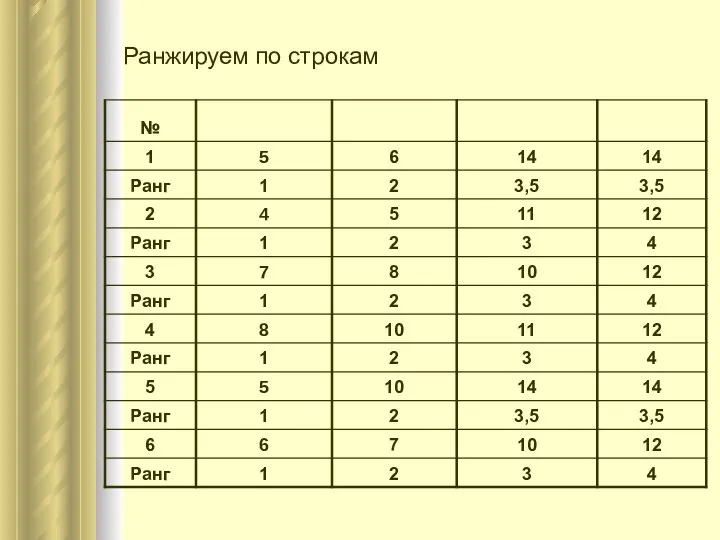
- 7. Ранжируем по строкам
- 8. Вычислим сумму рангов для каждого семестра Ri Вычислим эмпирическое значение критерия χ2 -Фридмана
- 9. Найдем χ2 крит для df=3 и α=0,05. χ2 крит=7,815 Так как 8,6 > 7,815 нулевая гипотеза
- 10. Сравнение более двух независимых выборок. Критерий Краскэла-Уоллиса. Критерий Краскэла-Уоллиса (Н) - это непараметрический аналог однофакторного дисперсионного
- 11. Значения выборок объединяются в один упорядоченный ряд. Значения объединенного ряда ранжируются. Записываются ранги отдельно для каждой
- 12. Чем сильнее различаются выборки, тем больше критерий Н и тем меньше уровень значимости. Находится критическое значение
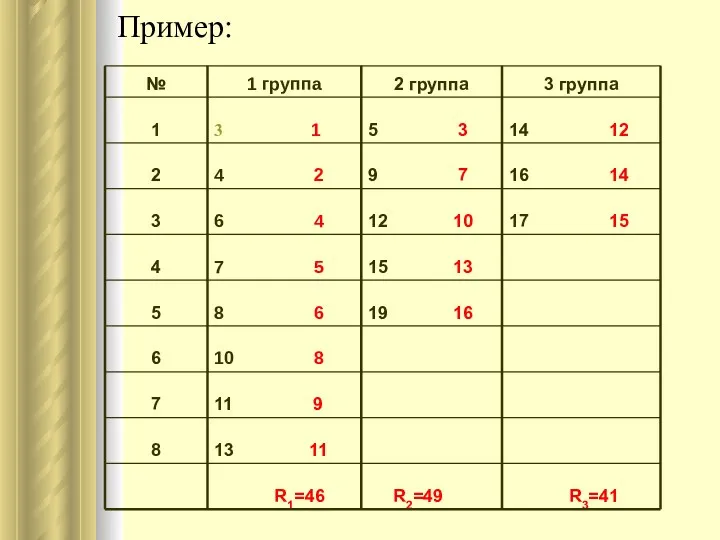
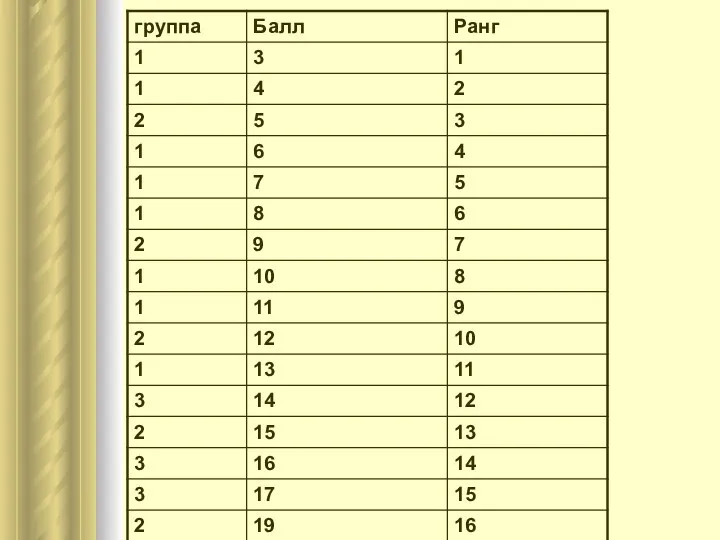
- 13. Пример:
- 15. Проверяем правильность расчетов. Общая сумма рангов должна равняться: N(N+1)/2=16⋅17/2=136 R1+R2+R3=46+49+41=136 Вычисляем Н: По таблице критических значений
- 16. Критерий Колмогорова-Смирнова используется для сравнения эмпирического распределения с теоретическим или двух эмпирических распределений друг с другом.
- 17. В качестве меры расхождения между теоретической F(x) и эмпирической Fn(x) функциями распределения непрерывной случайной величины Х
- 18. Процедура расчетов 1. Данные в выборке ранжируются по возрастанию. 2. Вычисляются кумулятивные разности: 3. Находится абсолютное
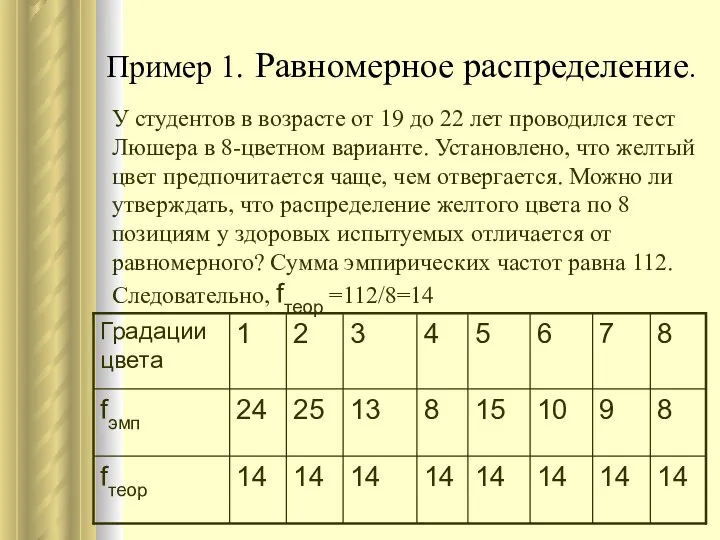
- 19. Пример 1. Равномерное распределение. У студентов в возрасте от 19 до 22 лет проводился тест Люшера
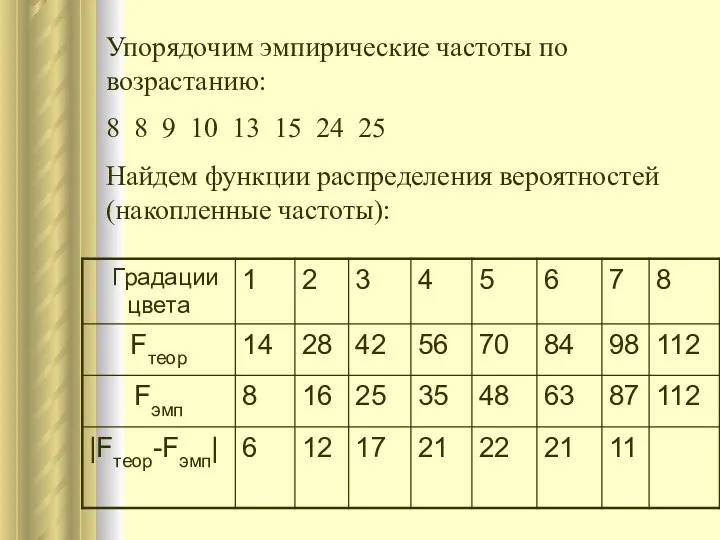
- 20. Упорядочим эмпирические частоты по возрастанию: 8 8 9 10 13 15 24 25 Найдем функции распределения
- 21. Эмпирическое значение критерия равно: Критическое значение критерия находим по таблице. Если число элементов выборки больше 100,
- 22. Для применения критерия необходимо выполнение следующих условий: Измерения должны быть проведены в шкале интервалов и отношений
- 23. Пример 2: Нормальное распределение Среднее арифметическое = -0,308; дисперсия = 1,47, стандартное отклонение = 1,28. Нулевая
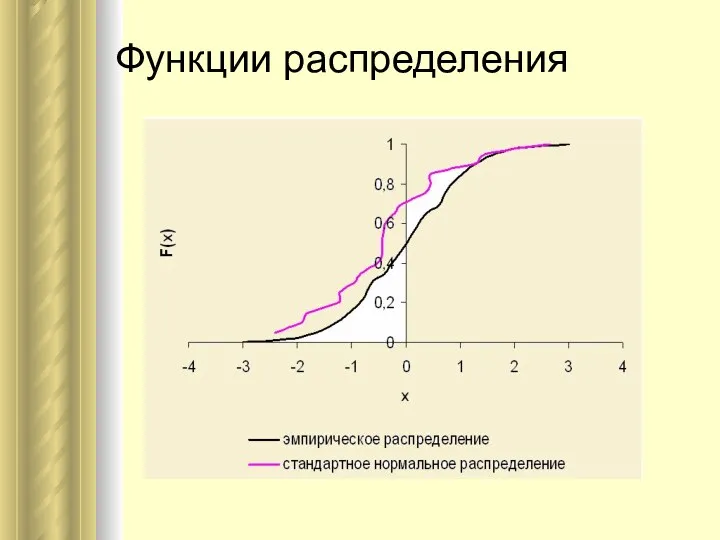
- 24. Функции распределения
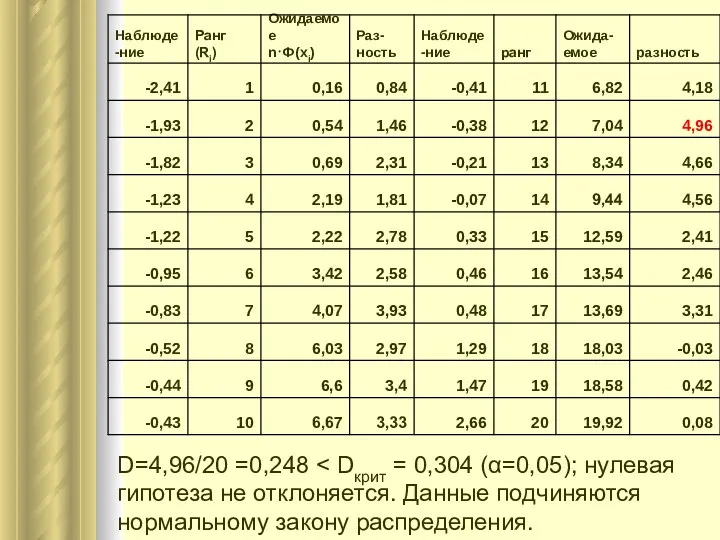
- 25. Процедура расчетов 1. Данные в выборке ранжируются по возрастанию. 2. Вычисляются кумулятивные разности: 3. Находится абсолютное
- 26. D=4,96/20 =0,248
- 27. Заключение Таким образом, нами рассмотрены основы непараметрического дисперсионного анализа, применение критерия Колмогорова-Смирнова
- 28. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Основная литература: Попов А.М. Теория вероятней и математическая статистика /А.М. Попов, В.Н. Сотников. –
- 30. Скачать презентацию



















 Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Симметрия. Виды симметрии
Симметрия. Виды симметрии Внеклассное мероприятие по сказке КОЛОБОК
Внеклассное мероприятие по сказке КОЛОБОК Окружность, хорды и диаметры, их свойства
Окружность, хорды и диаметры, их свойства Таблица умножения 3
Таблица умножения 3 Делители и кратные. 5 класс
Делители и кратные. 5 класс Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов Презентация по математике Умножение в Простоквашино
Презентация по математике Умножение в Простоквашино Комбинаторика. Правило произведения. Перестановки. Размещения
Комбинаторика. Правило произведения. Перестановки. Размещения Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Правильные многоугольники
Правильные многоугольники Задачи на смеси и сплавы
Задачи на смеси и сплавы Пределы. Числовая последовательность. Предел числовой последовательности
Пределы. Числовая последовательность. Предел числовой последовательности Аксиомы стереометрии. Следствия из аксиом. Задачи
Аксиомы стереометрии. Следствия из аксиом. Задачи Понятие производной
Понятие производной Математика. Основные разделы теста. 1 семестр
Математика. Основные разделы теста. 1 семестр Конус. Конусы вокруг нас
Конус. Конусы вокруг нас Мистика и тайны загадочного числа пи
Мистика и тайны загадочного числа пи Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Теорема Виета. Открытый урок по алгебре. 8 класс
Теорема Виета. Открытый урок по алгебре. 8 класс Сложение однозначных чисел с переходом через десяток вида + 6
Сложение однозначных чисел с переходом через десяток вида + 6 Подготовка к ОГЭ. Функции и графики: линейная функция
Подготовка к ОГЭ. Функции и графики: линейная функция Задачи и принципы квалиметрии
Задачи и принципы квалиметрии Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Подібність трикутників
Подібність трикутників Понятие функции
Понятие функции Задачи по планиметрии
Задачи по планиметрии Цифра 9
Цифра 9