Слайд 2

Определение 1
Говорят, что функция
y = f (x), x ∈ X
имеет период Т, если для любого х ∈ Х выполняется равенство
f (x – T) = f (x) = f (x + T).
Если функция с периодом Т определена в точке х, то она определена и в точках
х + Т, х – Т.
Любая функция имеет период, равный нулю
при Т = 0 получим f(x – 0) = f(x) = f(x + 0).
Слайд 3

Определение 2
Функцию, имеющую отличный от нуля период Т, называют периодической.
Если
функция y = f (x), x ∈ X имеет период Т, то любое число, кратное Т (т.е. число вида кТ, к ∈ Z), также является её периодом.
Слайд 4

Доказательство
Пусть 2Т – период функции. Тогда
f(x) = f(x + T) =
f((x + T) +T) = f(x +2T),
f(x) = f(x - T) = f((x - T) -T) = f(x - 2T).
Аналогично доказывается, что
f(x) = f(x + 3T) = f(x - 3T),
f(x) = f(x + 4T) = f(x - 4T) и т.д.
Итак, f(x - кТ) = f(x ) = f(x + кT)
Слайд 5

Наименьший период среди положительных периодов периодической функции называется основным периодом данной
функции.
Слайд 6

Особенности графика периодической функции
Если Т – основной период функции y =
f(x), то достаточно:
построить ветвь графика на одном из промежутков длины Т
выполнить параллельный перенос этой ветви вдоль оси х на ±Т, ±2Т, ±3Т и т.д.
Обычно выбирают промежуток с концами в точках
Слайд 7

Свойства периодических функций
1.Если f(x) – периодическая функция с периодом Т, то
функция g(x) = A f(kx + b), где к>0, также является периодической с периодом Т1= Т/к.
2.Пусть функция f1(x) и f2(x) определены на всей числовой оси и являются периодическими с периодами Т1 > 0 и Т2 >0. Тогда при Т1/Т2 ∈Q функция f(x) = f(x) +f2(x) – периодическая функция с периодом Т, равным наименьшему общему кратному чисел Т1 и Т2.
Слайд 8

Примеры
1. Периодическая функция y = f(x) определена для всех действительных чисел.
Её период равен 3 и f(0) =4. Найти значение выражения 2f(3) – f(-3).
Решение .
Т = 3,
f(3) =f(0+3) = 4,
f(-3) = f(0–3) =4, f(0) = 4.
Подставив полученные значения в выражение
2f(3) – f(-3), получим 8 - 4 =4.
Ответ: 4.
Слайд 9

Примеры
2. Периодическая функция y = f(x) определена для всех действительных чисел.
Её период равен 5, а f(-1) = 1.Найти f(-12),если 2f(3) – 5f(9) = 9.
Решение
Т = 5
F(-1) = 1
f(9) = f(-1 +2T) = 1⇨ 5f(9) = 5
2f(3) = 9 + 5f(9) = 14 ⇨f(3)= 7
F(-12) = f(3 – 3T) = f(3) = 7
Ответ:7.








 Сказочная страна функций. Электронный урок
Сказочная страна функций. Электронный урок Парная линейная регрессионная модель
Парная линейная регрессионная модель Урок математики в 1 класс по теме Сложение с нулем дидактическая система Л.В.Занкова
Урок математики в 1 класс по теме Сложение с нулем дидактическая система Л.В.Занкова Положительные и отрицательные числа
Положительные и отрицательные числа Подобные треугольники. Геометерия. 8 класс
Подобные треугольники. Геометерия. 8 класс Скалярное произведение векторов. 9 класс
Скалярное произведение векторов. 9 класс Нумерация чисел от 11 до 20
Нумерация чисел от 11 до 20 Урок 22 Сложение двузначного числа и однозначного с переходом через разряд.
Урок 22 Сложение двузначного числа и однозначного с переходом через разряд. Рух: швидкість, час, відстань. Математика 4 клас
Рух: швидкість, час, відстань. Математика 4 клас Параллелепипед. Типы параллелепипеда
Параллелепипед. Типы параллелепипеда Метод координат
Метод координат интерактивный тренажёр Сложение и вычитание в пределах 20
интерактивный тренажёр Сложение и вычитание в пределах 20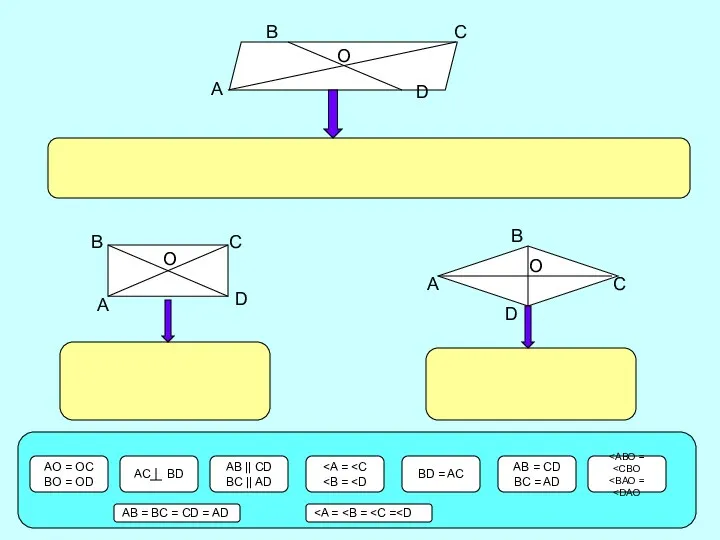 Прямоугольник, ромб, квадрат. Решение задач по готовому чертежу
Прямоугольник, ромб, квадрат. Решение задач по готовому чертежу Подготовка к ОГЭ на уроках математики в 9 классе
Подготовка к ОГЭ на уроках математики в 9 классе Метод интервалов решения дробно-рациональных неравенств
Метод интервалов решения дробно-рациональных неравенств Число ноль
Число ноль Формулы сокращенного умножения. Урок – пресс-конференция
Формулы сокращенного умножения. Урок – пресс-конференция Математический аукцион. Решение задач
Математический аукцион. Решение задач Площади. Равновеликие фигуры
Площади. Равновеликие фигуры Умножение 7 и на 7
Умножение 7 и на 7 Корреляционный анализ
Корреляционный анализ Подготовка к ЕГЭ. Задание 8
Подготовка к ЕГЭ. Задание 8 Подобные треугольников. Признаки подобия треугольников. 8 класс
Подобные треугольников. Признаки подобия треугольников. 8 класс выбор метода_преподаватели
выбор метода_преподаватели Определение расстояния до недоступной точки. Определение высоты недоступного предмета
Определение расстояния до недоступной точки. Определение высоты недоступного предмета Симметрия - математический закон красоты
Симметрия - математический закон красоты Числа 1, 2, 3. Знаки +, -, =
Числа 1, 2, 3. Знаки +, -, = Формула стоимости
Формула стоимости