Содержание
- 2. Основные вопросы: Определение первообразной. Основное свойство первообразной. Понятие неопределенного интеграла. Основные формулы интегрирования. Непосредственное интегрирование (метод
- 3. Определение первообразной. Основное свойство первообразной. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном
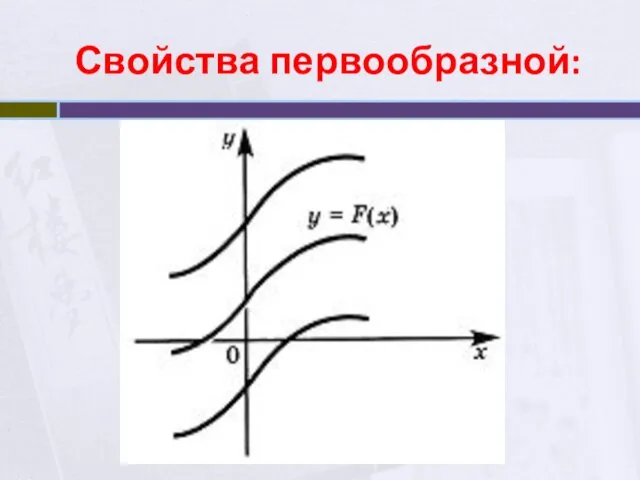
- 4. Свойства первообразной: Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x)
- 5. Свойства первообразной:
- 6. Свойства первообразной: 2. Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то
- 7. Свойства первообразной: 3. Для любой первообразной F(x) выполняется равенство dF(x) = f(x) dx. Из этих свойств
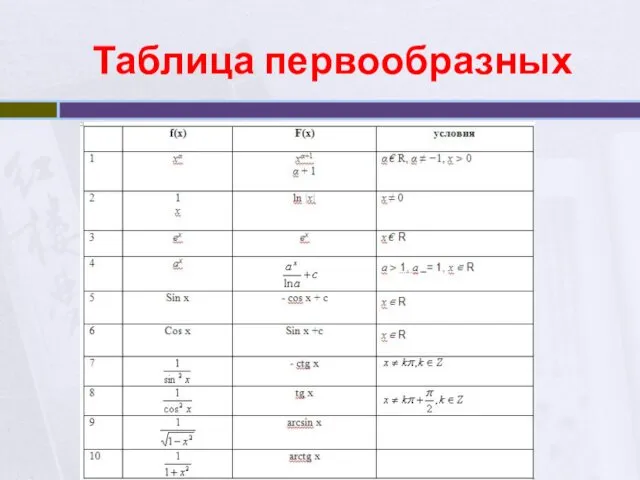
- 8. Таблица первообразных
- 9. Понятие неопределенного интеграла. Основные формулы интегрирования Множество первообразных функции f(x) называется неопределённым интегралом от этой функции
- 10. поскольку функция - первообразная для функции х4. Процесс нахождения неопределенного интеграла функции называется интегрированием этой функции.
- 11. Свойства неопределенного интеграла: 1. Производная неопределенного интеграла равна подынтегральной функции: Это свойство считается очень важным, его
- 12. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению: Свойства неопределенного интеграла:
- 13. 3. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная: Свойства неопределенного интеграла:
- 14. 4.Постоянный множитель можно выносить за знак неопределенного интеграла: Свойства неопределенного интеграла:
- 15. 5.Неопределенный интеграл от суммы 2-х функций равен сумме неопределенных интегралов от этих функций: Свойства неопределенного интеграла:
- 16. Таблица неопределенных интегралов:
- 17. Таблица неопределенных интегралов:
- 18. Непосредственное интегрирование (метод разложения). Непосредственным интегрированием называется метод нахождения интегралов, основанный на использовании таблицы и основных
- 21. Отметим несколько полезных правил для вычисления интегралов.
- 23. Найти Решение: введем подстановку u = 5x + 3 дифференциал этого выражения: d (5x + 3)
- 24. Заменив u его выражением через x, имеем: Проверка: Интеграл найден правильно.
- 25. Решение: Заменяя переменную в данном интеграле, имеем: Подставляя вместо t его выражение через x, найдем:
- 27. Интегрирование некоторых тригонометрических функций. Интегралы от произведений синусов и косинусов с разными аргументами, линейно зависящими от
- 28. Вычислим интеграл Преобразуем произведение в сумму: тогда
- 29. Упражнения :
- 31. Скачать презентацию


























 Обобщающий урок по теме параллелограмм 8 класс
Обобщающий урок по теме параллелограмм 8 класс Тетраэдр. Сечение тетраэдра
Тетраэдр. Сечение тетраэдра Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса Презентация по математике по теме Логарифм для 10-11 класса
Презентация по математике по теме Логарифм для 10-11 класса Обчислення на основі нумерації. Складання задач різних типів за малюнками та частиною умови. Урок №111
Обчислення на основі нумерації. Складання задач різних типів за малюнками та частиною умови. Урок №111 Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел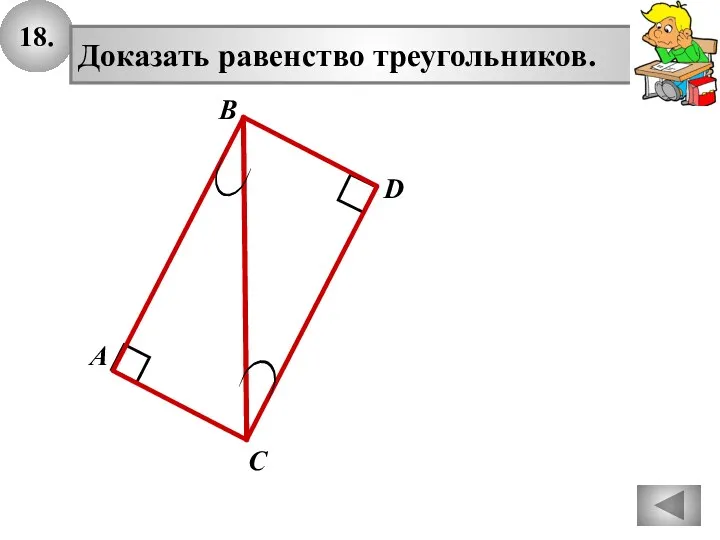 Прямоугольные треугольники
Прямоугольные треугольники Что такое умножение
Что такое умножение Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе
Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе Выражения, равенства, неравенства, уравнения .
Выражения, равенства, неравенства, уравнения . Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1)
Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1) Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций нескольких переменных Сумма и разность дробей
Сумма и разность дробей Математические модели
Математические модели Длина окружности и площадь круга
Длина окружности и площадь круга Логарифмическая функция, ее график и свойства
Логарифмическая функция, ее график и свойства Разложение на множители суммы и разности кубов
Разложение на множители суммы и разности кубов Метрические задачи
Метрические задачи Основные сведения теории вероятностей. Надежность технических систем и техногенный риск
Основные сведения теории вероятностей. Надежность технических систем и техногенный риск Сложение однозначных чисел с переходом через десяток вида + 8, +9
Сложение однозначных чисел с переходом через десяток вида + 8, +9 Решение системы способом подстановки. 7 класс
Решение системы способом подстановки. 7 класс Решение систем линейных уравнений. 7 класс
Решение систем линейных уравнений. 7 класс Презентация Метр 2 класс
Презентация Метр 2 класс Графический метод решения уравн
Графический метод решения уравн Вычислительная математика. Лекция 5. Системы линейных алгебраических уравнений
Вычислительная математика. Лекция 5. Системы линейных алгебраических уравнений Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс Презентация Устный счёт 2 класс 1 четверть № 3
Презентация Устный счёт 2 класс 1 четверть № 3