Содержание
- 2. Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости, которую в XIX в. ввёл французский
- 3. А, вот, прямоугольную систему координат в пространстве ввёл швейцарский, немецкий, российский математик Леонард Эйлер в XVIIIв.
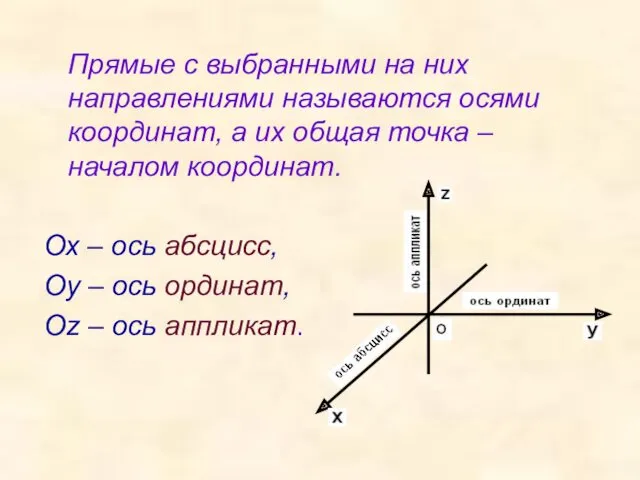
- 4. Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.
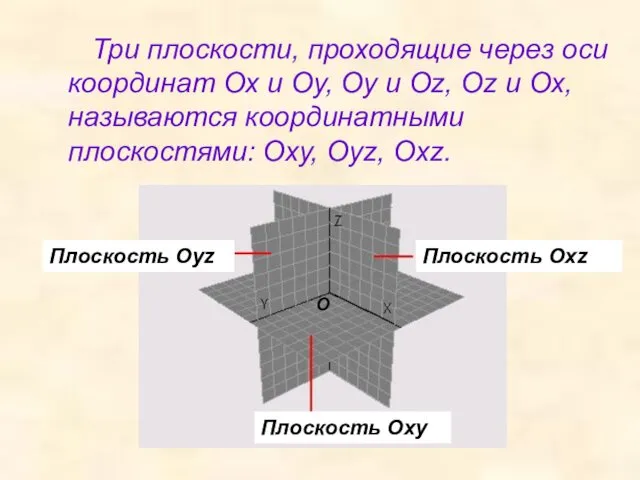
- 5. Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются
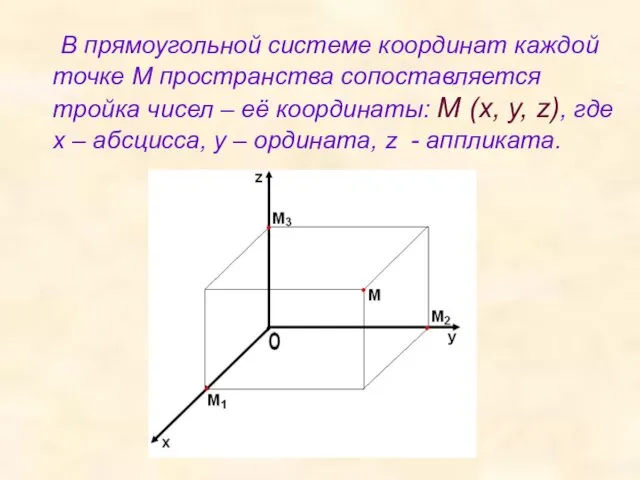
- 6. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты: М (х,
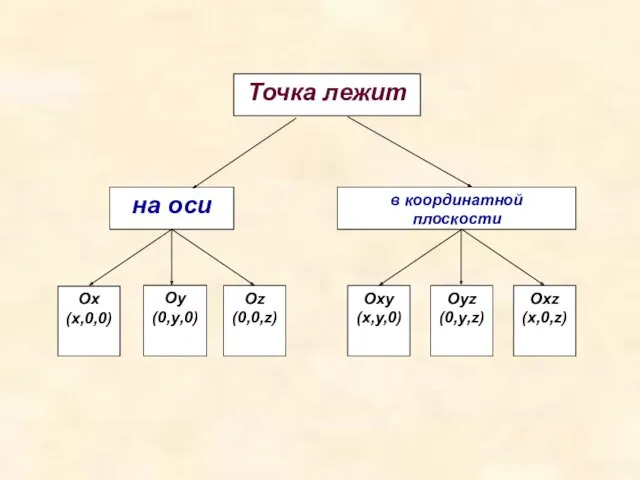
- 7. Нахождение точки на координатной плоскости. Если, например, точка M лежит на координатной плоскости или на оси
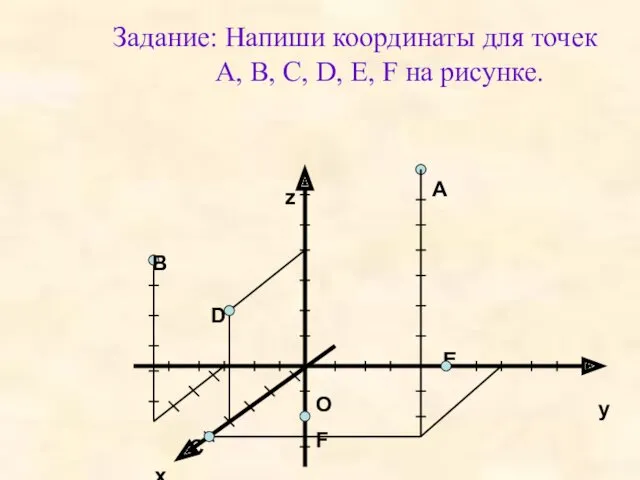
- 8. Задание: Напиши координаты для точек A, B, C, D, E, F на рисунке. B C O
- 9. Ответы. A(5; 4; 10), B(4; -3; 6), C(5; 0; 0), D(4; 0; 4), E(0; 5; 0),
- 10. Оу (0,у,0)
- 11. Если М ОХУ, то z=0 Если М OXZ, то у=0 Если М OУZ, то X=0 Если
- 12. Координаты вектора в пространстве
- 13. Единичный вектор – вектор, длина которого равна 1. i – единичный вектор оси абсцисс, j –
- 14. Любой вектор ā можно разложить по координатным векторам, т.е. представить в виде: Нулевой вектор можно представить
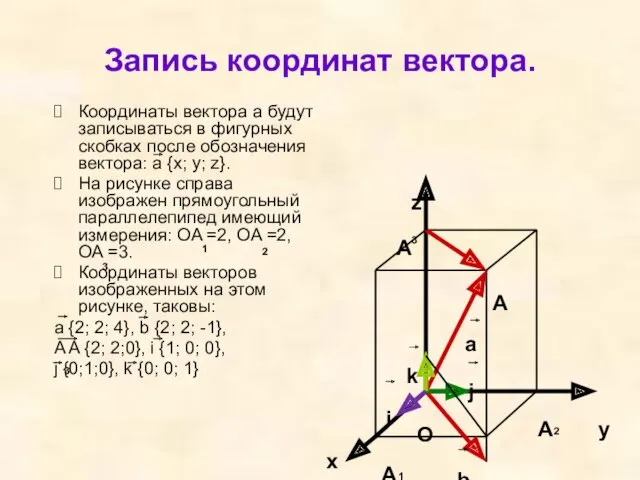
- 15. Запись координат вектора. Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x;
- 16. Сложение векторов Правило треугольника. Правило параллелограмма. Правило многоугольника. Правило параллелепипеда.
- 17. Правило треугольника А B C
- 18. Правило треугольника А B C Для любых трех точек А, В и С справедливо равенство:
- 19. Правило параллелограмма А B C
- 20. Правило многоугольника Сумма векторов равна вектору, проведенному из начала первого в конец последнего(при последовательном откладывании). B
- 21. Правило параллелепипеда B А C D A1 B1 C1 D1 Вектор, лежащий на диагонали параллелепипеда, равен
- 22. Угол между векторами
- 23. Угол между двумя ненулевыми векторами называется угол между направлениями этих векторов. ) a b a b
- 24. О А В α Если а || b и а и b сонаправлены, то α =
- 26. Скалярное произведение векторов
- 27. Скалярное произведение Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 28. a · b = | a | · | b | · cos(a ^ b) 2)
- 30. Скачать презентацию



















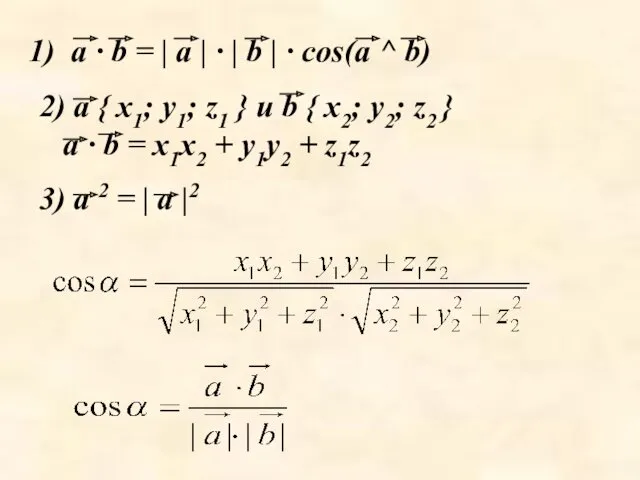
 Функция y=k/x, её график и свойства. 8 класс. Урок 1
Функция y=k/x, её график и свойства. 8 класс. Урок 1 Введение в статистику
Введение в статистику Презентация Час. Минута
Презентация Час. Минута Игра Математический лабиринт
Игра Математический лабиринт Урок 30. Линейная функция у = кх
Урок 30. Линейная функция у = кх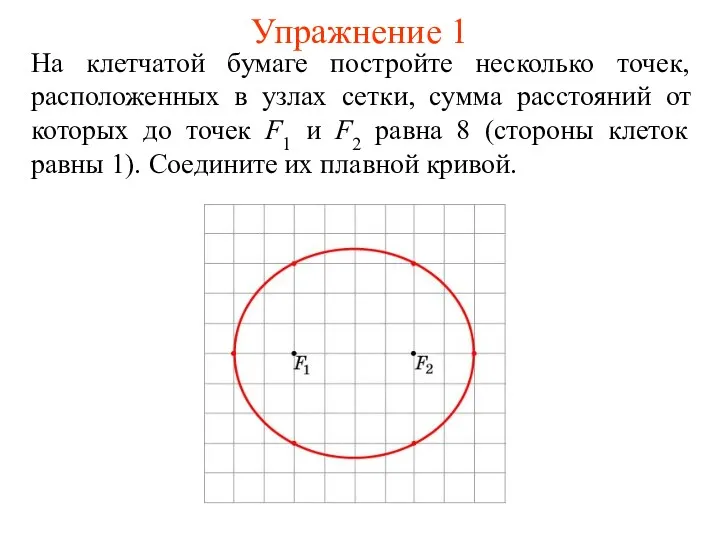 Эллипс
Эллипс Итоговое повторение по геометрии, 7 класс
Итоговое повторение по геометрии, 7 класс Измерение углов
Измерение углов презентация на тему Организм человека
презентация на тему Организм человека Теория надежности. Вероятность безотказной работы и вероятность отказа. Распределение Вейбулла
Теория надежности. Вероятность безотказной работы и вероятность отказа. Распределение Вейбулла Математические олимпийские игры
Математические олимпийские игры Урок математики
Урок математики 1 класс презентация к уроку Уравнение
1 класс презентация к уроку Уравнение Итоговый тест по математике
Итоговый тест по математике Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве
Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве Функции y=sinx, y=cosx. Свойства. Преобразование графиков
Функции y=sinx, y=cosx. Свойства. Преобразование графиков Подготовка к ГИА по математике. Задания 16
Подготовка к ГИА по математике. Задания 16 Презентация к уроку русского языка в 4 классе Неопределённая форма глагола
Презентация к уроку русского языка в 4 классе Неопределённая форма глагола ГИА - 2015 Модуль Алгебра
ГИА - 2015 Модуль Алгебра Замечательные кривые в математике
Замечательные кривые в математике Усвоение грамматических форм языка на занятиях по математике
Усвоение грамматических форм языка на занятиях по математике Скорость. Время. Расстояние.
Скорость. Время. Расстояние. Перпендикулярность прямой и плоскости. Задания для устного счета. Упражнение 7
Перпендикулярность прямой и плоскости. Задания для устного счета. Упражнение 7 Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи Скалярное произведение векторов
Скалярное произведение векторов Дискретна математика. Декартів добуток множин
Дискретна математика. Декартів добуток множин Число-9
Число-9 Декартова система координат в пространстве
Декартова система координат в пространстве