Содержание
- 2. Шкалы измерений Номинальная шкала (шкала наименований). Эта шкала используется только для того, чтобы отнести объект или
- 3. Математическое ожидание Если совокупность случайных величин задана в виде набора дискретных значений, то математическое ожидание случайной
- 4. Дисперсия Числовой характеристикой, показывающей степень разброса значений случайной величины относительно математического ожидания, называется дисперсия
- 5. Среднеквадратическое отклонение Поскольку дисперсия имеет размерность квадрата случайной величины, то для характеристики меры рассеяния значений случайной
- 6. Выборочное среднее, дисперсия и среднеквадратическое отклонение Выборочное среднее, представляющее собой оценку математического ожидания генеральной совокупности: Выборочная
- 7. Понятие закона распределения Полное описание случайной величины дается законом распределения, который устанавливает зависимость между возможными значениями
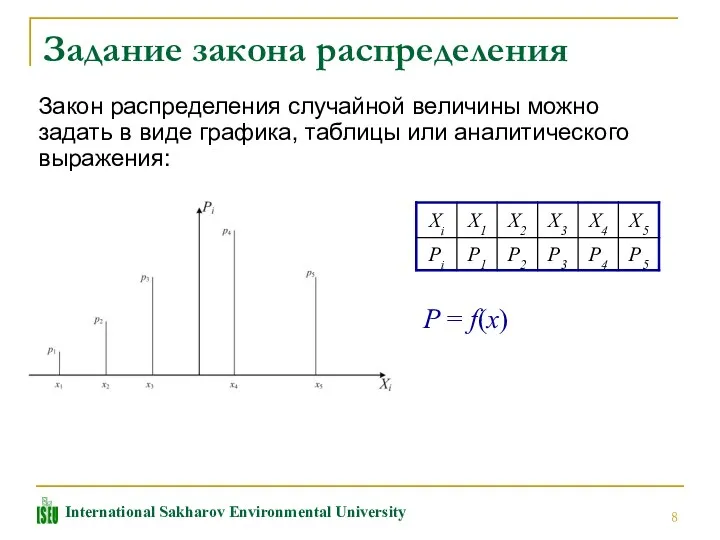
- 8. Задание закона распределения Закон распределения случайной величины можно задать в виде графика, таблицы или аналитического выражения:
- 9. Нормальное распределение оно симметрично относительно m имеет максимум равный монотонно убывает при возрастании Характеристики распределения Гаусса:
- 10. Нормальное распределение Функция распределения, показывающая вероятность случайной величине принять значение меньшее x, определяется выражением
- 11. Нормальное распределение
- 12. Нормальное распределение
- 13. Нормальное распределение
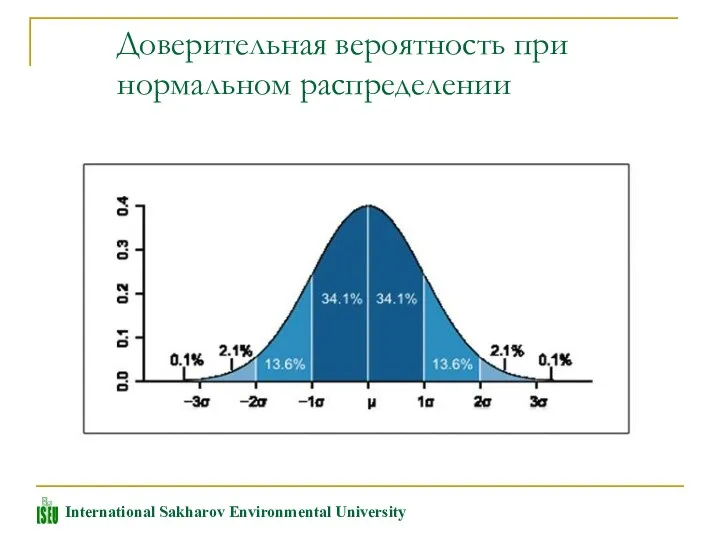
- 14. Доверительная вероятность при нормальном распределении Если случайная величина распределена по нормальному закону с математическим ожиданием μ
- 15. Доверительная вероятность при нормальном распределении
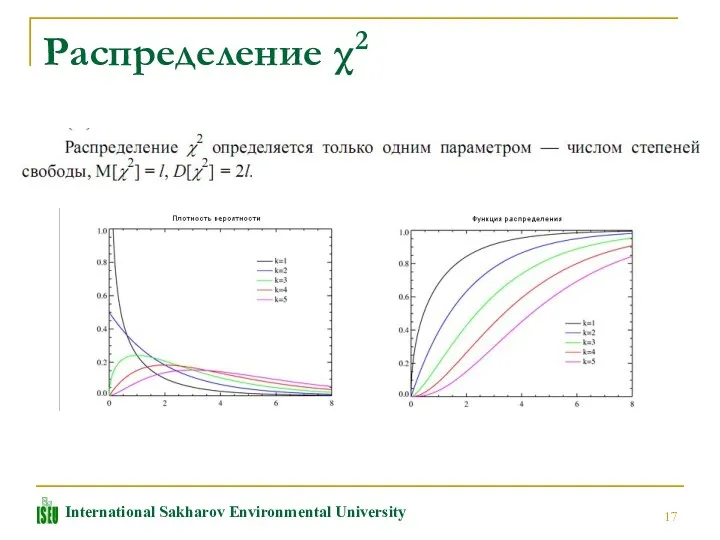
- 16. Распределение χ2
- 17. Распределение χ2
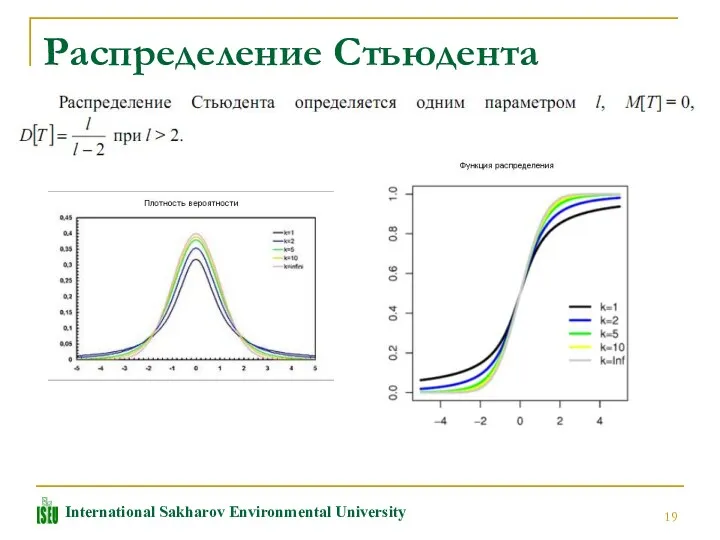
- 18. Распределение Стьюдента
- 19. Распределение Стьюдента
- 20. Проверка статистических гипотез Для того чтобы иметь основания принять или отвергнуть рассматриваемую гипотезу необходимо выработать некоторый
- 21. Здесь: m ─ число значений, принятых случайной величиной, n – общее число наблюдений, pk ─ вероятность
- 22. Непараметрический критерий Вилкоксона для проверки однородности двух независимых выборок Большинство непараметрических критериев основано на использовании рангов
- 23. Ранги и ранжирование Трудности в назначении рангов возникают, если среди элементов выборки встречаются совпадающие. В этом
- 24. Непараметрический критерий Вилкоксона В критерии Вилкоксона в качестве в качестве статистики используется случайная величина Здесь Rj
- 25. Непараметрический критерий Вилкоксона Для проверки с уровнем значимости α гипотезы H0 об однородности выборок при альтернативной
- 26. Критерий Вилкоксона для проверки однородности двух зависимых выборок Порядок применения критерия следующий: Вычисляются абсолютные разности наблюдений
- 27. Критерий Вилкоксона для проверки однородности двух зависимых выборок Вычисляется сумма значений рангов, которая образует статистику T.
- 28. Критерий Вилкоксона для проверки однородности двух зависимых выборок Если вычисленное значение статистики T то гипотеза об
- 29. Однофакторный дисперсионный анализ. Проверка гипотезы о влиянии фактора на исследуемую величину Рассмотрим простейший случай дисперсионного анализа,
- 30. Проверка гипотезы о влиянии фактора на исследуемую величину Оценка генерального среднего Несмещенная оценка дисперсии генеральной совокупности
- 31. Проверка гипотезы о влиянии фактора на исследуемую величину При справедливости нулевой гипотезы любая из выборочных дисперсий
- 32. Проверка гипотезы о влиянии фактора на исследуемую величину Оценим теперь дисперсию совокупности по выборочным средним. Поскольку
- 33. Проверка гипотезы о влиянии фактора на исследуемую величину В результате задача проверки гипотезы H0 сводится к
- 34. Проверка гипотезы о влиянии фактора на исследуемую величину Влияние фактора A на исследуемый признак считается значимым
- 35. Проверка гипотезы о влиянии фактора на исследуемую величину Результаты дисперсионного анализа в общем случае обычно представляют
- 36. Двухфакторный дисперсионный анализ. Виды взаимосвязи между двумя факторами Пусть на исследуемую величину могут оказывать влияние два
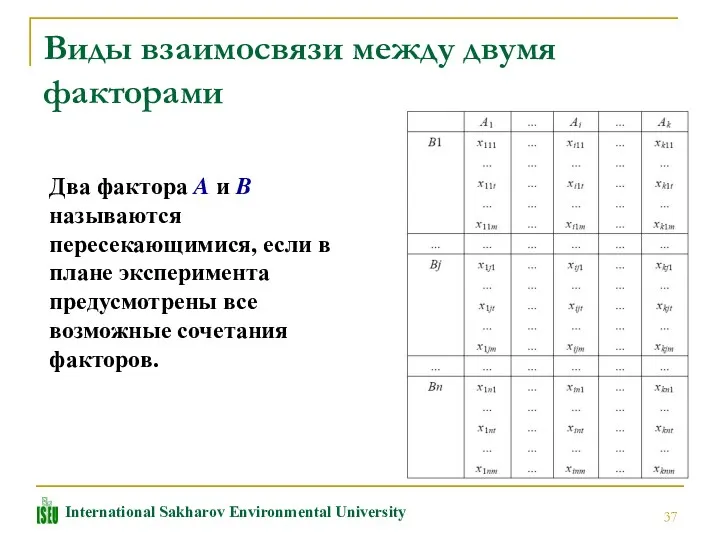
- 37. Виды взаимосвязи между двумя факторами Два фактора A и B называются пересекающимися, если в плане эксперимента
- 38. Виды взаимосвязи между двумя факторами Фактор B группируется фактором A, если каждый уровень фактора B сочетается
- 39. Двухфакторный дисперсионный анализ с пересечением уровней Рассматривая совокупность данных как одну выборку из генеральной совокупности, получим
- 40. Двухфакторный дисперсионный анализ с пересечением уровней Входящую в оценку дисперсии генеральной совокупности сумму квадратов можно представить
- 41. Двухфакторный дисперсионный анализ с пересечением уровней характеризует эффект взаимодействия факторов остаточная сумма квадратов
- 42. Двухфакторный дисперсионный анализ с пересечением уровней С учетом числа степеней свободы каждой суммы квадратов, получим следующие
- 43. Двухфакторный дисперсионный анализ с пересечением уровней Гипотеза H0 : α1 = α2 = ... = αk
- 44. Двухфакторный дисперсионный анализ с пересечением уровней Гипотеза об отсутствии взаимодействия между факторами (гипотеза об аддитивности) проверяется
- 45. Двухфакторный дисперсионный анализ с пересечением уровней Результаты дисперсионного анализа представляют следующей таблицей
- 46. Фактор B группируется фактором A, если каждый уровень фактора B сочетается не более, чем с одним
- 47. Двухфакторный дисперсионный анализ с группировкой уровней Результаты дисперсионного анализа оформляются в виде следующей таблицы
- 48. Двухфакторный дисперсионный анализ с группировкой уровней Статистики для проверки гипотез имеют вид: для гипотезы H0: σb(a)
- 49. Задачи корреляционного анализа В математическом анализе зависимость между величинами x и y выражается функцией y =
- 50. Задачи корреляционного анализа Таким образом задача корреляционного анализа исследование наличия взаимосвязей между отдельными группами переменных и
- 51. Измерители парной статистической связи. Корреляционное отношение Аналогично определяется квадрат корреляционного отношения ρ2xy переменной X по Y.
- 52. Измерители парной статистической связи. Корреляционное отношение Положительный корень из ρ2yx носит название корреляционного отношения, которое является
- 53. Измерители парной статистической связи В общем случае показатели ρ2xy и r2 связаны неравенствами При этом возможны
- 54. Измерители парной статистической связи Таким образом, в качестве показателя статистической связи между двумя случайными количественными переменными
- 55. Регрессионный анализ
- 56. Основные понятия регрессионного анализа Для математического описания статистических связей между изучаемыми переменными величинами следует решить следующие
- 57. Простая линейная регрессия Простейшей моделью регрессии является простая (одномерная, однофакторная, парная) линейная модель, имеющая следующий вид:
- 58. Простая линейная регрессия Для нахождения оценок параметров a и b линейной регрессии, определяющих наиболее удовлетворяющую экспериментальным
- 59. Простая линейная регрессия Для минимизации D приравняем к нулю частные производные по a и b: В
- 60. Простая линейная регрессия Решение этих двух уравнений дает:
- 61. Выражения для оценок параметров a и b можно представить также в виде: Простая линейная регрессия
- 62. Простая линейная регрессия Тогда эмпирическое уравнение регрессионной прямой Y на X можно записать в виде:
- 63. Несмещенная оценка дисперсии σ2 отклонений значений yi oт подобранной прямой линии регрессии дается выражением (остаточная дисперсия)
- 64. Проверка значимости линии регрессии Найденная оценка b ≠ 0 может быть реализацией случайной величины, математическое ожидание
- 65. Проверка значимости линии регрессии Вычисления по проверки значимости регрессии проводят в следующей таблице дисперсионного анализа
- 66. Проверка адекватности линейной модели регрессии Под адекватностью построенной регрессионной модели понимается то, что никакая другая модель
- 67. Коэффициент детерминации Иногда для характеристики качества линии регрессии используют выборочный коэффициент детерминации R2, показывающий, какую часть
- 68. Максимальное значение R2 = 1 может быть достигнуто только в случае, когда наблюдения проводились при различных
- 69. Применительно к простой линейной регрессии Отметим, что коэффициент R2 имеет смысл рассматривать только при наличии в
- 70. Сравнение двух линий регрессии Часто требуется сравнить линии регрессии, рассчитанные по двум выборкам. Это можно сделать
- 71. Сравнение двух линий регрессии Если нужно проверить, значимо ли различие в наклоне двух прямых регрессии, критерий
- 72. Сравнение двух линий регрессии Если обе регрессии оценены по одинаковому числу наблюдений, то стандартная ошибка разности
- 73. Сравнение двух линий регрессии Аналогично сравниваются и коэффициенты сдвига a1 и а2. В этом случае где
- 74. Сравнение двух линий регрессии Таким образом алгоритм сравнения двух линии регрессии следующий: Построить прямую регрессии для
- 75. Множественная линейная регрессия Модель множественной линейной регрессии имеет следующий вид: Предположения относительно множественной линейной регрессии аналогичны
- 76. Множественная линейная регрессия Для получения оценок параметров b0, b1, ...,bk методом наименьших квадратов нужно минимизировать по
- 77. Множественная линейная регрессия Приравняв нулю частные производные после упрощений получается следующая система нормальных уравнений для нахождения
- 78. Множественная линейная регрессия Пусть b – вектор-столбец размера (k+ 1), состоящий из коэффициентов b0 , b1,
- 79. Множественная линейная регрессия Тогда уравнение модели регрессии можно записать в виде: Выражение для D можно представить
- 81. Скачать презентацию









































































 Тема. Деление на круглое число.
Тема. Деление на круглое число. Задачи на уменьшение числа в несколько раз. 3 класс
Задачи на уменьшение числа в несколько раз. 3 класс Презентация: Шар. Порядковый счет до 3
Презентация: Шар. Порядковый счет до 3 Транспортная задача
Транспортная задача Геометрия. Задания ОГЭ
Геометрия. Задания ОГЭ Метр 2 класс
Метр 2 класс Презентация по теме Решение задач на движение 3 класс
Презентация по теме Решение задач на движение 3 класс Вартість. Гривня і копійка. Дії з іменованими числами. Урок №101
Вартість. Гривня і копійка. Дії з іменованими числами. Урок №101 Решение экономических задач в новой версии ЕГЭ
Решение экономических задач в новой версии ЕГЭ Степенева функція
Степенева функція Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ
Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем
Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем Упрощение логических выражений
Упрощение логических выражений класс геометрия повторение. Четырёх
класс геометрия повторение. Четырёх Способы решений систем линейных уравнений
Способы решений систем линейных уравнений Деление на десятичную дробь
Деление на десятичную дробь Числові множини. Ірраціональні та дійсні числа
Числові множини. Ірраціональні та дійсні числа Математическая игра Брейн-ринг. 6 класс
Математическая игра Брейн-ринг. 6 класс Неравенства с двумя переменными. 9 класс
Неравенства с двумя переменными. 9 класс Игра для учащихся Математический активизатор
Игра для учащихся Математический активизатор 20231019_lektsiya1.vektory_i_deystviya_nad_nimi_1
20231019_lektsiya1.vektory_i_deystviya_nad_nimi_1 Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Неопределенный интеграл. (Лекция 1)
Неопределенный интеграл. (Лекция 1) Правильная треугольная пирамида
Правильная треугольная пирамида презентация проекта Развитие у детей чувства времени
презентация проекта Развитие у детей чувства времени Множественная линейная регрессия
Множественная линейная регрессия Связь между слагаемым и суммой
Связь между слагаемым и суммой Рациональные уравнения. ЕГЭ. Задание 5
Рациональные уравнения. ЕГЭ. Задание 5