Содержание
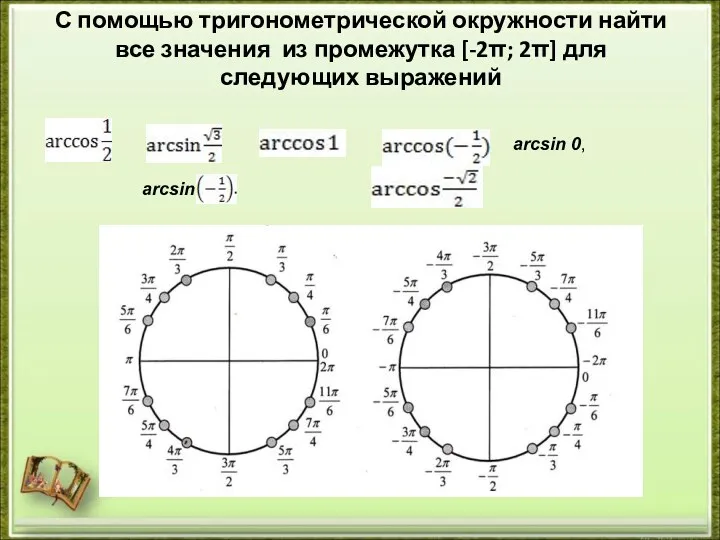
- 2. С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π] для следующих выражений arcsin 0,
- 3. Верно ли равенство
- 4. Имеет ли смысл выражение:
- 5. «Верно - неверно». 1) sin2x+cos2x=1 – основное тригонометрическое тождество? 2) [-1;1] – область значения функций sinx
- 6. «Верно - неверно» ОТВЕТЫ нет да да нет нет да нет да да нет
- 7. Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из
- 8. Решение простейших тригонометрических уравнений.
- 9. * 2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности; 4) знать
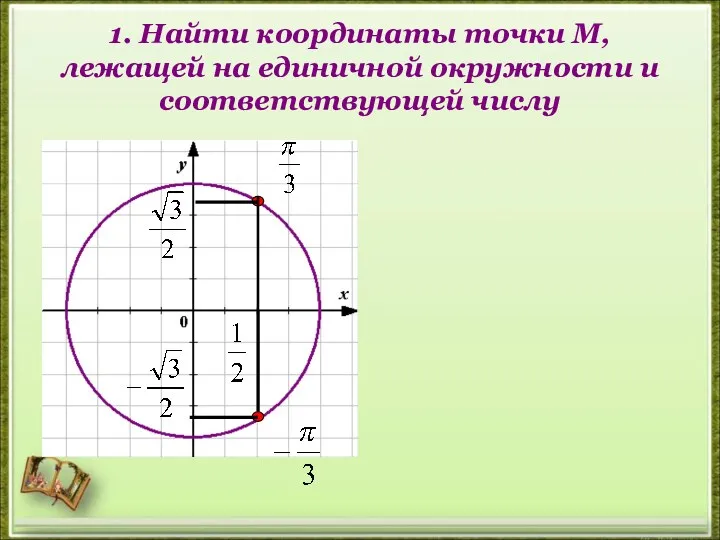
- 10. 1. Найти координаты точки М, лежащей на единичной окружности и соответствующей числу
- 11. 2. Дана точка М с абсциссой ½. Найдите ординату этой точки; укажите три угла поворота, в
- 12. 3. Дана точка М с абсциссой -½. Найдите ординату этой точки; укажите три угла поворота, в
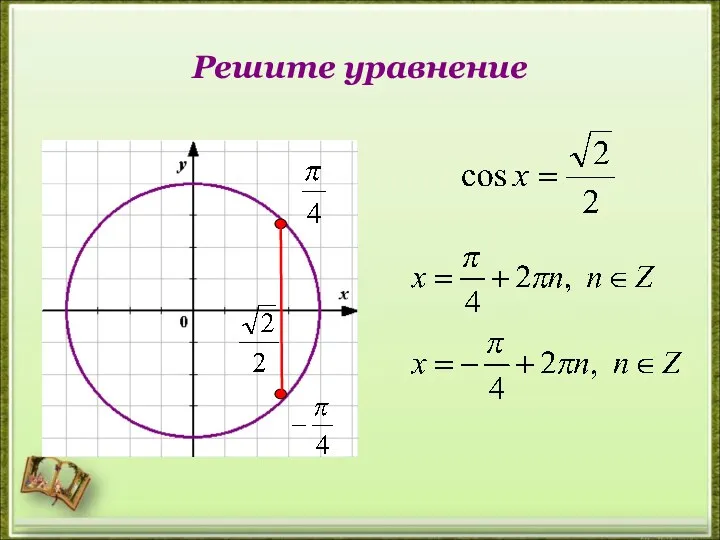
- 13. Решите уравнение
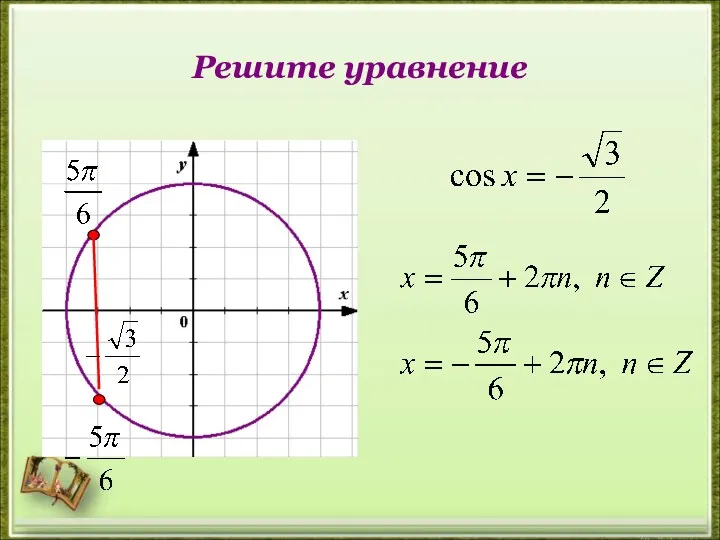
- 14. Решите уравнение
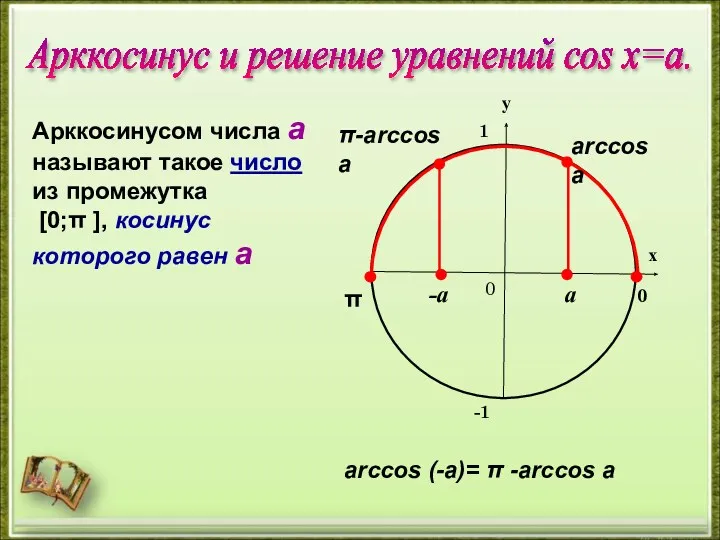
- 15. π 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;π ], косинус которого
- 16. Решим при помощи числовой окружности уравнение cos х = a. 1) Нет точек пересечения с окружностью.
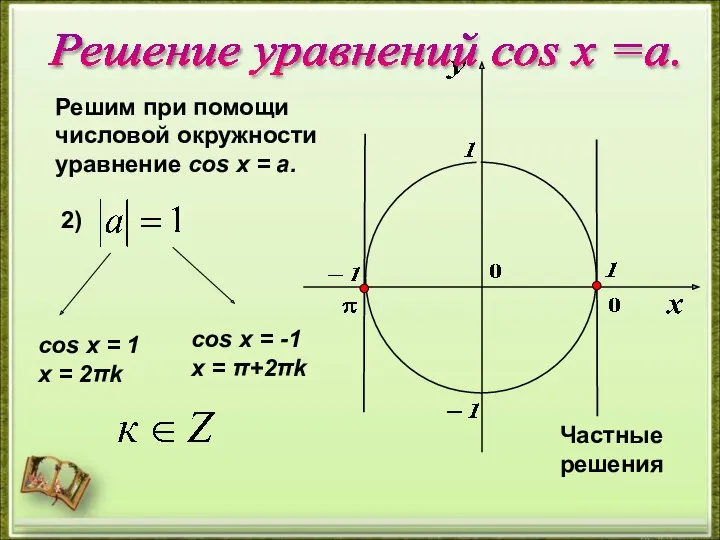
- 17. Решим при помощи числовой окружности уравнение cos х = a. 2) cos х = 1 х
- 18. Решим при помощи числовой окружности уравнение cos х = a. 3) а = 0 Частное решение
- 19. Решим при помощи числовой окружности уравнение cos х = a. 4) Общее решение arccos а -arccos
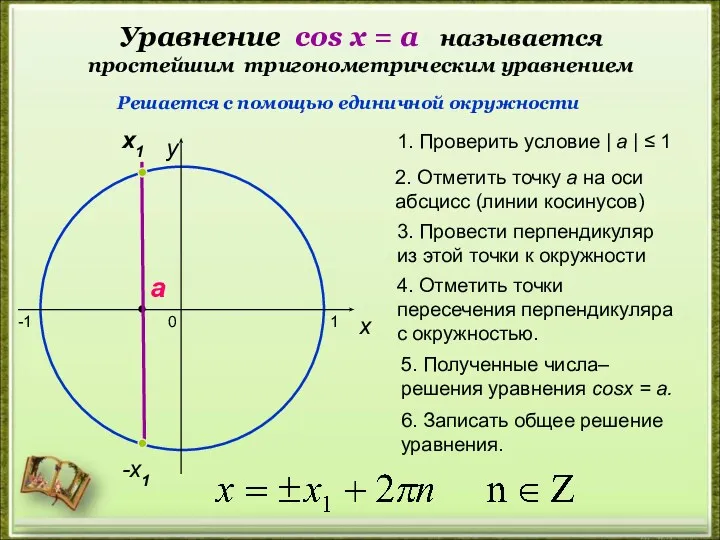
- 20. Уравнение cos х = a называется простейшим тригонометрическим уравнением 0 x y 2. Отметить точку а
- 21. Уравнение cos t = a a) при -1 t1 = arсcos a + 2πk, k ϵ
- 22. Решите уравнение 1) cos х = 2) cos х = -
- 23. Решите уравнение 3) cos 4x = 1 4x = 2πn, n ϵ Z 4)
- 24. Решите уравнение 5) .
- 25. Уравнение sin t = a a) при -1 t1 = arсsin a + 2πn, n ϵ
- 26. Решите уравнение sin х = , , x = ( -1)k + πk, k ϵ Z
- 27. Решите уравнение 2) sin х = - x = ( -1)k+1 ; , , ; x
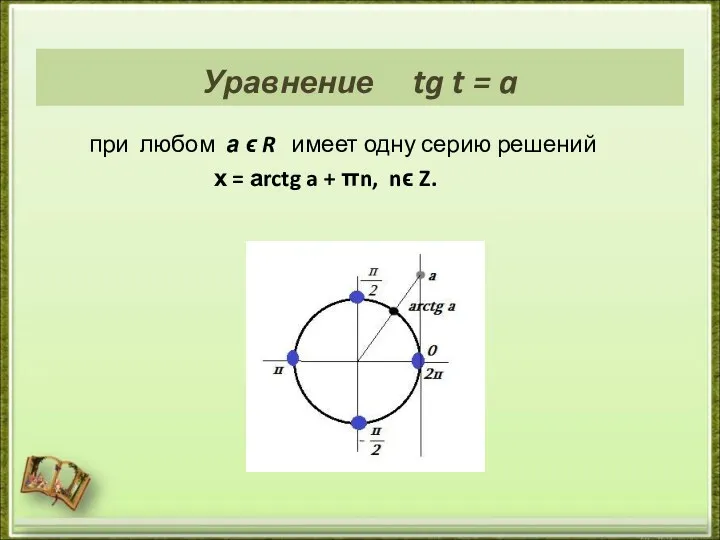
- 28. Уравнение tg t = a при любом а ϵ R имеет одну серию решений х =
- 29. Уравнение ctg t = a при любом а ϵ R имеет одну серию решений х =
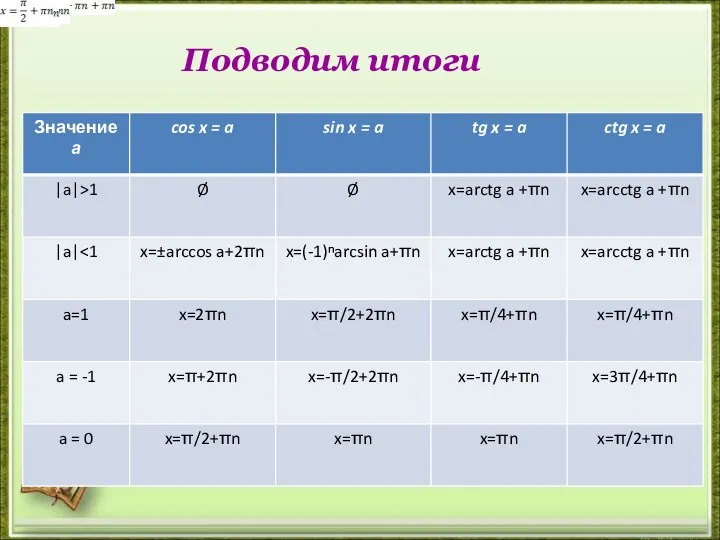
- 30. Подводим итоги
- 32. Скачать презентацию




















 Оптимизация природопользования
Оптимизация природопользования Морское путешествие-2.Счет в пределах 20,вычитание 1 класс
Морское путешествие-2.Счет в пределах 20,вычитание 1 класс Прогрессия. Задачи с решениями
Прогрессия. Задачи с решениями Сложение отрицательных чисел
Сложение отрицательных чисел Урок математики в 1 классе по теме: Число и цифра 7 УМК Перспектива
Урок математики в 1 классе по теме: Число и цифра 7 УМК Перспектива Объемы тел. Решение задач
Объемы тел. Решение задач Тест Решение задач по теме Сложение и вычитание круглых сотен, 2 класс
Тест Решение задач по теме Сложение и вычитание круглых сотен, 2 класс Смешанные числа. Ребус
Смешанные числа. Ребус Чтение графиков и диаграмм
Чтение графиков и диаграмм Счёт предметов.
Счёт предметов. презентация по математике на тему: Измеряем время
презентация по математике на тему: Измеряем время Деление обыкновенных дробей
Деление обыкновенных дробей Теорема о площади треугольника
Теорема о площади треугольника Луч, прямая, отрезок.
Луч, прямая, отрезок. Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости
Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости Radix sort
Radix sort Координатная плоскость. 7 класс
Координатная плоскость. 7 класс Повторення вивченого. Запис та складання виразів. Робота над задачами. Геометричний матеріал. Урок №66
Повторення вивченого. Запис та складання виразів. Робота над задачами. Геометричний матеріал. Урок №66 Подготовка к ЕГЭ. Площади фигур
Подготовка к ЕГЭ. Площади фигур Определение квадратичной функции
Определение квадратичной функции Сложение чисел с разными знаками
Сложение чисел с разными знаками Множества. Отношения между множествами
Множества. Отношения между множествами Степень с натуральным показателем и ее свойства
Степень с натуральным показателем и ее свойства Решение задач по теме Подобные слагаемые
Решение задач по теме Подобные слагаемые Число 7. Презентация к уроку математики в 1 классе.
Число 7. Презентация к уроку математики в 1 классе. Прямоугольный параллелепипед
Прямоугольный параллелепипед Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Число ноль
Число ноль