Содержание
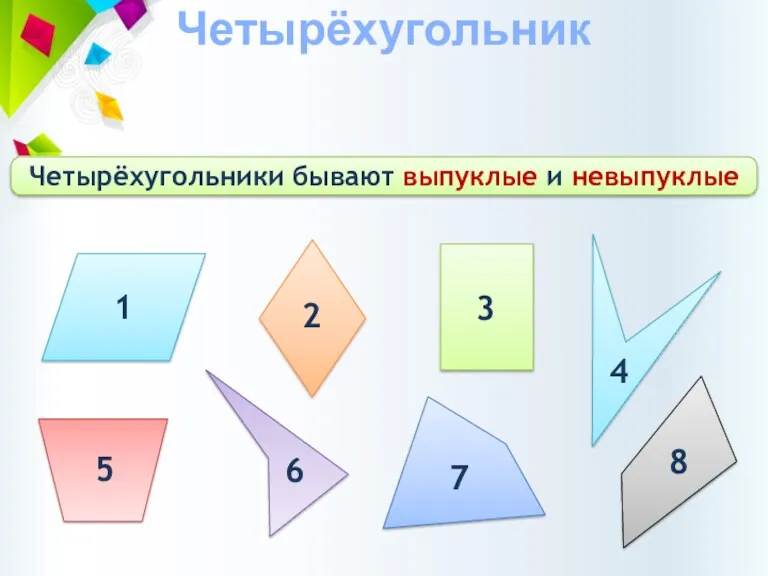
- 2. Четырёхугольник Четырёхугольники бывают выпуклые и невыпуклые
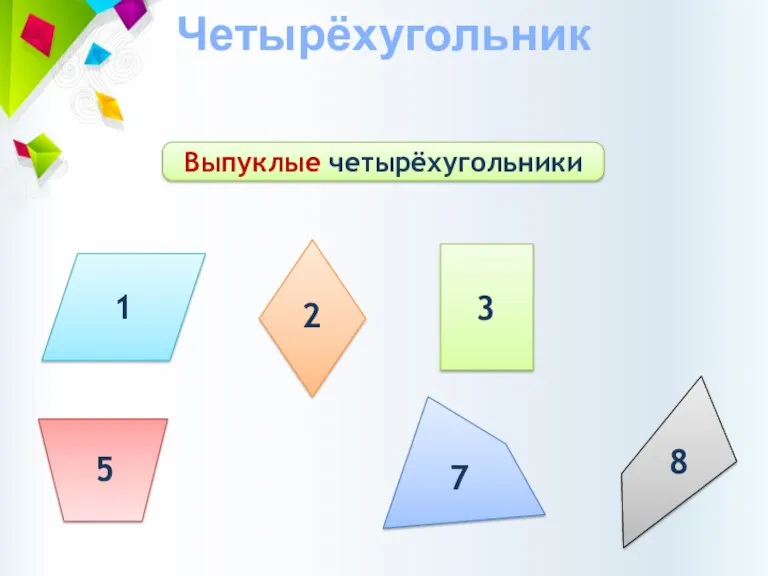
- 3. Четырёхугольник Выпуклые четырёхугольники
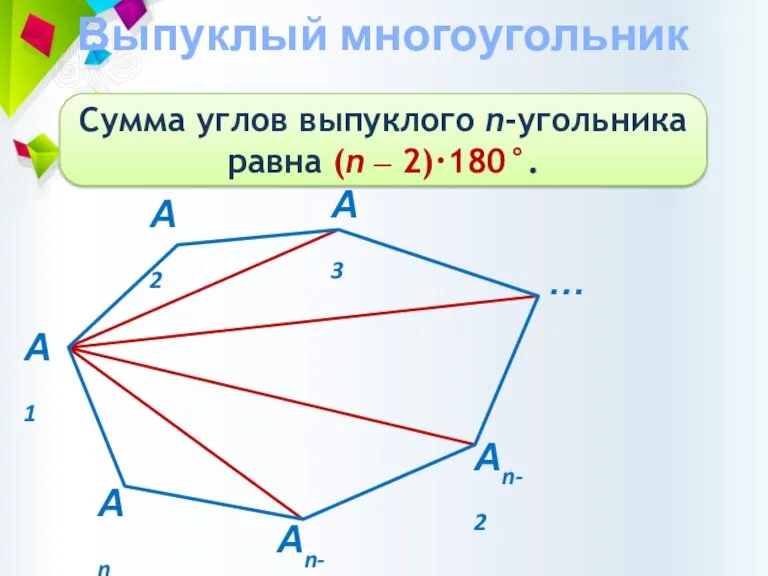
- 4. Выпуклый многоугольник Сумма углов выпуклого n-угольника равна (n ‒ 2)·180°.
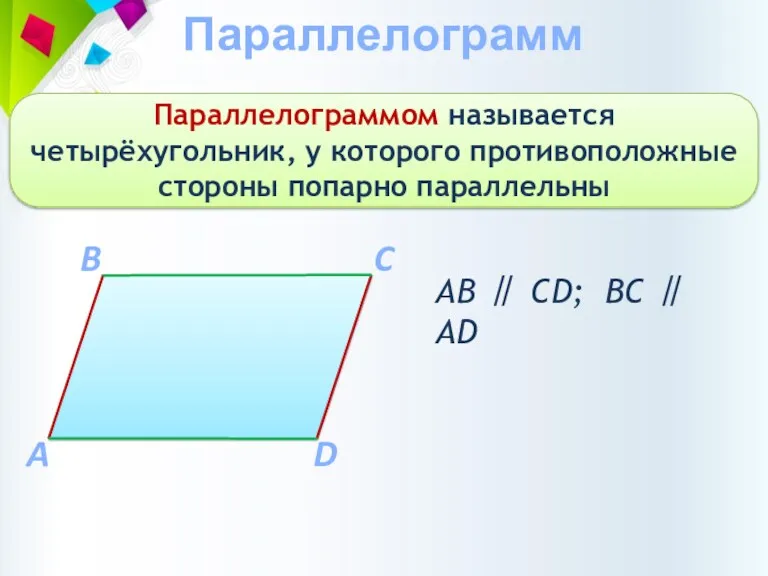
- 5. Параллелограмм Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны A C B D АВ ∥
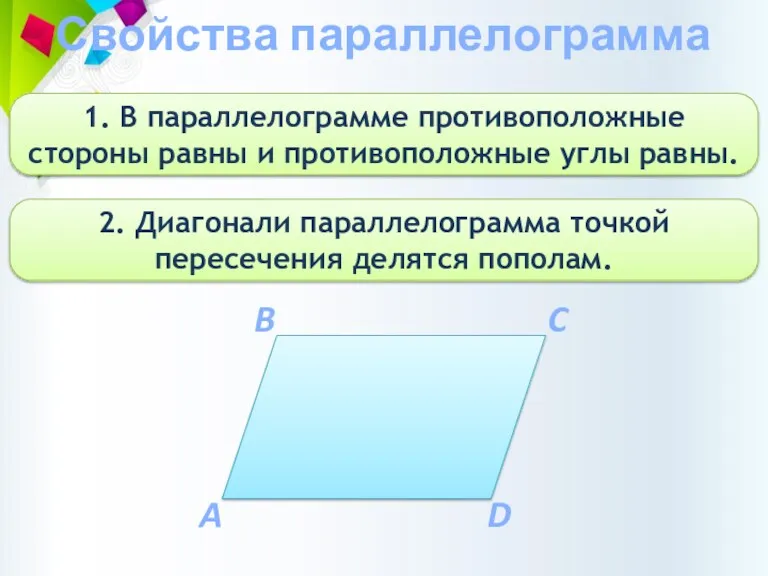
- 6. Свойства параллелограмма 1. В параллелограмме противоположные стороны равны и противоположные углы равны. 2. Диагонали параллелограмма точкой
- 7. Признаки параллелограмма 1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник ‒ параллелограмм.
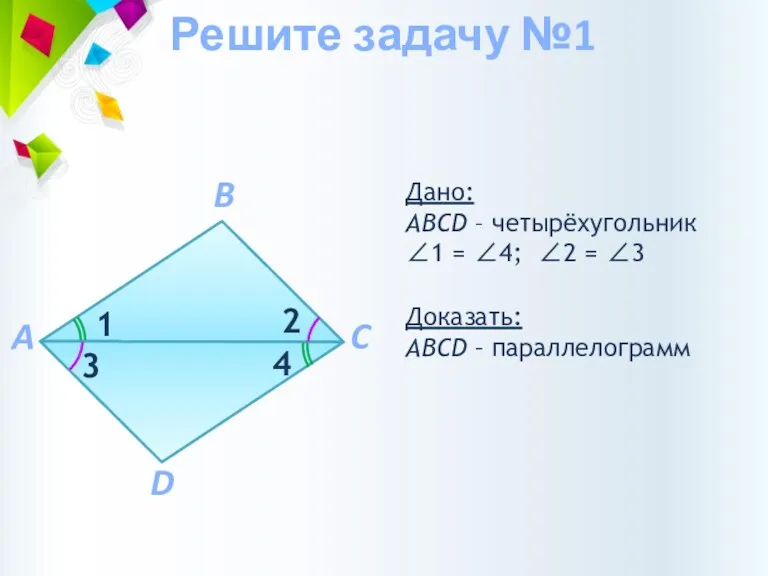
- 8. Доказать: АВCD – параллелограмм Дано: АВCD – четырёхугольник ∠1 = ∠4; ∠2 = ∠3 Решите задачу
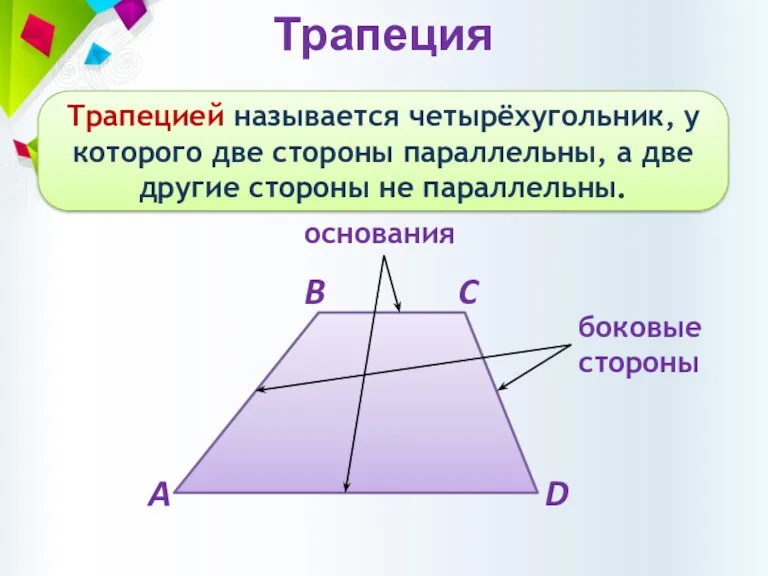
- 9. Трапеция Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. основания
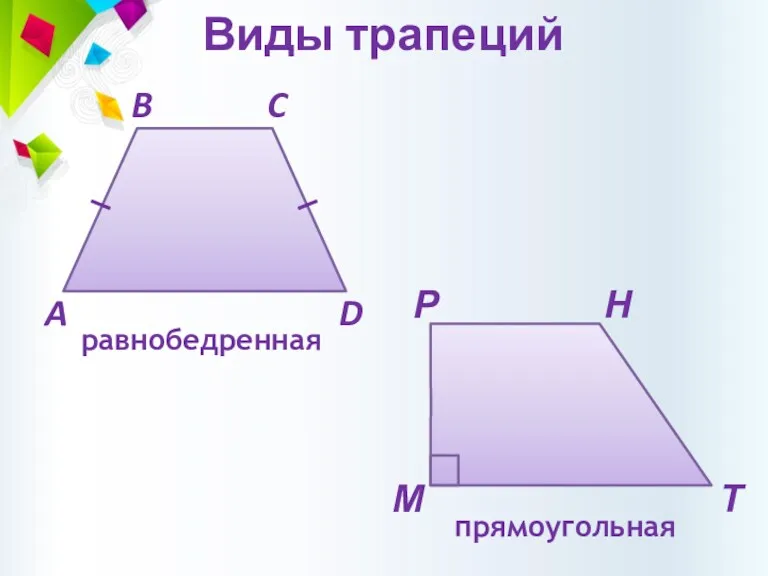
- 10. Виды трапеций прямоугольная равнобедренная
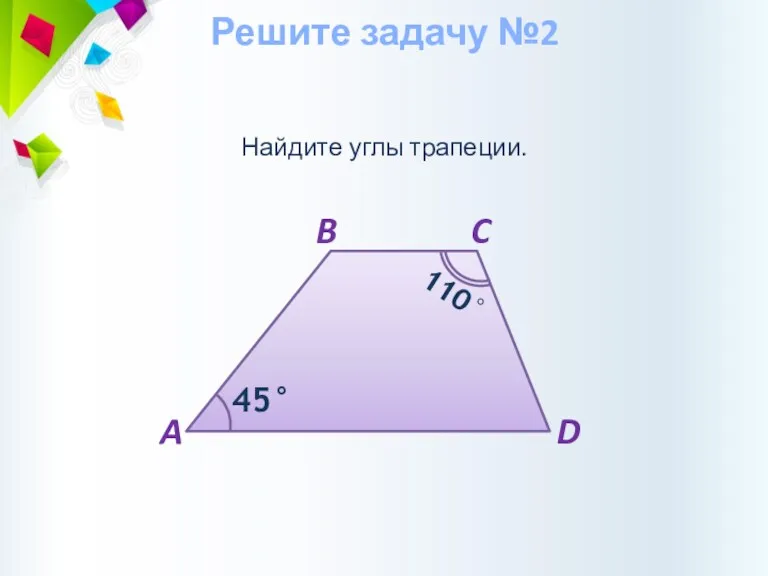
- 11. Найдите углы трапеции. Решите задачу №2
- 12. Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые A C B D ∠А=∠В=∠С=∠D=90° АВ ∥
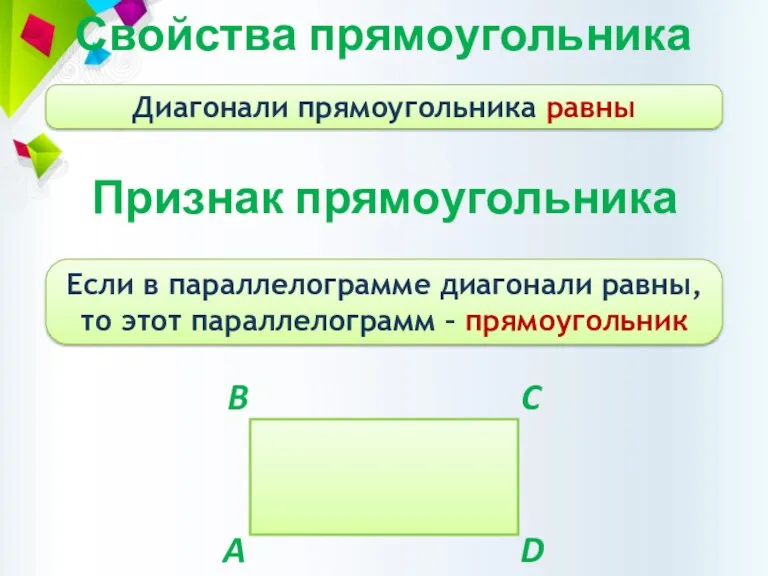
- 13. Свойства прямоугольника Диагонали прямоугольника равны Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм –
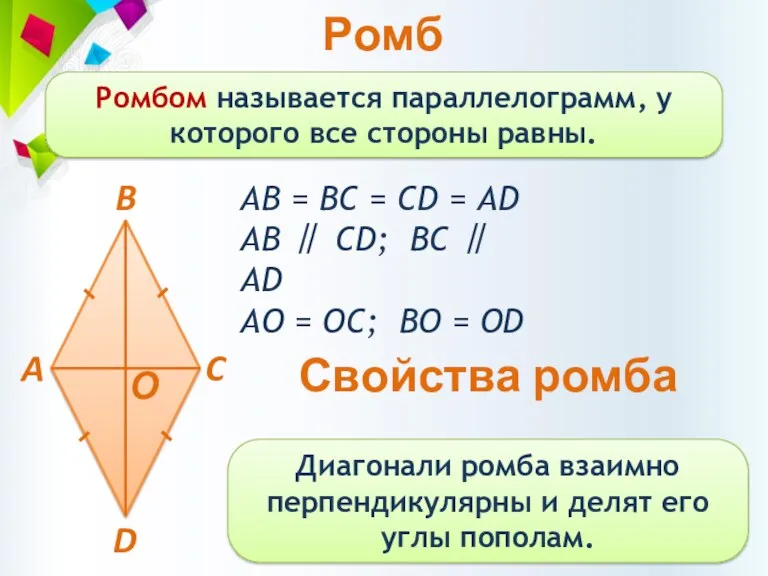
- 14. Ромб Ромбом называется параллелограмм, у которого все стороны равны. АВ = BC = CD = AD
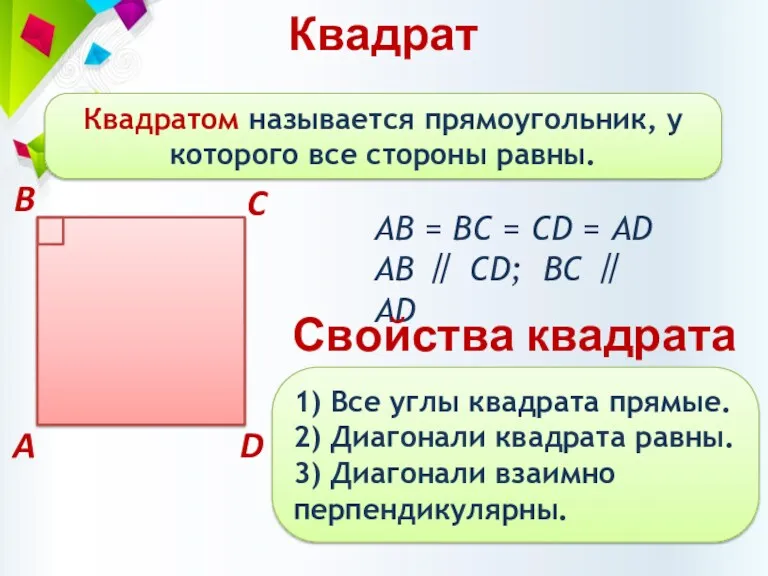
- 15. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. АВ = BC = CD = AD
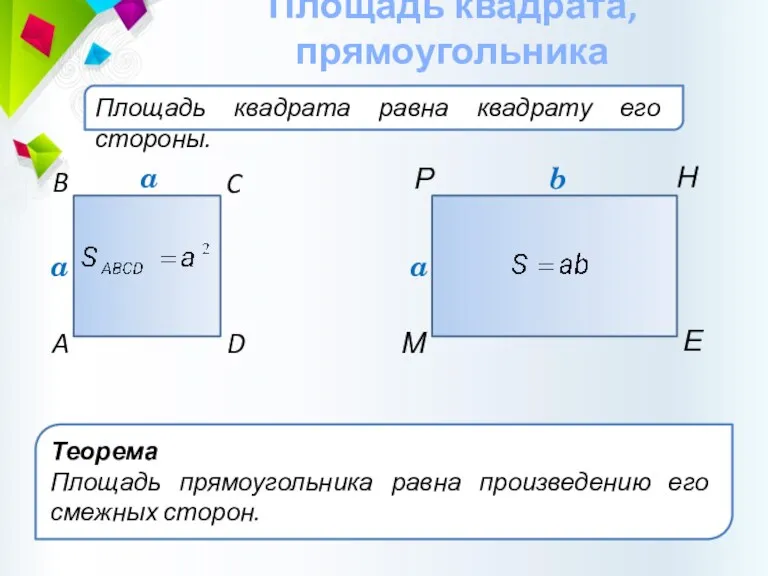
- 16. Площадь квадрата равна квадрату его стороны. Площадь квадрата, прямоугольника C B D A a Теорема Площадь
- 17. Дано: ABCD – прямоугольник ∠1 = ∠2, BP = 7, РC = 5 Найти: SABCD P
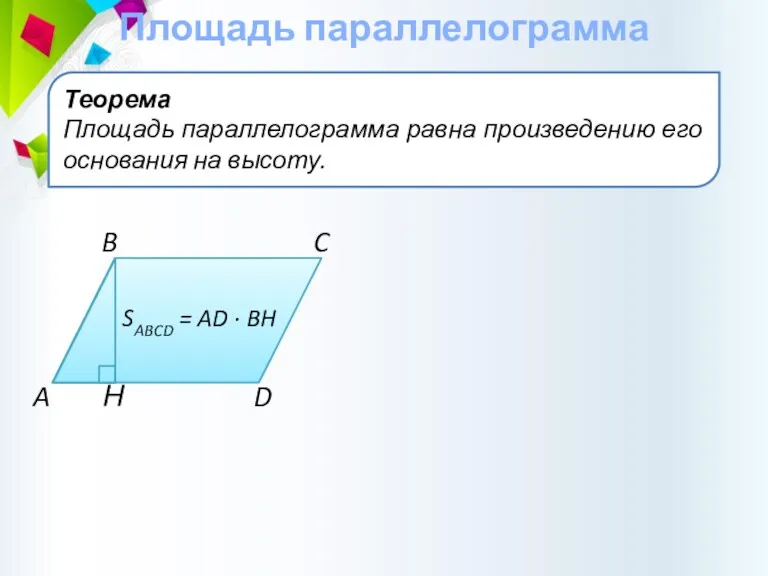
- 18. Теорема Площадь параллелограмма равна произведению его основания на высоту. Площадь параллелограмма C B D A Н
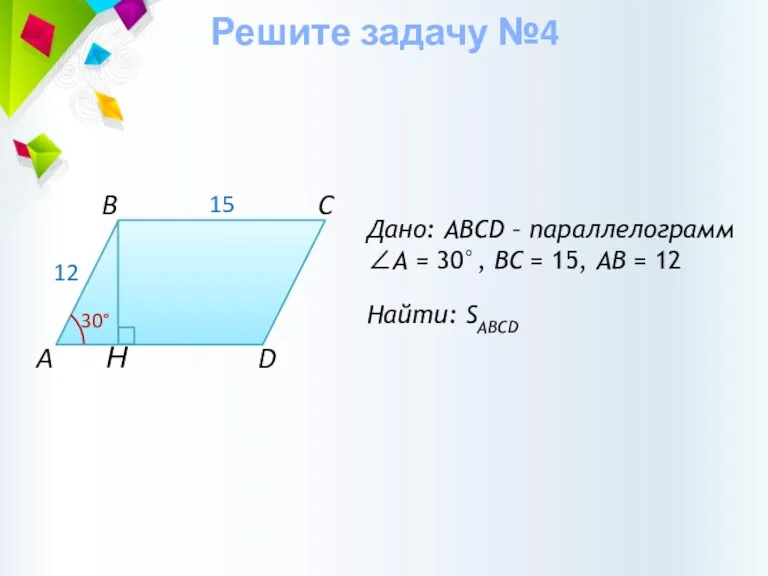
- 19. Н Дано: ABCD – параллелограмм ∠А = 30°, BС = 15, АВ = 12 Найти: SABCD
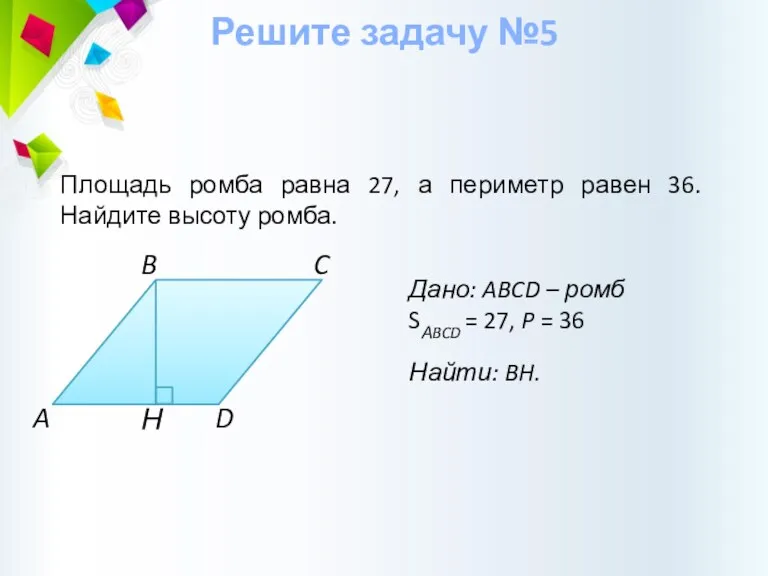
- 20. Н Дано: ABCD – ромб SАBCD = 27, P = 36 Найти: BH. Решите задачу №5
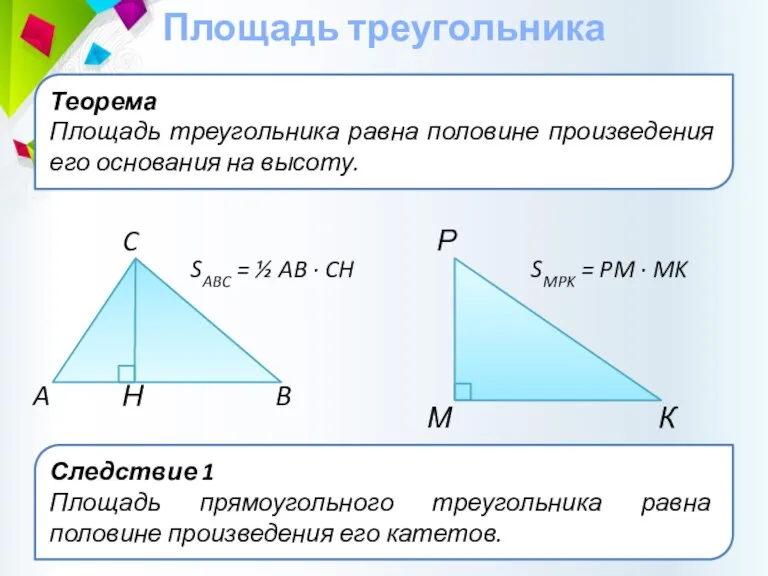
- 21. Теорема Площадь треугольника равна половине произведения его основания на высоту. Площадь треугольника C B A Н
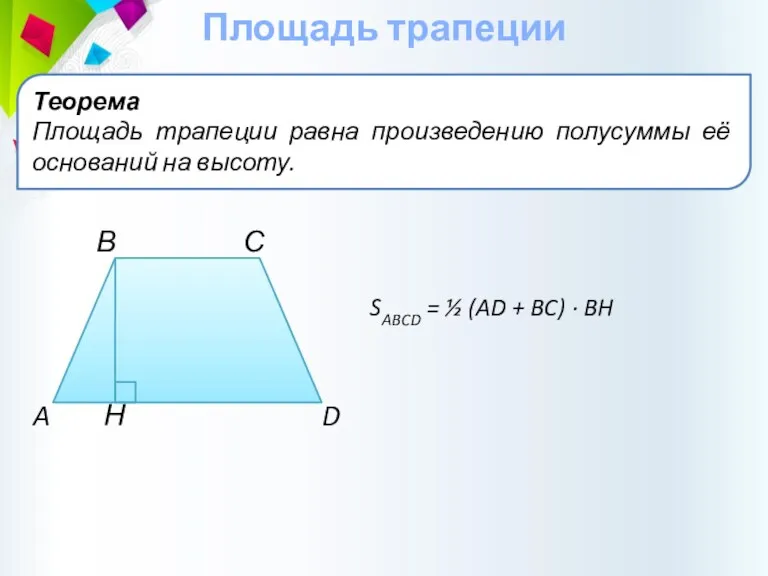
- 22. Площадь трапеции Теорема Площадь трапеции равна произведению полусуммы её оснований на высоту. В С A Н
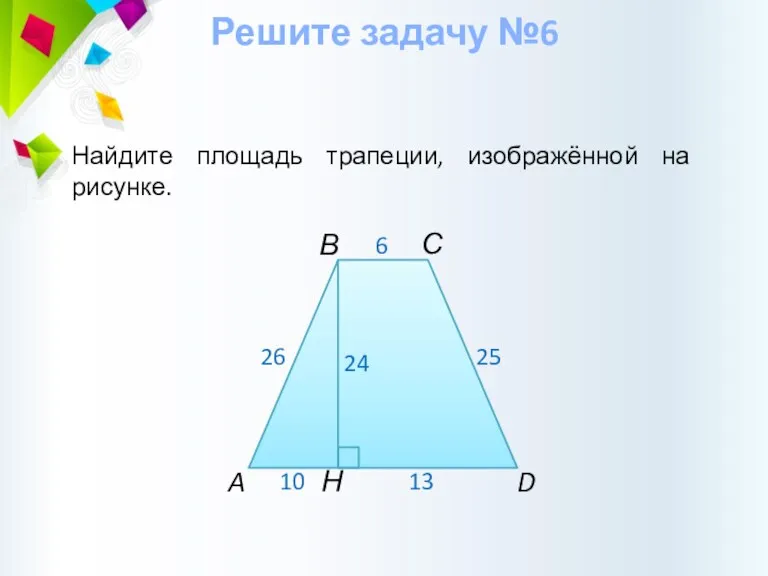
- 23. Решите задачу №6 Найдите площадь трапеции, изображённой на рисунке.
- 24. Теорема Пифагора c2 = a2 + b2 c b В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 25. Первый признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого, то такие
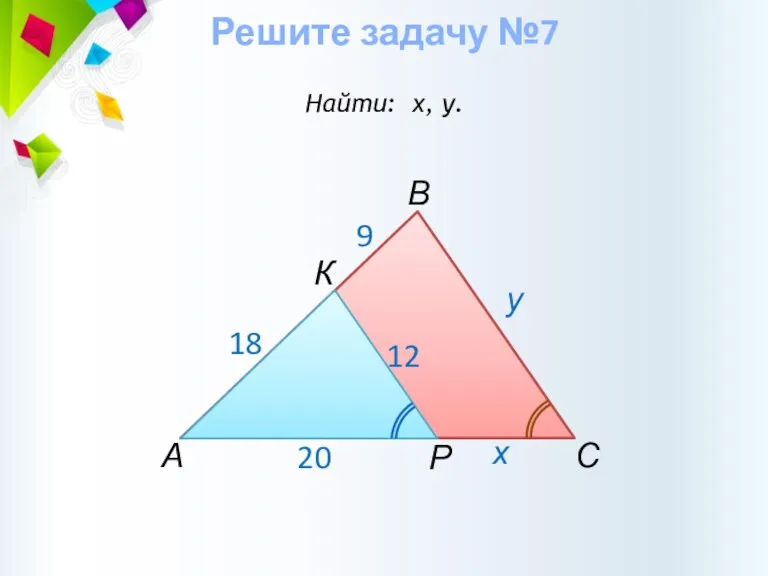
- 26. Решите задачу №7 Найти: х, у. А В С у х Р К 18 20 9
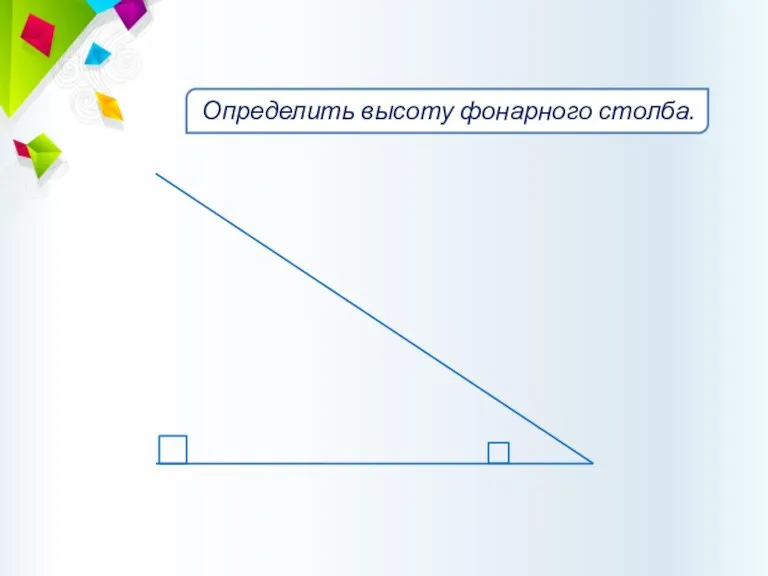
- 27. Определить высоту фонарного столба. Решите задачу №8
- 28. Синус острого угла прямоугольного треугольника Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
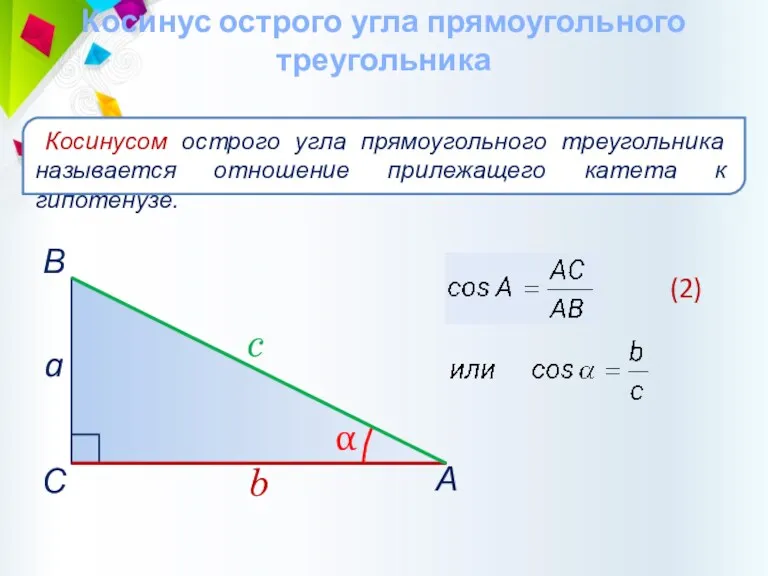
- 29. Косинус острого угла прямоугольного треугольника Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
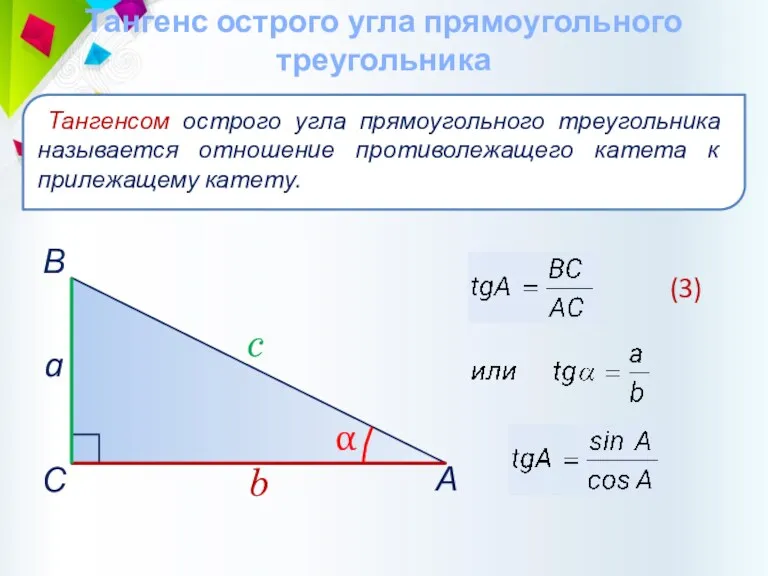
- 30. Тангенс острого угла прямоугольного треугольника Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
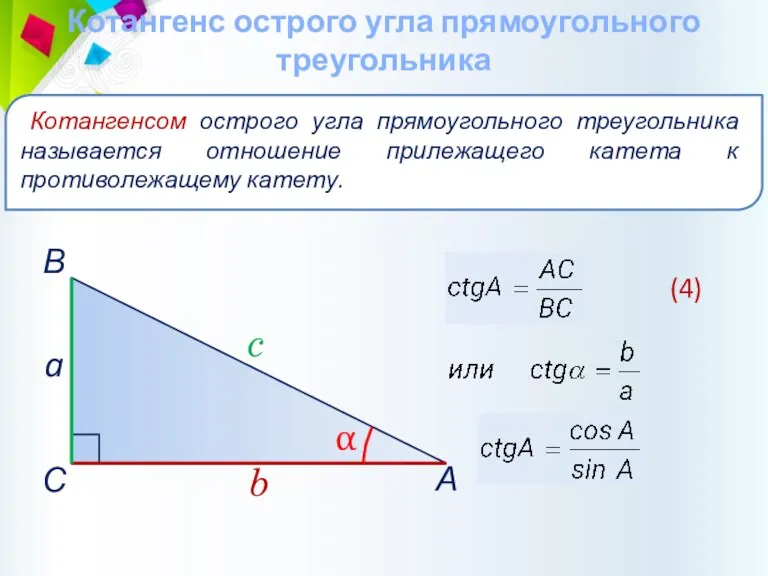
- 31. Котангенс острого угла прямоугольного треугольника Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
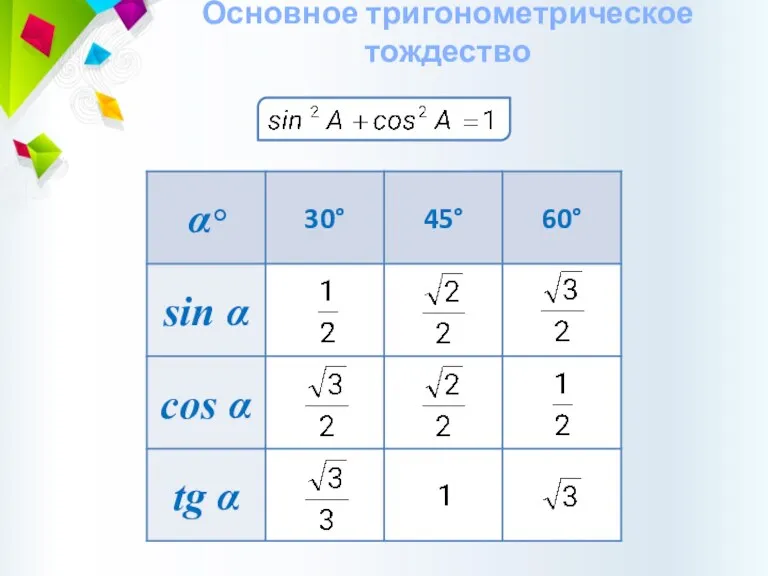
- 32. Основное тригонометрическое тождество
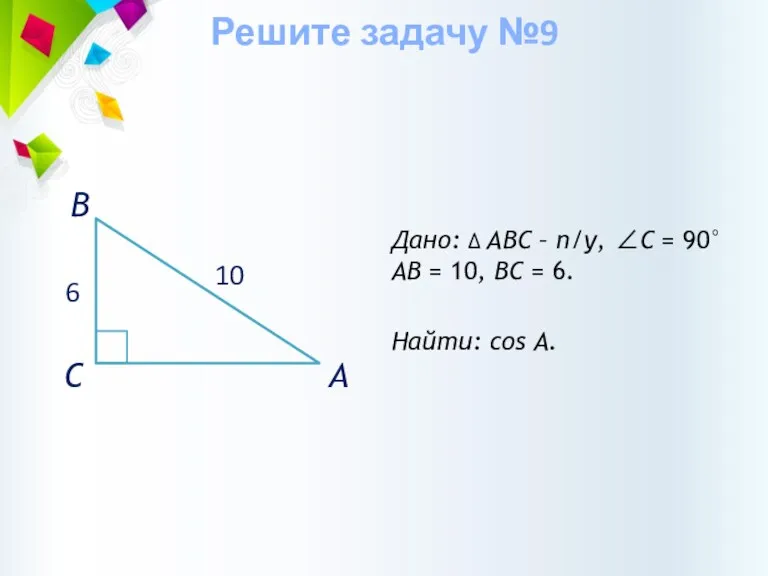
- 33. Дано: ∆ АВС – п/у, ∠С = 90° АВ = 10, ВС = 6. Найти: cos
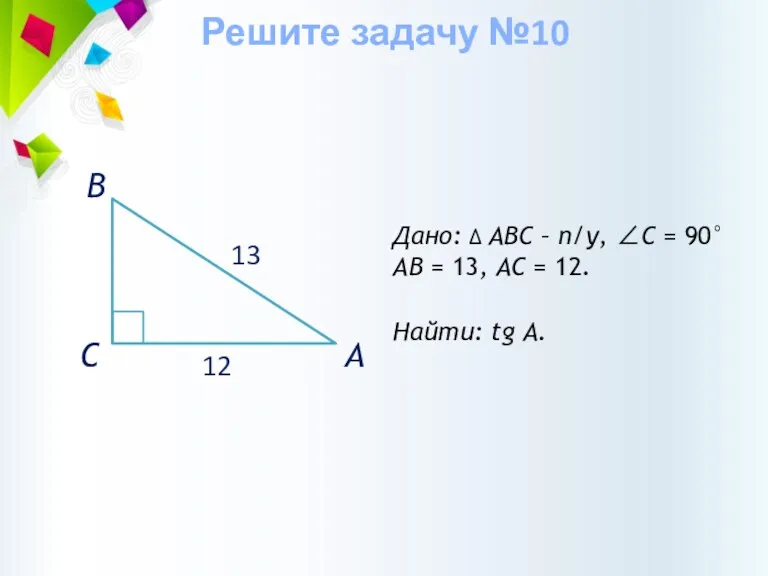
- 34. Дано: ∆ АВС – п/у, ∠С = 90° АВ = 13, АС = 12. Найти: tg
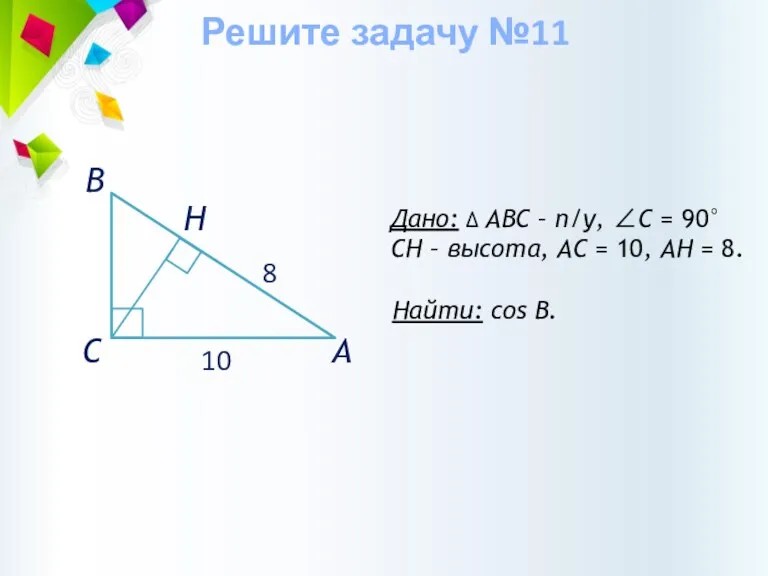
- 35. Дано: ∆ АВС – п/у, ∠С = 90° CH – высота, АС = 10, АН =
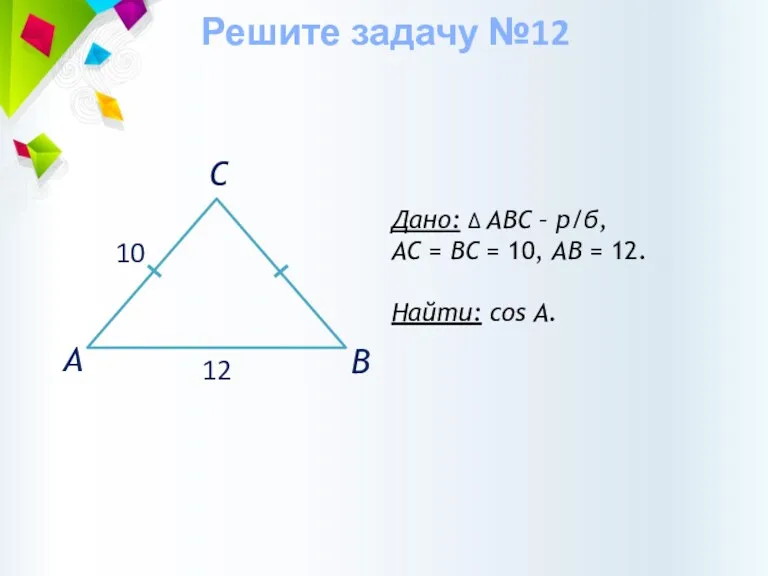
- 36. Дано: ∆ АВС – р/б, АС = ВС = 10, АВ = 12. Найти: cos А.
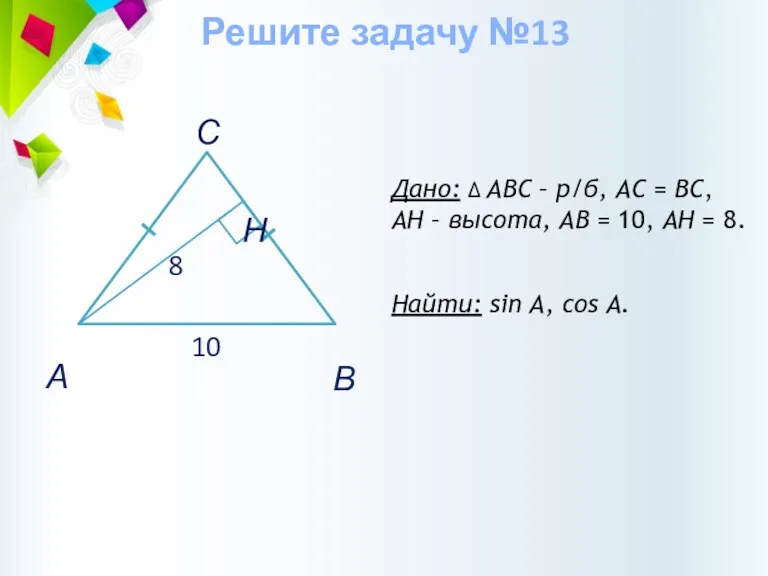
- 37. Дано: ∆ АВС – р/б, АС = ВС, AH – высота, АВ = 10, AH =
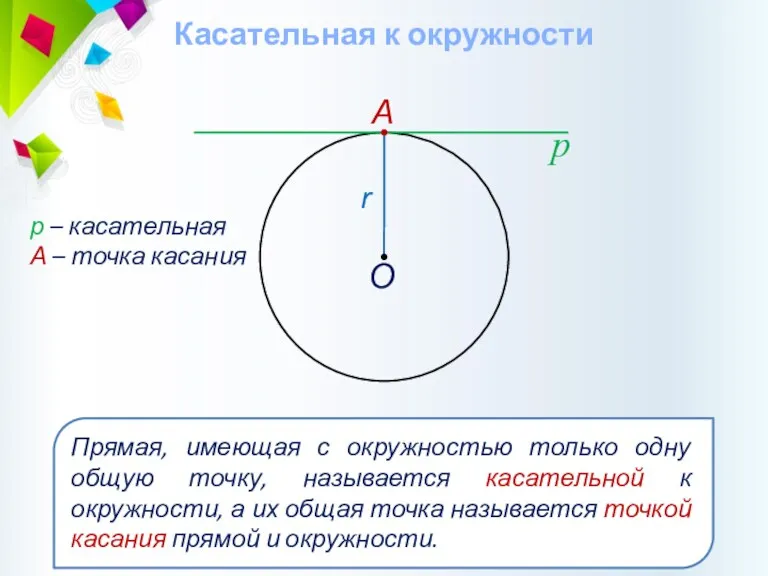
- 38. Касательная к окружности р р – касательная А – точка касания А О Прямая, имеющая с
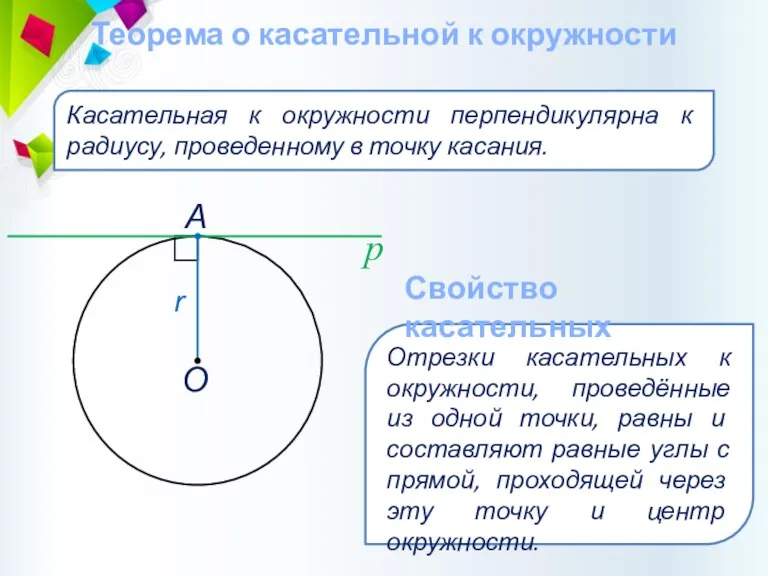
- 39. Теорема о касательной к окружности Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Отрезки
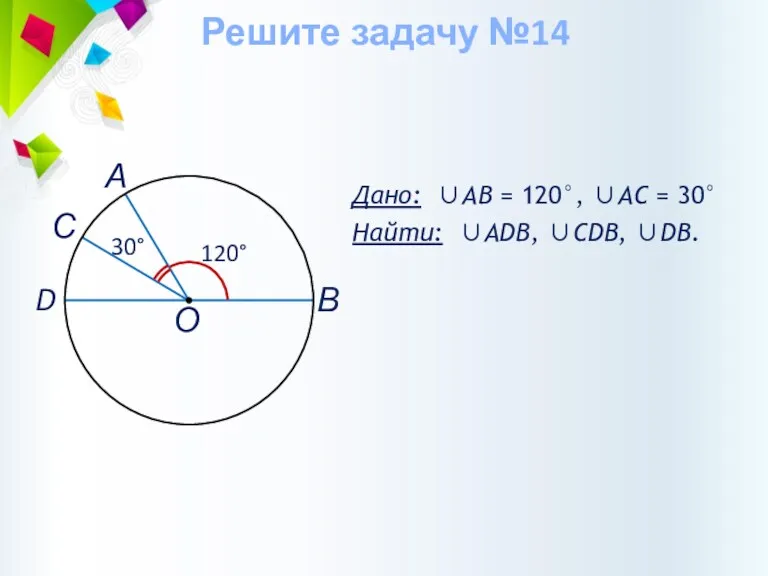
- 40. Дано: ∪АВ = 120°, ∪AC = 30° Найти: ∪АDВ, ∪CDB, ∪DB. Решите задачу №14
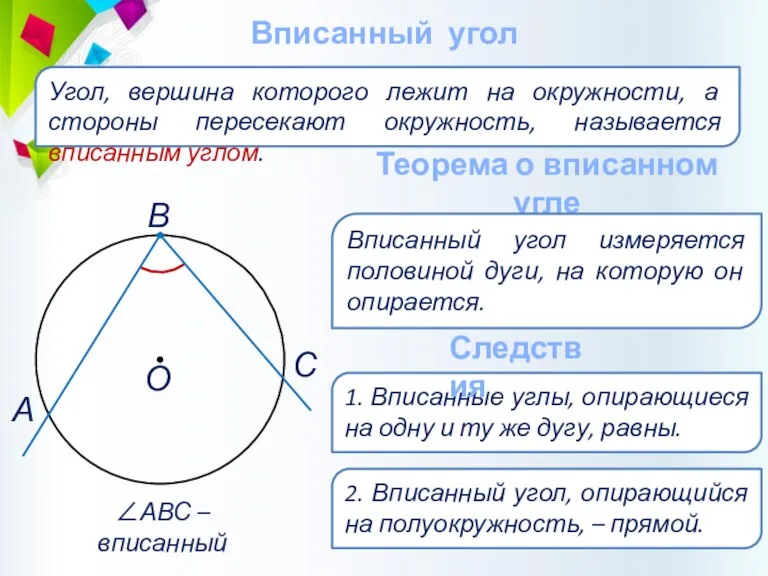
- 41. Вписанный угол Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. ∠АВС
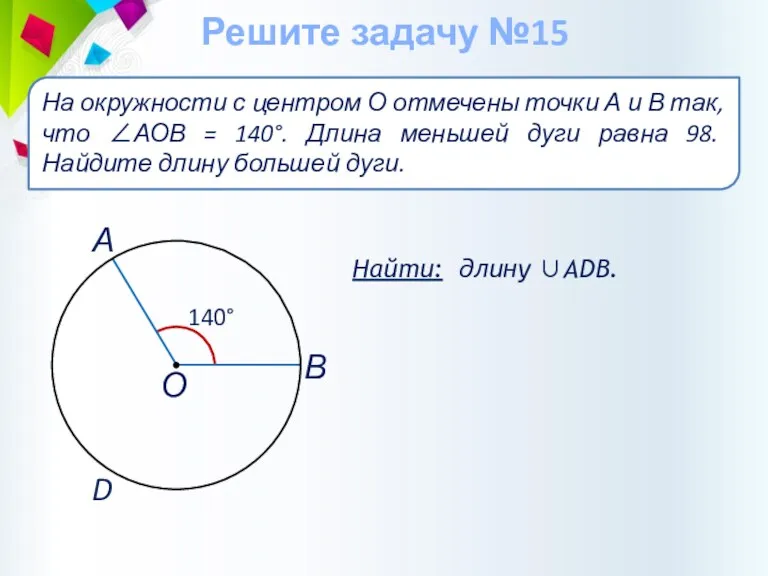
- 42. Найти: длину ∪АDВ. На окружности с центром О отмечены точки А и В так, что ∠АОВ
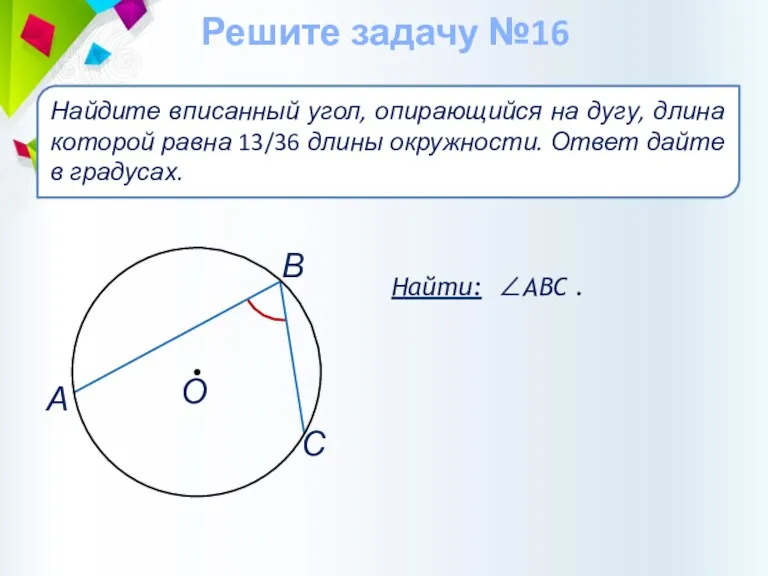
- 43. Найти: ∠АВС . Найдите вписанный угол, опирающийся на дугу, длина которой равна 13/36 длины окружности. Ответ
- 44. Свойство биссектрисы Теорема. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: Каждая точка, лежащая
- 45. Следствие: Биссектрисы треугольника пересекаются в одной точке.
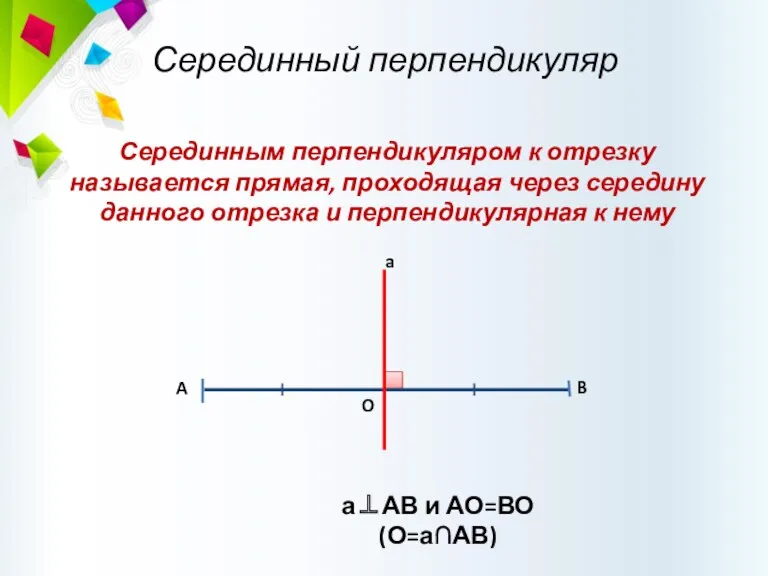
- 46. Серединный перпендикуляр Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к
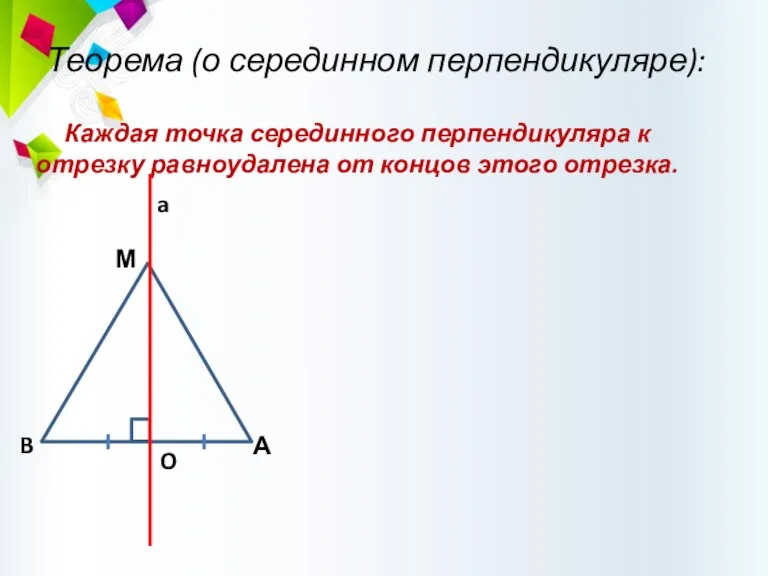
- 47. Теорема (о серединном перпендикуляре): Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
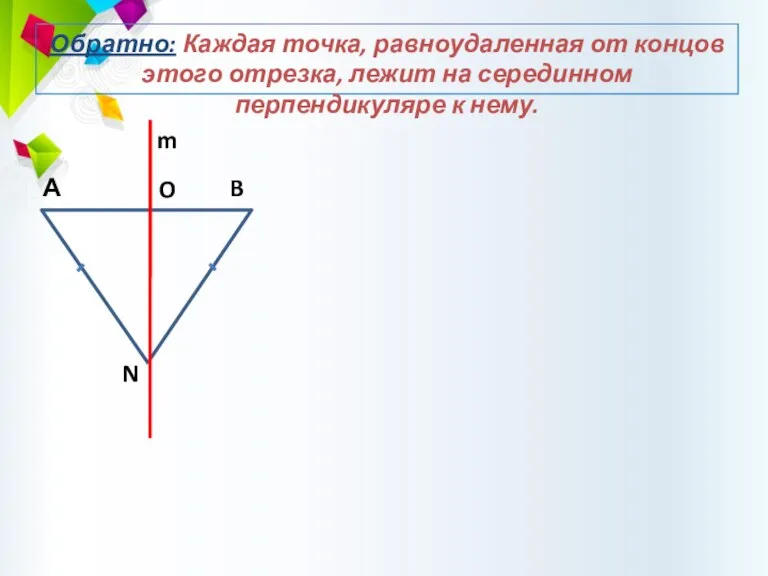
- 48. Обратно: Каждая точка, равноудаленная от концов этого отрезка, лежит на серединном перпендикуляре к нему.
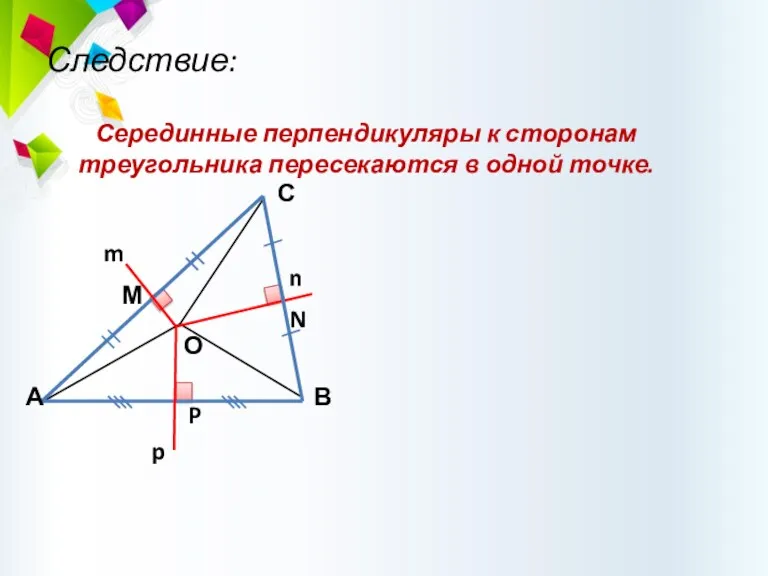
- 49. Следствие: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
- 50. Высоты треугольника (или их продолжения) пересекаются в одной точке.
- 51. Вписанная окружность
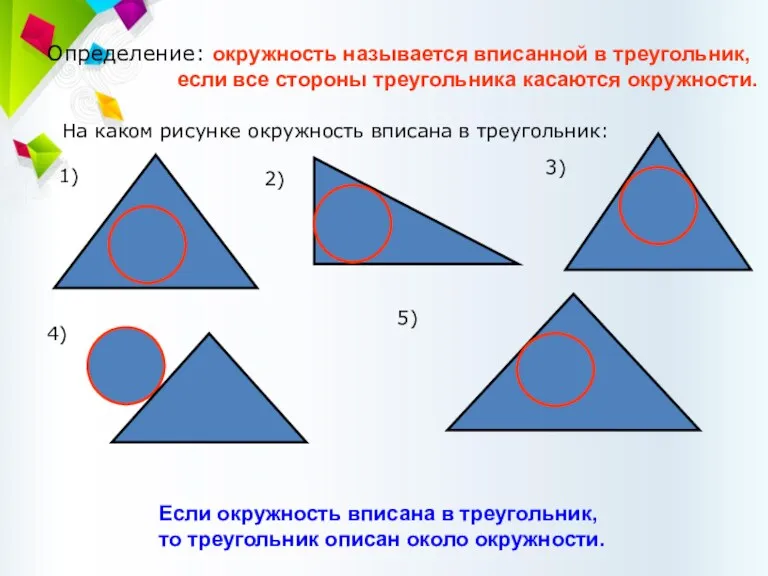
- 52. Определение: окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. Если окружность вписана в
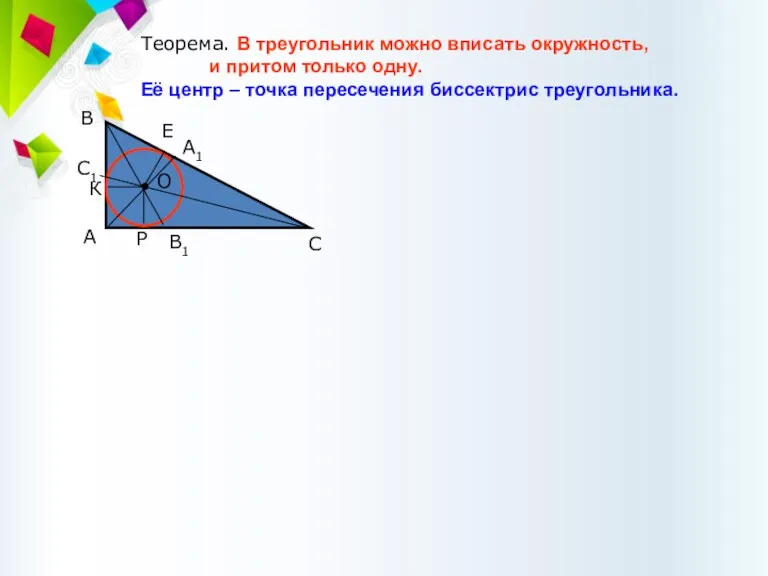
- 53. Теорема. В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис
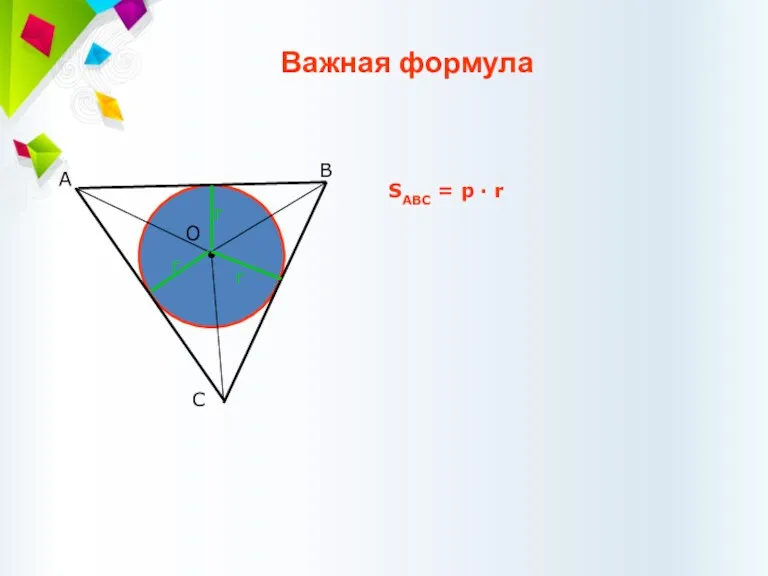
- 54. Важная формула SABC = p · r
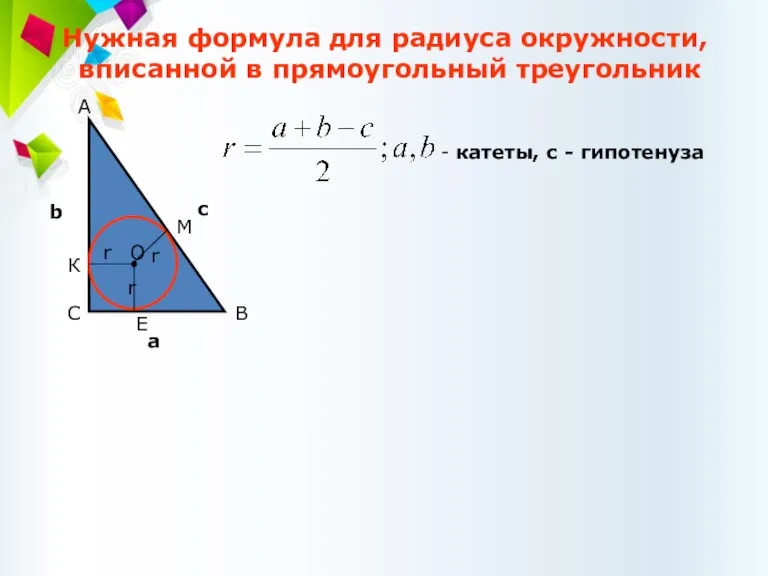
- 55. Нужная формула для радиуса окружности, вписанной в прямоугольный треугольник
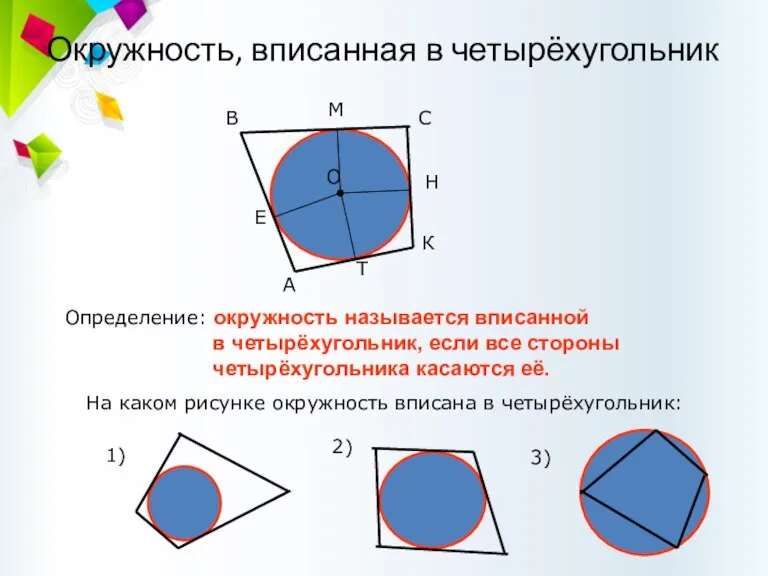
- 56. Окружность, вписанная в четырёхугольник Определение: окружность называется вписанной в четырёхугольник, если все стороны четырёхугольника касаются её.
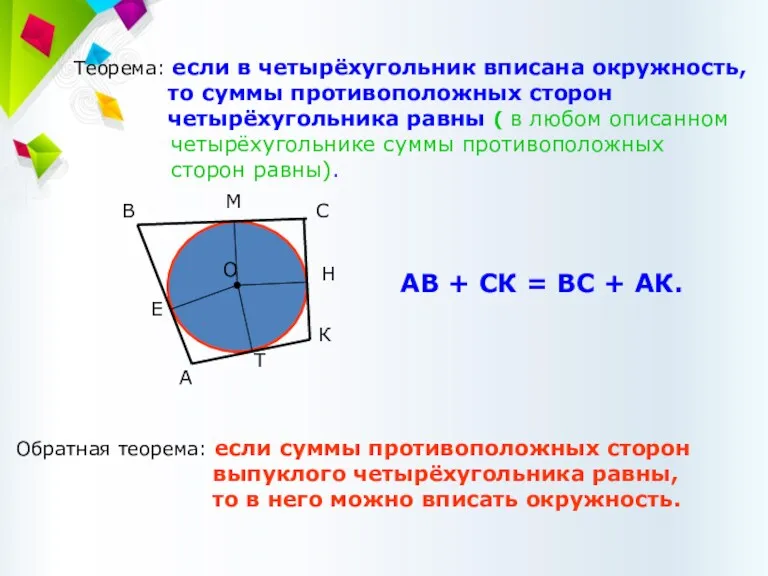
- 57. Теорема: если в четырёхугольник вписана окружность, то суммы противоположных сторон четырёхугольника равны ( в любом описанном
- 58. Описанная окружность
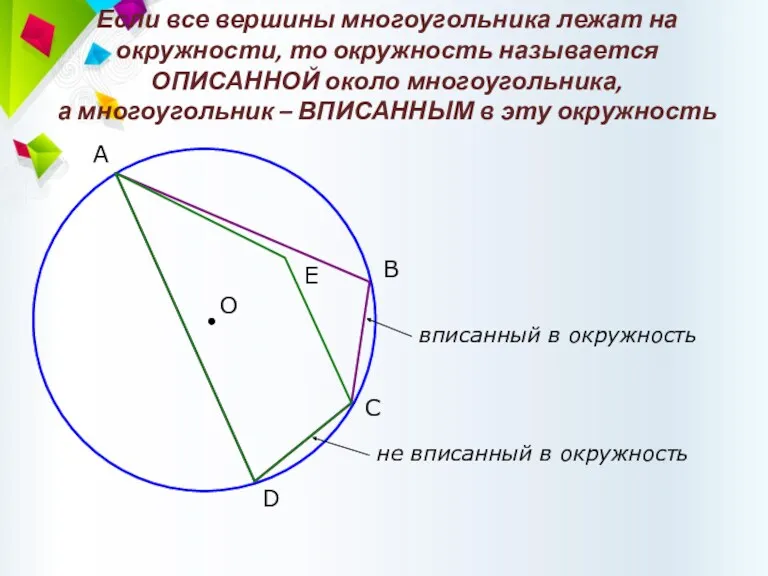
- 59. Если все вершины многоугольника лежат на окружности, то окружность называется ОПИСАННОЙ около многоугольника, а многоугольник –
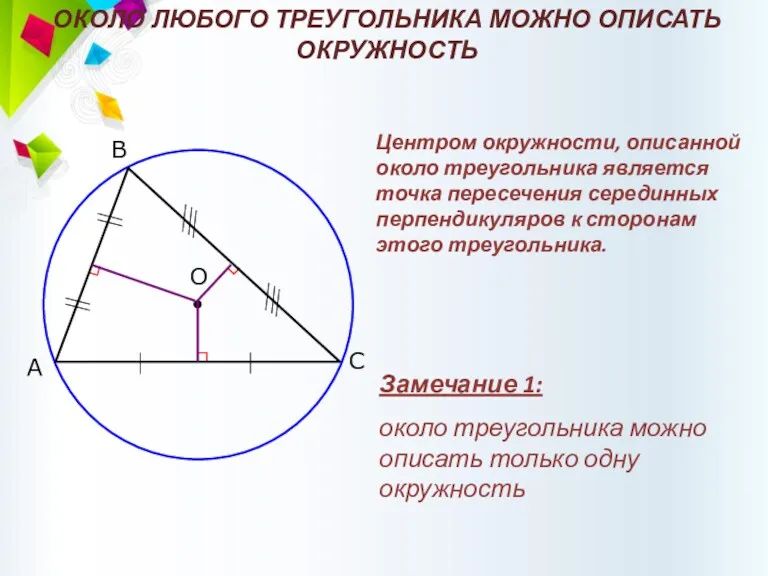
- 60. ОКОЛО ЛЮБОГО ТРЕУГОЛЬНИКА МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ В С А Замечание 1: около треугольника можно описать только
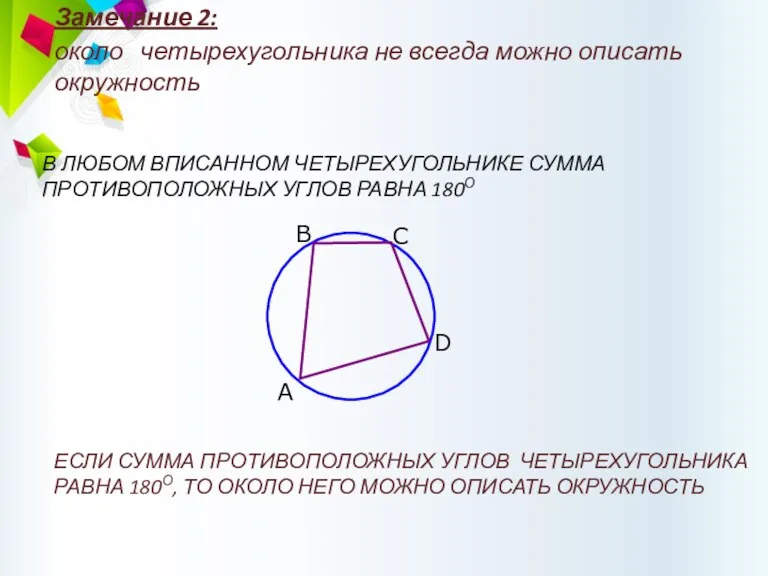
- 61. Замечание 2: около четырехугольника не всегда можно описать окружность В ЛЮБОМ ВПИСАННОМ ЧЕТЫРЕХУГОЛЬНИКЕ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ
- 63. Скачать презентацию











 Парная линейная регрессия в экономике
Парная линейная регрессия в экономике Действия с натуральными числами
Действия с натуральными числами Конспект урока математики 3 класс Закрепление темы: Таблица умножения на 2,3,4,5,6. Решение задач
Конспект урока математики 3 класс Закрепление темы: Таблица умножения на 2,3,4,5,6. Решение задач Применение различных способов разложения многочлена на множители. 7 класс
Применение различных способов разложения многочлена на множители. 7 класс Сложение числа б с однозначными числами. 1 класс
Сложение числа б с однозначными числами. 1 класс Векторы в пространстве
Векторы в пространстве Математика, 4 класс. Тема: Углы. Виды углов
Математика, 4 класс. Тема: Углы. Виды углов Треугольники. Виды треугольников. Признаки равенства треугольников
Треугольники. Виды треугольников. Признаки равенства треугольников Внеклассное мероприятие по математике: Своя игра
Внеклассное мероприятие по математике: Своя игра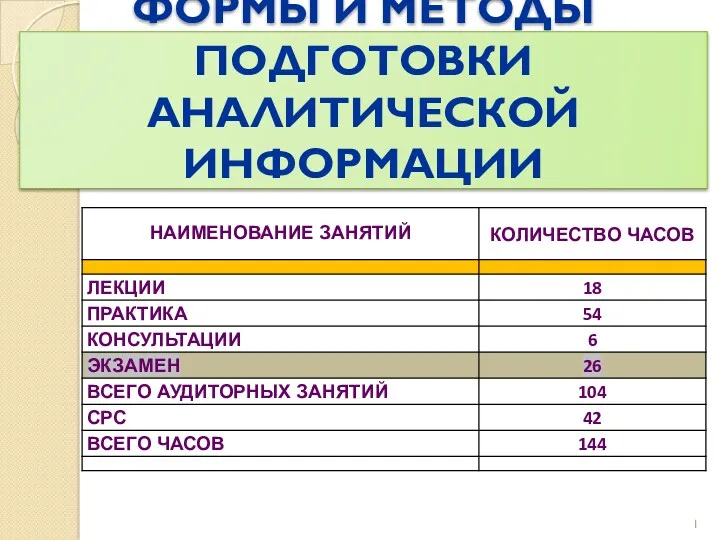 Формы и методы подготовки аналитической информации
Формы и методы подготовки аналитической информации Сечение поверхности плоскостью. (Лекция 6)
Сечение поверхности плоскостью. (Лекция 6) Виды углов. Измерение углов. 5 класс
Виды углов. Измерение углов. 5 класс Тікбұрышты параллелепипед көлемі
Тікбұрышты параллелепипед көлемі Презентация к уроку математики по теме: Нахождение неизвестного множителя. 3 класс УМК Перспективная начальная школа
Презентация к уроку математики по теме: Нахождение неизвестного множителя. 3 класс УМК Перспективная начальная школа Дроби и проценты. Нахождение процента от величины
Дроби и проценты. Нахождение процента от величины Площадь. Свойства площади. Формула площади прямоугольника
Площадь. Свойства площади. Формула площади прямоугольника Моделирование систем и процессов. Теория графов. (Лекция 2)
Моделирование систем и процессов. Теория графов. (Лекция 2) Двугранный угол
Двугранный угол Тест. Таблица умножения.
Тест. Таблица умножения. Текстовые задачи и пути их решения. Элективный курс. 9 класс
Текстовые задачи и пути их решения. Элективный курс. 9 класс Презентация. Математика. Умножение
Презентация. Математика. Умножение Способы доказательства теоремы Пифагора
Способы доказательства теоремы Пифагора Признак перпендикулярности прямой и плоскости. (10 класс)
Признак перпендикулярности прямой и плоскости. (10 класс) Презентация к уроку математики Морское путешествие
Презентация к уроку математики Морское путешествие Можно ли без шаблона разметить круг? Циркуль – чертежный инструмент
Можно ли без шаблона разметить круг? Циркуль – чертежный инструмент Урок с применением ИКТ
Урок с применением ИКТ презентация по теме Развитие креативного мышления младших школьников средством дидактических игр на уроках математики в системе развивающего обучения
презентация по теме Развитие креативного мышления младших школьников средством дидактических игр на уроках математики в системе развивающего обучения Обобщение материала по теме Умножение и деление обыкновенных дробей 6 класс
Обобщение материала по теме Умножение и деление обыкновенных дробей 6 класс