Содержание
- 2. Дополнительный теоретический материал В треугольнике со сторонами a, b, c расстояние от вершины А до точек
- 3. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от
- 4. Центр окружности, описанной около трапеции, лежит на пересечении серединных перпендикуляров к сторонам трапеции. При любом способе
- 5. Пересекающиеся в точка А и В окружности имеют общую хорду АВ. Общая хорда перпендикулярна линии центров
- 6. Диагональ параллелограмма разбивает его на два равновеликих треугольника. Трапеция разбивается диагоналями на два равновеликих треугольника (примыкающих
- 7. Прямая, параллельная стороне треугольника и пересекающая две другие, отсекает от него треугольник, подобный данному. Если р
- 8. Опорные задачи Отрезок общей внешней касательной к двум окружностям радиусов R и r равен Пусть в
- 9. ЕГЭ 2010 года • В треугольнике ABC АВ =12, ВС = 5, СА = 10. Точка
- 10. А для окружности вписанной в треугольник ADB Поскольку в условии сказано, что точка D лежит на
- 11. Пусть точка D лежит на отрезке ВС (рис.а). Тогда Значит, 2. Пусть точка D лежит вне
- 12. Вариант пробного платного ЕГЭ На стороне CD квадрата ABCD построен равнобедренный прямоугольный треугольник CPD с гипотенузой
- 13. Решение Первый случай, когда точка Р лежит вне квадрата АВСD: 1. CD = 4, значит CP=PD=
- 14. Второй случай когда точка Р лежит внутри квадрата: Точка Р совпадет с точкой пересечения диагоналей, поэтому
- 15. Диагностическая работа от 20.10.10 Окружность S радиуса 12 вписана в прямоугольную трапецию с основаниями 28 и
- 16. Решение Первый случай, когда окружность касается нижнего основания: По свойству отрезков касательных, проведенных из одной точки
- 17. Второй случай, когда окружность касается верхнего основания. По теореме Пифагора найдем ОС = 15. Также используя
- 18. Диагностическая работа от 9.12.10 Расстояние между параллельными прямыми равно 12. на одной из них лежит точка
- 19. Решение Первый случай, когда С – вершина равнобедренного треугольника. По условию СН = 12, АС =
- 20. Второй случай, когда АС= АВ=13, СН=12 1. По теореме Пифагора АН=5, значит НВ=8, 2. Подставив в
- 21. Ященко и Со (30 вариантов-2011) В параллелограмме АВСD биссектрисы углов при стороне AD делят сторону ВС
- 22. Решение Первый случай, когда точки M и N лежат на отрезке ВС, считая от вершины В
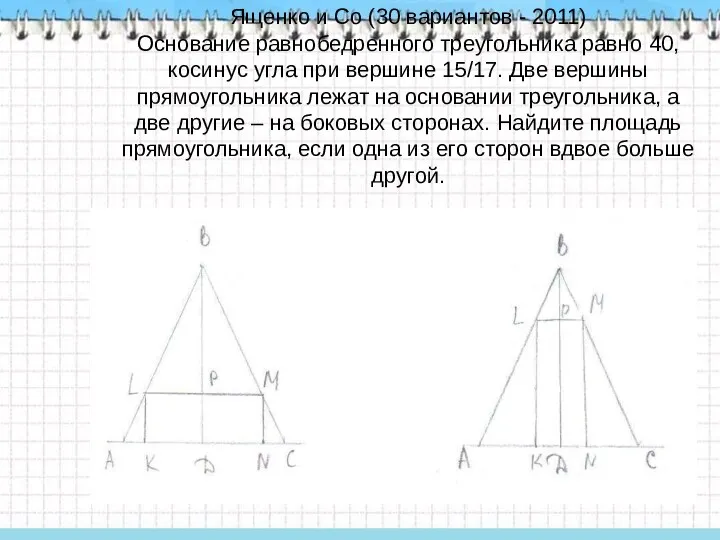
- 23. Ященко и Со (30 вариантов - 2011) Основание равнобедренного треугольника равно 40, косинус угла при вершине
- 24. Решение Первый случай, когда большая сторона прямоугольника лежит на основании. По теореме косинусов находим АВ =
- 25. Во втором случае на основании треугольника лежит меньшая сторона прямоугольника, тогда Пусть KN=x, KD=0,5x, LK=2x. Подставив
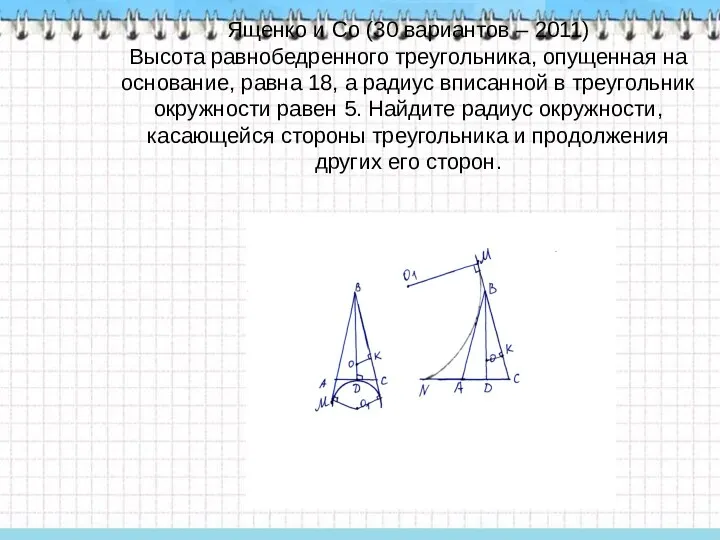
- 26. Ященко и Со (30 вариантов – 2011) Высота равнобедренного треугольника, опущенная на основание, равна 18, а
- 27. Решение Пусть ВС = a, АС = b, - радиус вневписанной окружности, касающейся стороны AC ,
- 28. 5. Применив свойство отрезка касательной к вневписанной окружности, получаем ВМ = 0,5 (19,5∙2+15)=27 6. Из формулы
- 29. Основные свойства и утверждения о взаимном расположении окружностей, о взаимном расположении прямой и окружности.
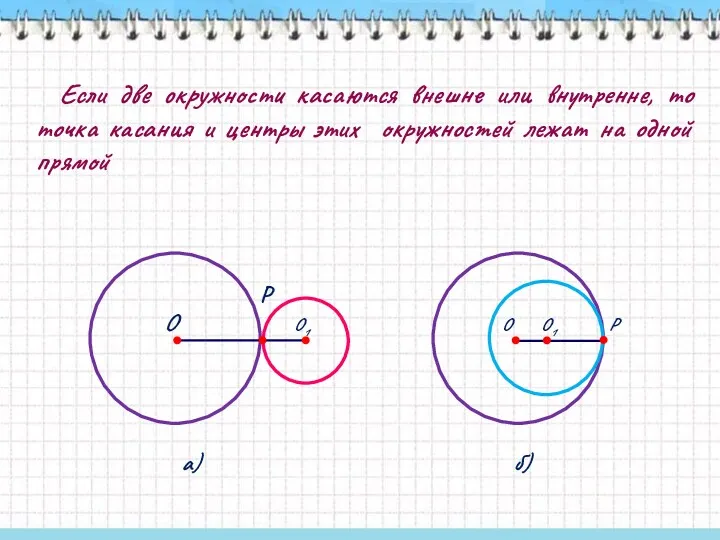
- 30. Если две окружности касаются внешне или внутренне, то точка касания и центры этих окружностей лежат на
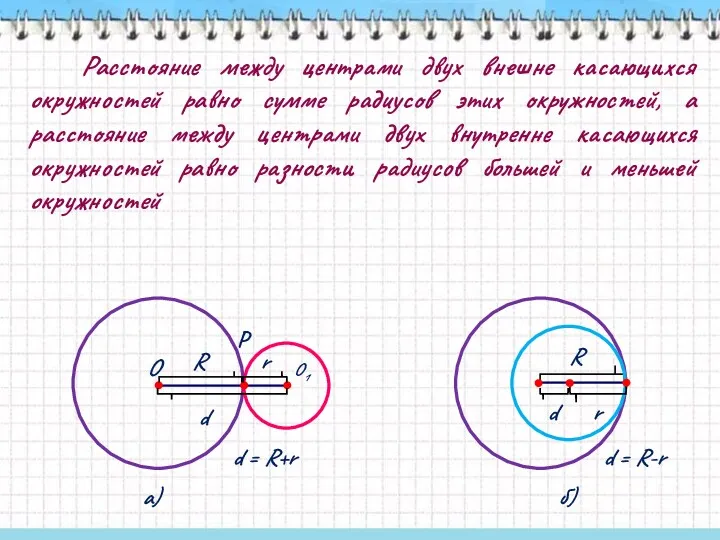
- 31. Расстояние между центрами двух внешне касающихся окружностей равно сумме радиусов этих окружностей, а расстояние между центрами
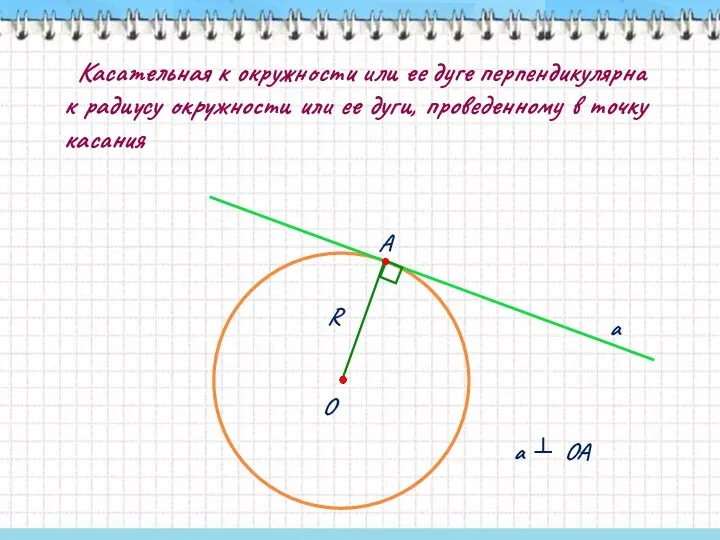
- 32. Касательная к окружности или ее дуге перпендикулярна к радиусу окружности или ее дуги, проведенному в точку
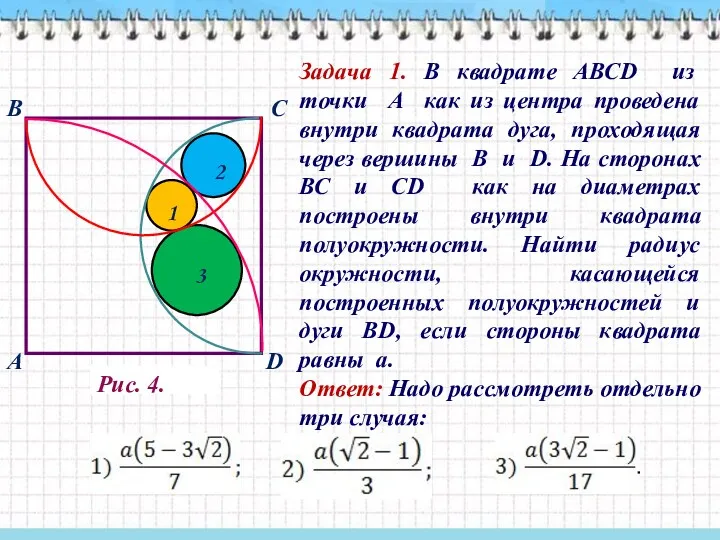
- 33. Задача 1. В квадрате АВСD, сторона которого равна а, из точки А как из центра проведена
- 34. Решение I. Случай, когда искомая окружность касается стороне АВ квадрата АВСD (Рис. 1, а). Обозначим радиус
- 35. Из прямоугольного треугольника АМО следует, что неизвестный катет АМ равен , то есть АМ= или АМ=
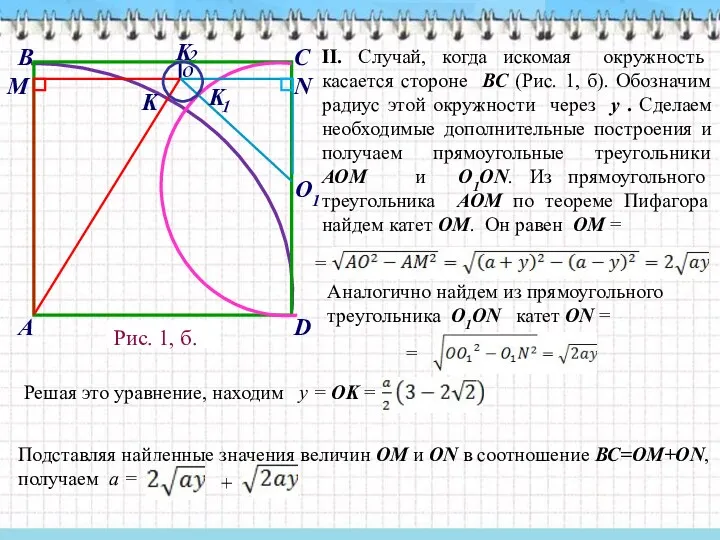
- 36. Рис. 1, б.
- 37. Рис. 1, в.
- 38. Задача 2 Дан круговой сектор АОВ радиуса R с центральным углом в 90 ○ . На
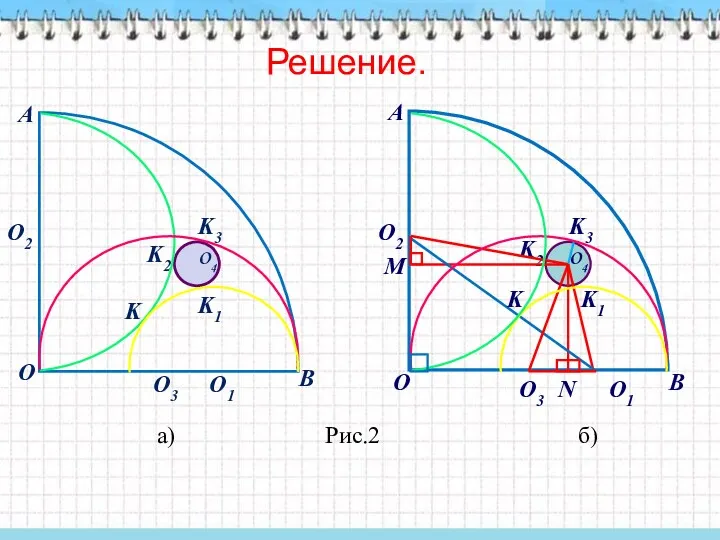
- 39. Решение. а) Рис.2 б) K1 O4 K3 K2 K2 K1 K3
- 40. Для решения этой задачи проведем из центров полуокружностей О1 и О2 радиусы в точки касания (Рис.2,б).
- 41. О1О42 - О3О42 = NО12 – NО32 , или (О1О4 - О3О4) (О1О4 +О3О4) = (NО1
- 42. Катет О2М = ОО2 - ОМ = и катет О4М = По теореме Пифагора имеем О2О4
- 43. Задача 3. На отрезке АВ, равном R, точка Q – середина; на АQ и на ВQ
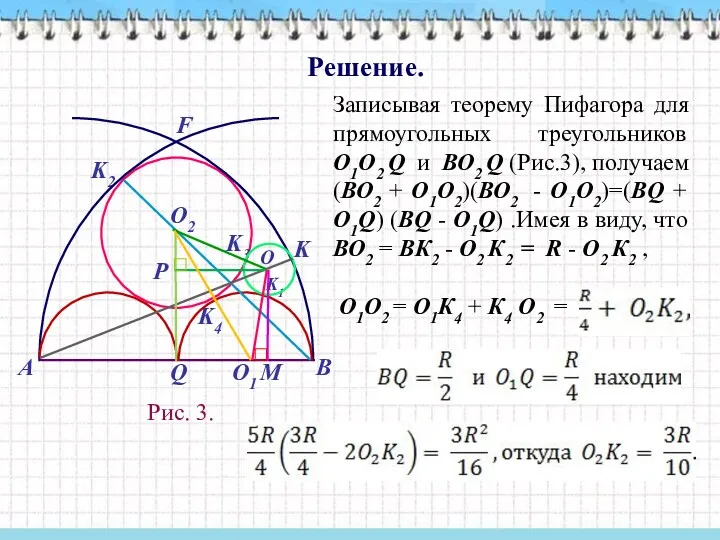
- 44. Решение. Рис. 3. Записывая теорему Пифагора для прямоугольных треугольников О1О2 Q и ВО2 Q (Рис.3), получаем
- 45. Далее, рассматривая прямоугольные треугольники О1ОМ и АОМ, имеем (АО + О1О) (АО - О1О) =( АМ
- 46. катет Отсюда получаем После необходимых преобразований находим искомый радиус
- 47. Задачи для самостоятельного решения
- 48. Рис. 4. Задача 1. В квадрате АВСD из точки А как из центра проведена внутри квадрата
- 49. Задача 2. Окружность вписана в квадрат со стороной 1. Из одной его вершины проведена дуга окружности
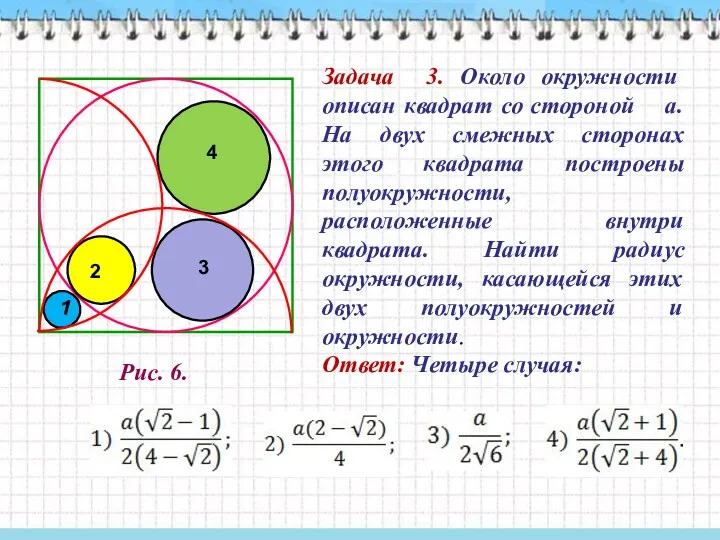
- 50. Задача 3. Около окружности описан квадрат со стороной а. На двух смежных сторонах этого квадрата построены
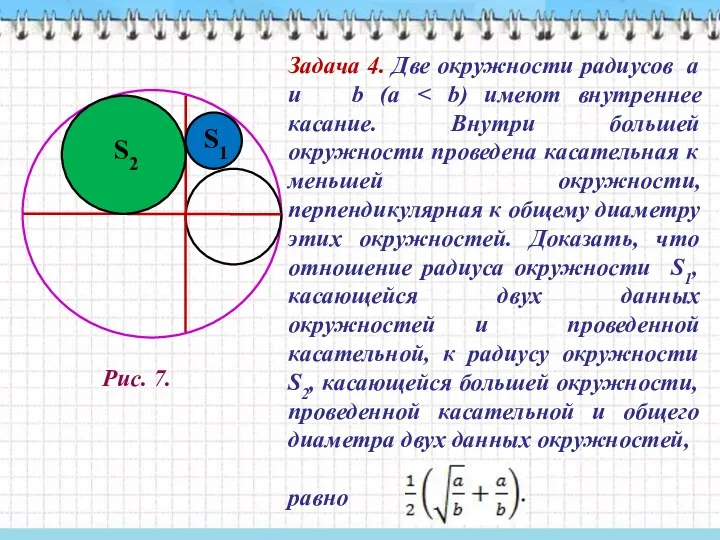
- 51. Задача 4. Две окружности радиусов a и b (a равно Рис. 7.
- 53. Скачать презентацию







































 Делимость суммы и разности чисел. Урок 102
Делимость суммы и разности чисел. Урок 102 Загальні відомості про дослідження операцій
Загальні відомості про дослідження операцій Точечные и интервальные оценки неизвестных параметров распределения
Точечные и интервальные оценки неизвестных параметров распределения Теория комплексных чисел. (Тема 2)
Теория комплексных чисел. (Тема 2) Неделя математики
Неделя математики Неопределенный интеграл
Неопределенный интеграл Истоки математики. Пифагор
Истоки математики. Пифагор Итоговый тест за курс начальной школы
Итоговый тест за курс начальной школы Принцип Дирихле
Принцип Дирихле Трапеція. Означення, властивості та види трапецій. Розв’язування задач. 8 класс
Трапеція. Означення, властивості та види трапецій. Розв’язування задач. 8 класс Презентация у уроку математики во 2 классе по теме Свойство противоположных сторон прямоугольника
Презентация у уроку математики во 2 классе по теме Свойство противоположных сторон прямоугольника Призма. Решение задач
Призма. Решение задач Первый признак равенства треугольников
Первый признак равенства треугольников Вероятность и статистика. Урок 2. 7 класс
Вероятность и статистика. Урок 2. 7 класс Математическая интерактивная игра Кем быть?.
Математическая интерактивная игра Кем быть?. Определённый интеграл. Вычисление площади криволинейной трапеции
Определённый интеграл. Вычисление площади криволинейной трапеции Правильная четырехугольная пирамида. Задачи
Правильная четырехугольная пирамида. Задачи Краткий запись задач 1 клас
Краткий запись задач 1 клас Общая теория. Графики. Тренажер
Общая теория. Графики. Тренажер Решение заданий В8 (часть 2) по материалам открытого банка задач ЕГЭ по математике
Решение заданий В8 (часть 2) по материалам открытого банка задач ЕГЭ по математике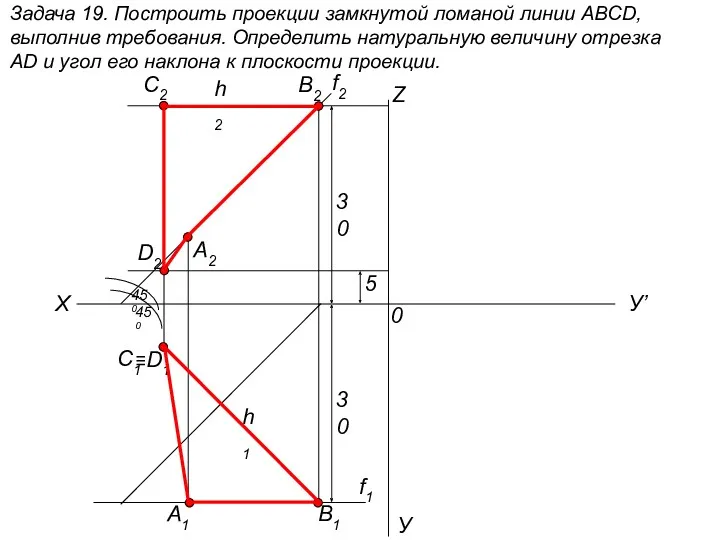 Построить проекции замкнутой ломаной линии ABCD, выполнив требования. (задача 19)
Построить проекции замкнутой ломаной линии ABCD, выполнив требования. (задача 19)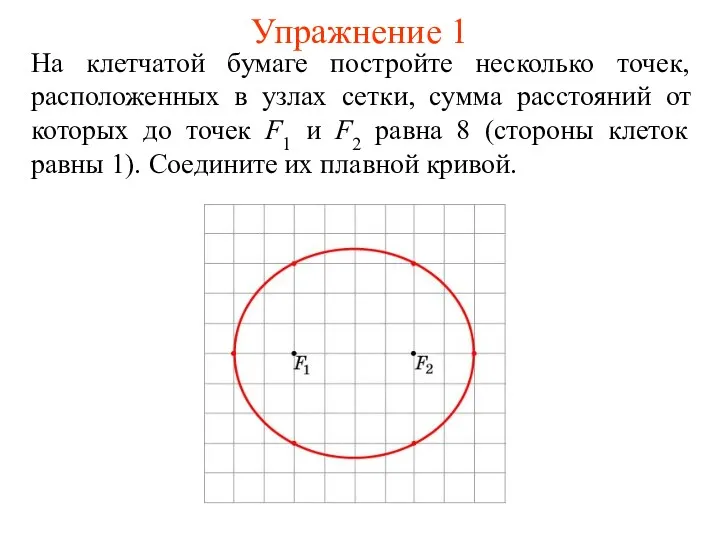 Эллипс
Эллипс Делители и кратные. 6 класс
Делители и кратные. 6 класс Арифметичні дії з іменованими числами математика
Арифметичні дії з іменованими числами математика Методическая разработка к уроку математики для 2 класса. Тема: Сложение однозначных чисел с переходом через разряд
Методическая разработка к уроку математики для 2 класса. Тема: Сложение однозначных чисел с переходом через разряд Сложение и умножение вероятностей
Сложение и умножение вероятностей Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Объем конуса
Объем конуса