Содержание
- 2. Натуральные числа Первоначальные представления о числе появились в эпоху каменного века. Древнему человеку было далеко до
- 3. Следующим пределом у славянского народа было число «тьма», (у древних греков - мириада), равное 10 000,
- 4. Архимед Зенон Элейский В Античном мире дальше всех продвинулись Архимед (III в. до н.э.) в «исчислении
- 5. 2 основные функции натуральных чисел: - характеристика количества предметов; - характеристика порядка предметов, размещенных в ряд.
- 6. Определение Натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого
- 7. Определение понятия: задачи в «натуральных числах» Г. А. Балл предлагает такое определение: «Задача в самом общем
- 8. А.П. Тонких дает следующее определение этому понятию «Текстовая задача - описание некоторой ситуации ( явления, процесса)
- 9. Различные модели решения задач в «натуральных числах» Решение математических текстовых задач. Основная особенность в решении математических
- 10. Решение: Поскольку полученная сумма, число «круглое», то, следовательно, количество купюр по 100 рублей кратно 1000. Таким
- 11. 2. Решение сюжетных задач, математической моделью которых является линейное диофантово уравнение. Ключевой идеей решения школьниками сюжетных
- 12. Решение: Математическая модель задачи – система двух линейных диофантовых уравнений: ? = 3? = 31, 34?
- 13. 3. Решение текстовых задач «на остатки». Ключевой идеей решения школьниками сюжетных задач «на остатки» является применение
- 14. Решение: Пусть первое число − x и второе − y. Не нарушая общности предположим что x
- 15. 4. Решение сюжетных задач на применение НОД и НОК. Ключевой идеей решения школьниками сюжетных задач применение
- 16. I способ. Наибольшее количество торговых точек, в которые можно поровну распределить 60 л подсолнечного и 48
- 17. II способ. Если бы подсолнечного масла было столько, сколько и кукурузного – 48 литров, то есть
- 18. 5. Решение задач «на стратегии». Ключевой идеей решения школьниками сюжетных задач теории игр – задач «на
- 19. I этап (экспериментальный). Я – Даша, моя цель – не дать Тане получить число делящееся на
- 20. II этап (логический). Даша начинает, а Таня – выигрывает, так как она заканчивает, а значит, может,
- 21. 6. Решение текстовых задач, математической моделью которых является алгебраическое уравнение или система уравнений. Математической моделью текстовой
- 23. Скачать презентацию




















 Оптимизация природопользования
Оптимизация природопользования Морское путешествие-2.Счет в пределах 20,вычитание 1 класс
Морское путешествие-2.Счет в пределах 20,вычитание 1 класс Прогрессия. Задачи с решениями
Прогрессия. Задачи с решениями Сложение отрицательных чисел
Сложение отрицательных чисел Урок математики в 1 классе по теме: Число и цифра 7 УМК Перспектива
Урок математики в 1 классе по теме: Число и цифра 7 УМК Перспектива Объемы тел. Решение задач
Объемы тел. Решение задач Тест Решение задач по теме Сложение и вычитание круглых сотен, 2 класс
Тест Решение задач по теме Сложение и вычитание круглых сотен, 2 класс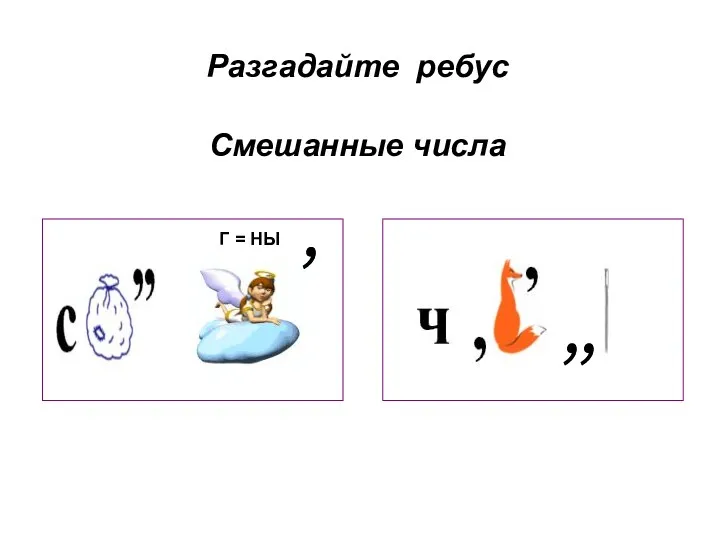 Смешанные числа. Ребус
Смешанные числа. Ребус Чтение графиков и диаграмм
Чтение графиков и диаграмм Счёт предметов.
Счёт предметов. презентация по математике на тему: Измеряем время
презентация по математике на тему: Измеряем время Деление обыкновенных дробей
Деление обыкновенных дробей Теорема о площади треугольника
Теорема о площади треугольника Луч, прямая, отрезок.
Луч, прямая, отрезок. Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости
Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости Radix sort
Radix sort Координатная плоскость. 7 класс
Координатная плоскость. 7 класс Повторення вивченого. Запис та складання виразів. Робота над задачами. Геометричний матеріал. Урок №66
Повторення вивченого. Запис та складання виразів. Робота над задачами. Геометричний матеріал. Урок №66 Подготовка к ЕГЭ. Площади фигур
Подготовка к ЕГЭ. Площади фигур Определение квадратичной функции
Определение квадратичной функции Сложение чисел с разными знаками
Сложение чисел с разными знаками Множества. Отношения между множествами
Множества. Отношения между множествами Степень с натуральным показателем и ее свойства
Степень с натуральным показателем и ее свойства Решение задач по теме Подобные слагаемые
Решение задач по теме Подобные слагаемые Число 7. Презентация к уроку математики в 1 классе.
Число 7. Презентация к уроку математики в 1 классе. Прямоугольный параллелепипед
Прямоугольный параллелепипед Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Число ноль
Число ноль