Содержание
- 2. – величине разброса СВ? Суть ЗБЧ заключается в следующем: при большом числе СВ Хi с вероятностью,
- 3. Смысл ЗБЧ в том, что разброс в воздействии отдельного явления мало сказывается на среднем результате большого
- 4. ЗБЧ включает: 1) Неравенство Чебышёва; 2) Лемму Маркова; 3) Обобщенную теорему Чебышёва; 4) Следствия из обобщенной
- 5. испытаний абсолютная величина отклонения СВ Х от ее математического ожидания не превзойдет положительного числа α >
- 6. Дано: p = 0,9 q = 0,1 n = 4000 M(X) – α = 3550 M(X)
- 7. Лемма Маркова Пусть СВ Х принимает положительные значения. Лемма Маркова. С вероятностью, большей чем , можно
- 8. P( X ≤ a ) > 1 - Задача. Вероятность попадания в цель равна 0.4. Оценить
- 9. Обобщенная теорема Чебышёва Теорема. Если дисперсии независимых СВ Xi ограничены сверху числом С = const, то
- 10. Σ M(Xi) - среднее арифметическое их математических ожиданий. Если n – число СВ, а их дисперсии
- 11. всех размеров деталей ≤ 9. Оценить вероятность того, что средний размер деталей проверенной партии отличается от
- 12. Следствия из обобщенной теоремы Чебышёва а) Теорема Бернулли Теорема. При бесконечно большом числе незави-симых испытаний с
- 13. Если n – число независимых испытаний, а p – вероятность события А в каждом испытании, то
- 14. Дано: n = 10000 p = 0,75 q = 0,25 P(│m – m0│≤ 100) >? │m
- 15. б) Теорема Пуассона При неограниченном увеличении числа независи- мых испытаний с вероятностью pi появления события А
- 16. Оценочное неравенство теоремы Пуассона: P(│ - p│≤ ε ) >1 - , где pq = -
- 17. 2-го – 0,8. Оценить вероятность того, что относи- тельная частота бракованной детали отличается от средней вероятности
- 18. Закон больших чисел Теорема. При неограниченном увеличении числа независимых испытаний n над СВ Х, имею- щей
- 19. Если D(X) ≤ C, то P(│ М(Х)│≤ ε ) > 1 - Задача. Для определения среднего
- 21. Скачать презентацию




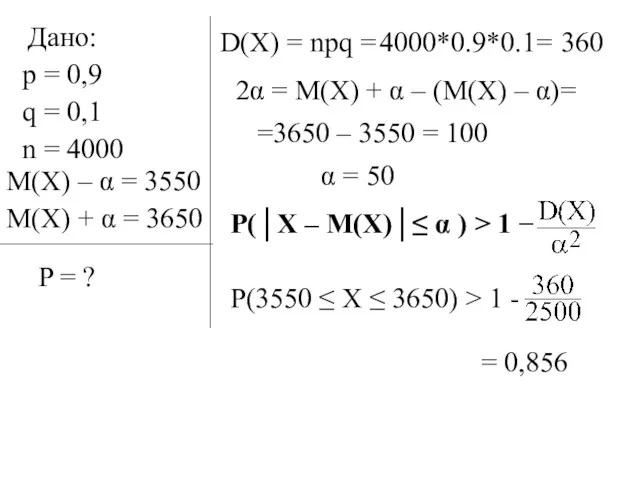







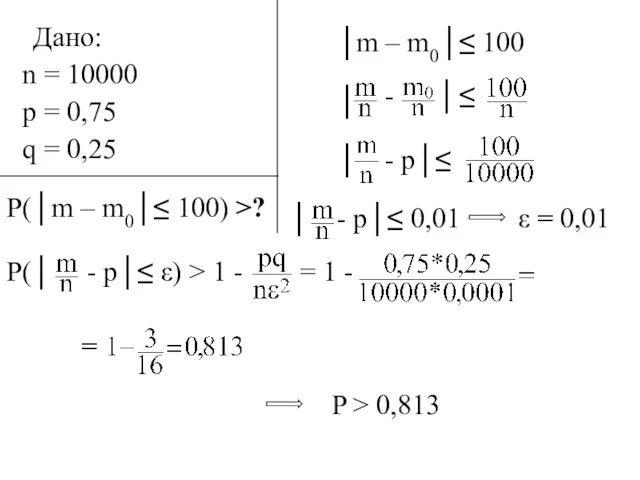





 Открытый урок по математике в 3-м классе Единица времени - сутки
Открытый урок по математике в 3-м классе Единица времени - сутки Диференціальні рівняння другого порядку
Диференціальні рівняння другого порядку Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Шартты операция
Шартты операция Презентация: Логические задачи в курсе математики начальной школы
Презентация: Логические задачи в курсе математики начальной школы Сфера и шар
Сфера и шар Закрепление пройденного материала
Закрепление пройденного материала Математический турнир для начальных классов
Математический турнир для начальных классов Точка. Кривая линия. Прямая линия. Отрезок. Луч
Точка. Кривая линия. Прямая линия. Отрезок. Луч Математика. 1 класс. Урок 55. Числа 0-10 - Презентация
Математика. 1 класс. Урок 55. Числа 0-10 - Презентация Правильные и неправильные дроби
Правильные и неправильные дроби Случаи вычитания 17 -, 18 -
Случаи вычитания 17 -, 18 - урок по математике
урок по математике Презентация к уроку Приёмы письменного умножения трёхзначных чисел на однозначные.
Презентация к уроку Приёмы письменного умножения трёхзначных чисел на однозначные. Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3)
Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3) Интерактивный тренажёр. В гости к Смешарикам Таблица умножения и деления на 9.
Интерактивный тренажёр. В гости к Смешарикам Таблица умножения и деления на 9. Формулы сокращенного умножения
Формулы сокращенного умножения Квадратичная функция. Ее свойства и график
Квадратичная функция. Ее свойства и график Письменное деление на двузначное число. Закрепление
Письменное деление на двузначное число. Закрепление Урок геометрии в 8 классе по теме Параллелограмм
Урок геометрии в 8 классе по теме Параллелограмм Случайная изменчивость
Случайная изменчивость Розв'язування показникових нерівностей
Розв'язування показникових нерівностей Тест по геометрии, часть А
Тест по геометрии, часть А Числитель и знаменатель дробей
Числитель и знаменатель дробей Линейная функция и ее график. 7 класс
Линейная функция и ее график. 7 класс Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Parallelogram
Parallelogram Предел функции на бесконечности
Предел функции на бесконечности