Содержание
- 2. Ключевые слова алгебра логики высказывание логическая операция конъюнкция дизъюнкция отрицание логическое выражение таблица истинности законы логики
- 3. Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике Логика Аристотель (384-322 до
- 4. Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими
- 5. Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
- 6. Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний. В алгебре логики высказывания обозначают
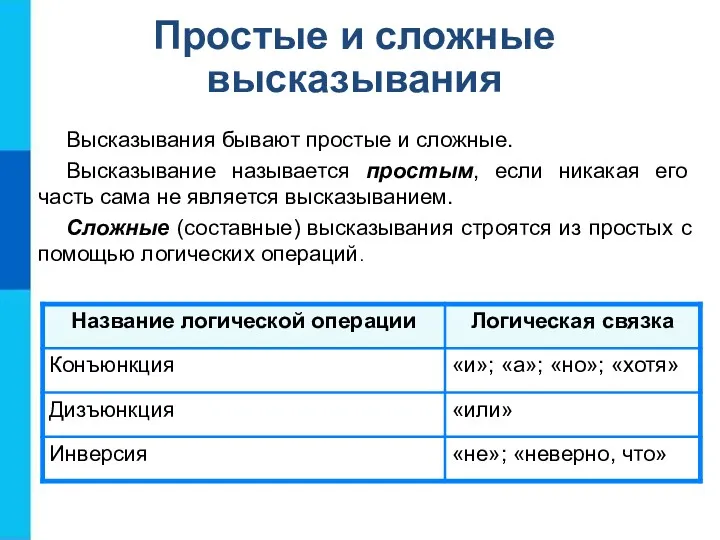
- 7. Простые и сложные высказывания Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть
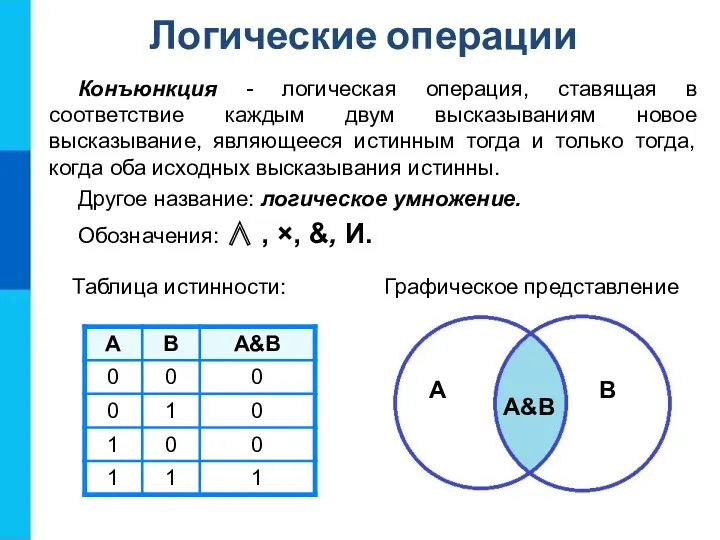
- 8. Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и
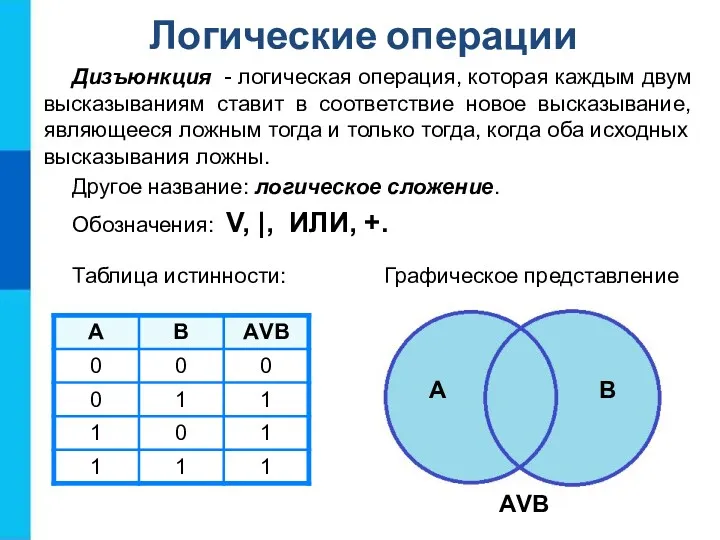
- 9. Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда
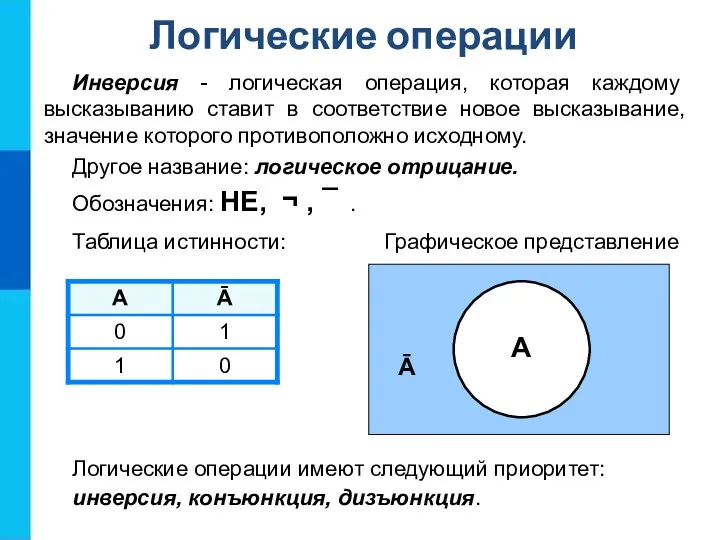
- 10. Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
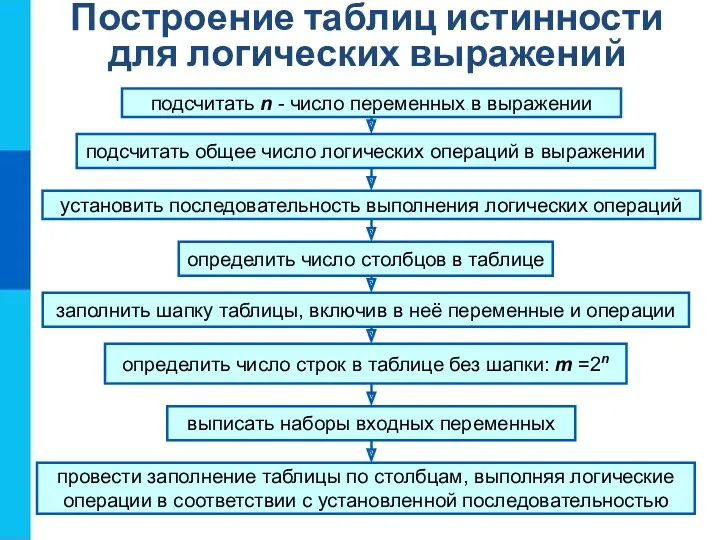
- 11. Построение таблиц истинности для логических выражений подсчитать n - число переменных в выражении подсчитать общее число
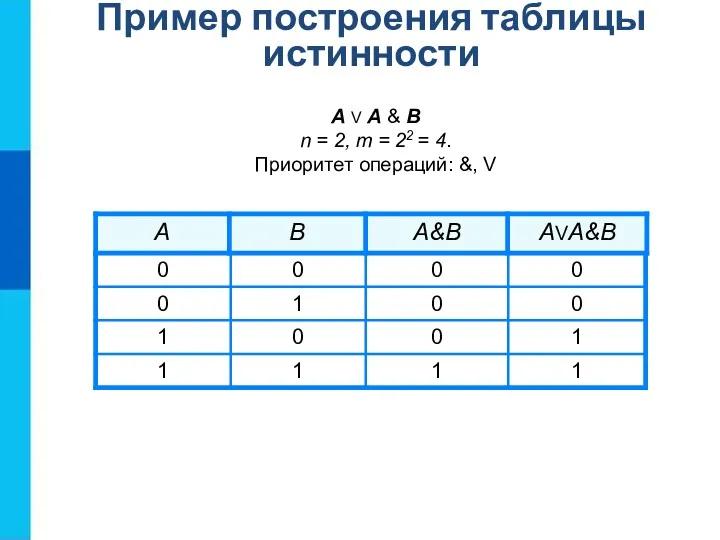
- 12. А V A & B n = 2, m = 22 = 4. Приоритет операций: &,
- 13. Задача. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую
- 14. Решение. Пусть К =«Коля разбил вазу», В =«Вася разбил вазу», С =«Серёжа разбил вазу». Представим в
- 15. Вопросы и задания Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и
- 17. Скачать презентацию








 Иллюстрированные правила игры. Twilight imperium 3rd edition
Иллюстрированные правила игры. Twilight imperium 3rd edition Методика проведения юзабилити-тестирования веб-сайта
Методика проведения юзабилити-тестирования веб-сайта Ресурсы для организации дистанционного обучения (1)
Ресурсы для организации дистанционного обучения (1) Необобщенные коллекции
Необобщенные коллекции Разработка программных модулей. Графические построения. Контурные фигуры
Разработка программных модулей. Графические построения. Контурные фигуры Учебные курсы по Microsoft® Office Word 2007
Учебные курсы по Microsoft® Office Word 2007 Разработка модели и решение задачи управления запасами на примере компании К-спойлер
Разработка модели и решение задачи управления запасами на примере компании К-спойлер Что такое Unity и Vuforia
Что такое Unity и Vuforia Абстрактные классы и интерфейсы. (Занятие 4)
Абстрактные классы и интерфейсы. (Занятие 4) Questio n6. Answer
Questio n6. Answer Нечеткая нейронная сеть
Нечеткая нейронная сеть Қазіргі заманғы жоғары дәрежелі Delphi тілі
Қазіргі заманғы жоғары дәрежелі Delphi тілі Анализ алгоритмов решения математических задач (Работа с числами разных форматов)
Анализ алгоритмов решения математических задач (Работа с числами разных форматов) Развитие вычислительной техники и архитектура
Развитие вычислительной техники и архитектура Программирование (Python). § 17. Введение
Программирование (Python). § 17. Введение هيكلية الحاسوب
هيكلية الحاسوب Разработка системы управления сайтом туристического агентства
Разработка системы управления сайтом туристического агентства Всемирная паутина Логический поиск информации в сети интернет
Всемирная паутина Логический поиск информации в сети интернет Разработка системы обмена мгновенными сообщениями на JAVA
Разработка системы обмена мгновенными сообщениями на JAVA Понятие алгоритма. Исполнители алгоритмов. Виды алгоритмов
Понятие алгоритма. Исполнители алгоритмов. Виды алгоритмов Introduction to JavaScript Functions (part 3)
Introduction to JavaScript Functions (part 3) Как работать в системе АИС Путевка
Как работать в системе АИС Путевка Интернет вещей
Интернет вещей Задачи
Задачи Платформы Web of Science и Scopus: базовые возможности
Платформы Web of Science и Scopus: базовые возможности Комплексный подход к защите информации. (Лекция 3)
Комплексный подход к защите информации. (Лекция 3) Формализациялау жөніндетүсінік, инфармацияны формализациялаудың негізгі тұрлері: формула, мәтін, кесте граф, алгоритм
Формализациялау жөніндетүсінік, инфармацияны формализациялаудың негізгі тұрлері: формула, мәтін, кесте граф, алгоритм Знакомство с minecraft. Занятие 1
Знакомство с minecraft. Занятие 1