Содержание
- 2. Цель лекции – изучение основных понятий теории множеств, способов задания множеств, законов алгебры множеств Содержание: Курс
- 3. Литература Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986. C. 4-8. Лавров И.А., Максимова Л.Л.
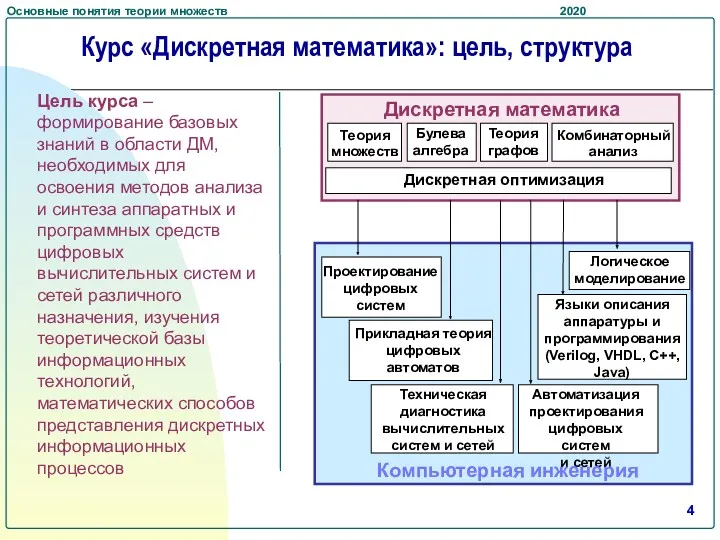
- 4. Курс «Дискретная математика»: цель, структура Цель курса – формирование базовых знаний в области ДМ, необходимых для
- 5. Курс «Дискретная математика»: знания, умения, навыки
- 6. Немецкий ученый, математик, создатель теории множеств Родился в Петербурге в 1845г. В 1867 г. окончил Берлинский
- 7. Сегодня мы знаем, что, логически говоря, возможно вывести почти всю современную математику из единого источника –
- 8. Термины Ключевые слова: подмножество принадлежность включение мощность пустое множество универсум булеан объединение пересечение дополнение симметрическая разность
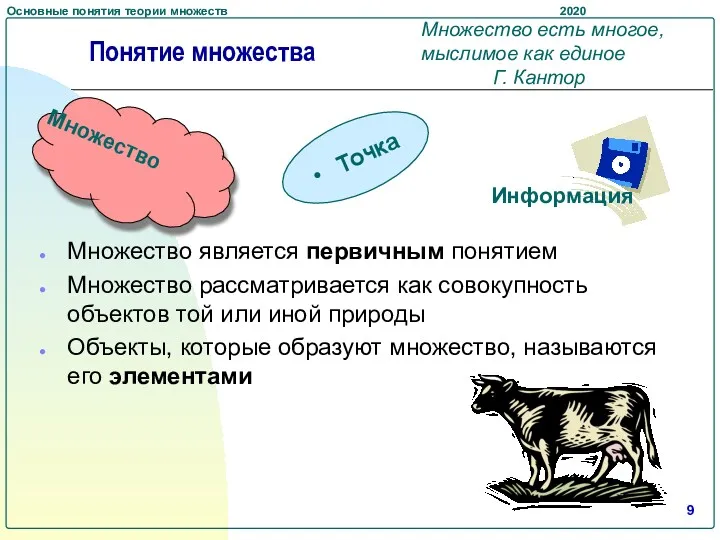
- 9. Множество является первичным понятием Множество рассматривается как совокупность объектов той или иной природы Объекты, которые образуют
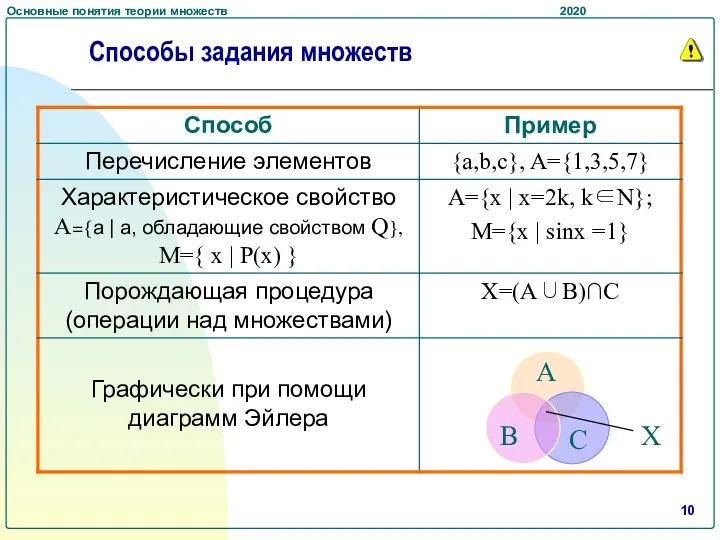
- 10. Способы задания множеств
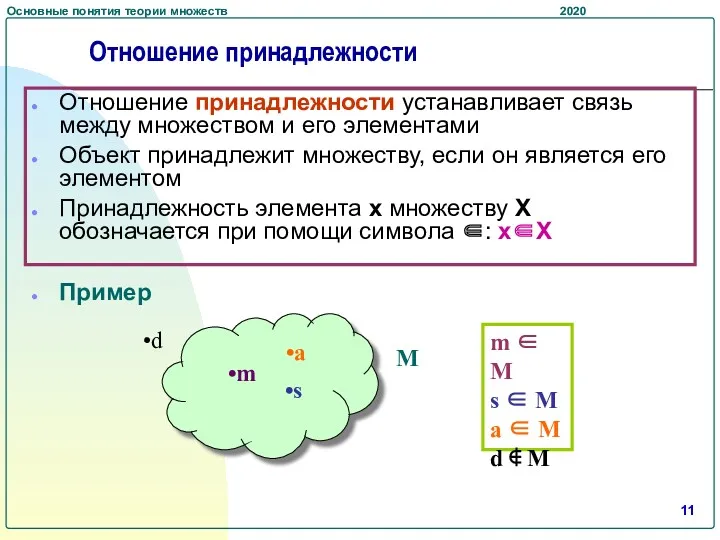
- 11. Отношение принадлежности устанавливает связь между множеством и его элементами Объект принадлежит множеству, если он является его
- 12. Отношение включения Устанавливает связь между двумя множествами: (A ⊆B) ⇔ (∀m∈A ⇒ m∈B) Обозначение: ⊂ –
- 13. Отношения принадлежности и включения: пример Дано множество A= {1, 2, 3, {3}, {4} }. Какие из
- 14. Time Out
- 15. Мощность множества. Пустое и универсальное множества Мощность множества или кардинальное число определяет количество элементов данного множества
- 16. Булеан – множество всех подмножеств данного множества M Обозначение: B(M) Пример: дано множество A={a, b, c}.
- 17. Операции над множествами А В A B A A A B
- 18. Законы и тождества алгебры множеств Кантора. 1
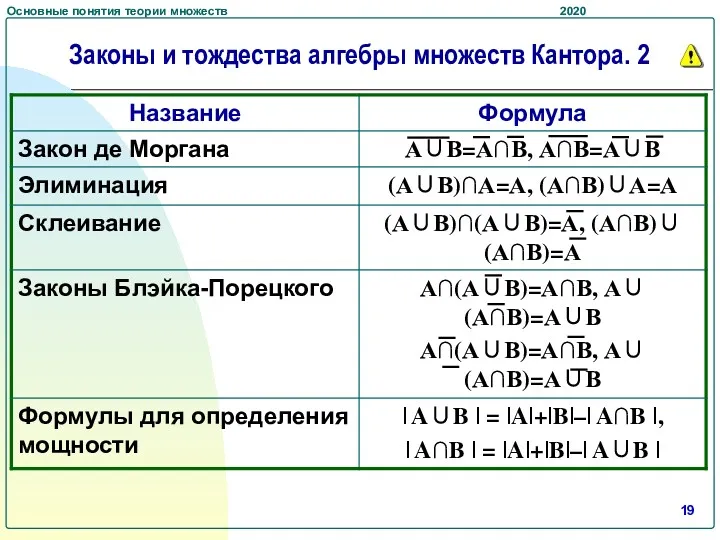
- 19. Законы и тождества алгебры множеств Кантора. 2
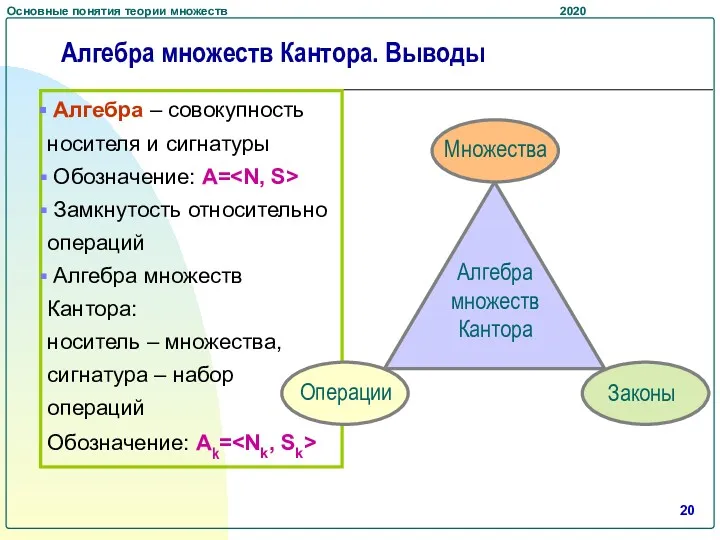
- 20. Алгебра множеств Кантора. Выводы Алгебра – совокупность носителя и сигнатуры Обозначение: А= Замкнутость относительно операций Алгебра
- 21. Тест-вопросы 1. Могут ли повторяться элементы множества? а) да; б) нет. 2. Является ли множество несобственным
- 23. Скачать презентацию














 Порівняння раціональних чисел. Математика. 6 клас
Порівняння раціональних чисел. Математика. 6 клас Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми Урок математики Решение задач
Урок математики Решение задач урок математики
урок математики Точечные перфокарты.
Точечные перфокарты. Итоговый тест по математике
Итоговый тест по математике Числовые последовательности
Числовые последовательности Уравнение окружности (9 класс)
Уравнение окружности (9 класс) Практическое применение знаний по математике, связанных с сельским хозяйством
Практическое применение знаний по математике, связанных с сельским хозяйством Урок математики в 1 классе на тему Приёмы сложения и вычитания, основанные на знании нумерации чисел
Урок математики в 1 классе на тему Приёмы сложения и вычитания, основанные на знании нумерации чисел Круглые числа. Состав числа 9. Сравнение выражений
Круглые числа. Состав числа 9. Сравнение выражений Урок Числа от 10 до 20
Урок Числа от 10 до 20 Вычитание чисел (часть 1)
Вычитание чисел (часть 1) Применение признаков равенства треугольников при решении задач
Применение признаков равенства треугольников при решении задач Метод максимального правдоподобия
Метод максимального правдоподобия Формирование УУД на различных этапах урока математики по ТДМ.
Формирование УУД на различных этапах урока математики по ТДМ. Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Дифференциальные уравнения и их применение в медицинской практике
Дифференциальные уравнения и их применение в медицинской практике Второй признак равенства треугольников
Второй признак равенства треугольников Элементы матанализа. Применение производной при исследовании функции
Элементы матанализа. Применение производной при исследовании функции Таблица деления на 3
Таблица деления на 3 Функция её свойства и график
Функция её свойства и график Ряды динамики. Статистика
Ряды динамики. Статистика Vienkāršās formas
Vienkāršās formas Математический КВН
Математический КВН Вписані і центральні кути
Вписані і центральні кути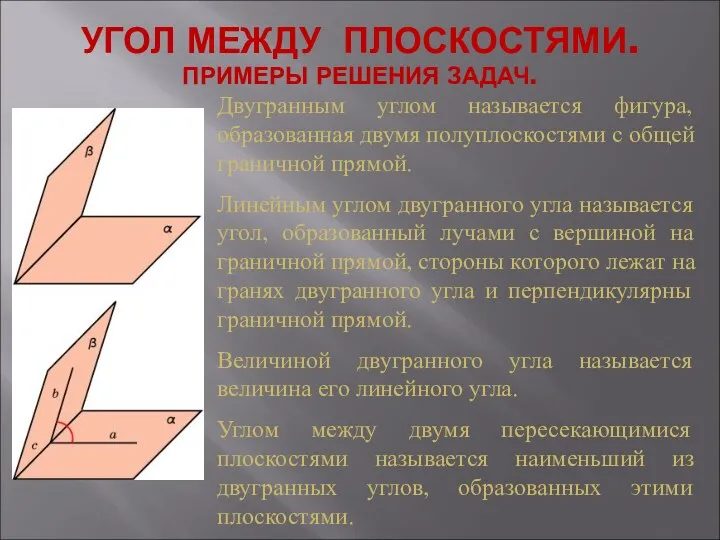 Угол между плоскостями. Примеры решения задач
Угол между плоскостями. Примеры решения задач Высота и скорость полета. (Тема 6)
Высота и скорость полета. (Тема 6)