Содержание
- 2. Содержание. Введение Цель работы Что такое граф История возникновения графов Задача о Кенигсбергских мостах Одним росчерком
- 3. Цель работы. Изучить определение и свойства графа. Исследовать роль графов в нашей жизни. Научиться применять теорию
- 4. История возникновения графов. Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая
- 5. Задача о кёнигсбергских мостах. (Задача о кёнингсбергских мостах). Бывший Кёнигсберг (ныне Калининград) расположен на реке Прегель
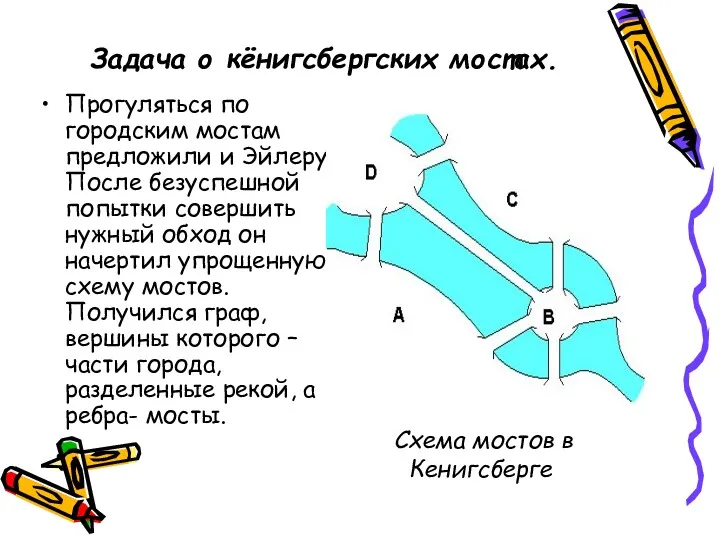
- 6. Задача о кёнигсбергских мостах. Прогуляться по городским мостам предложили и Эйлеру. После безуспешной попытки совершить нужный
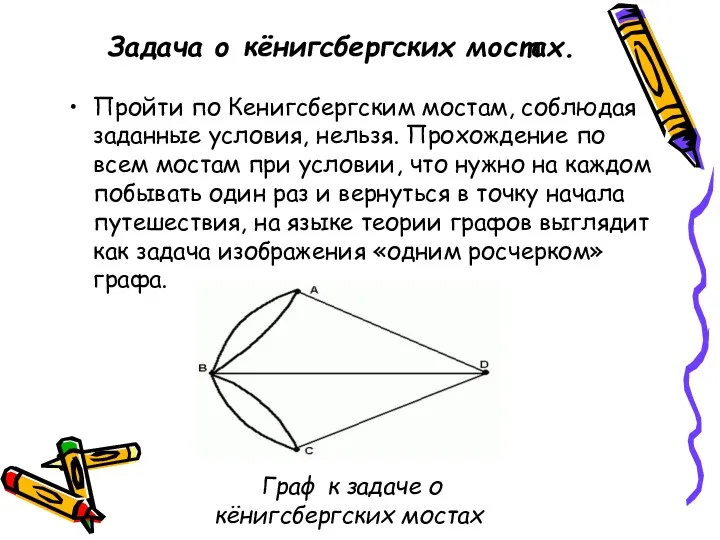
- 7. Задача о кёнигсбергских мостах. Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам
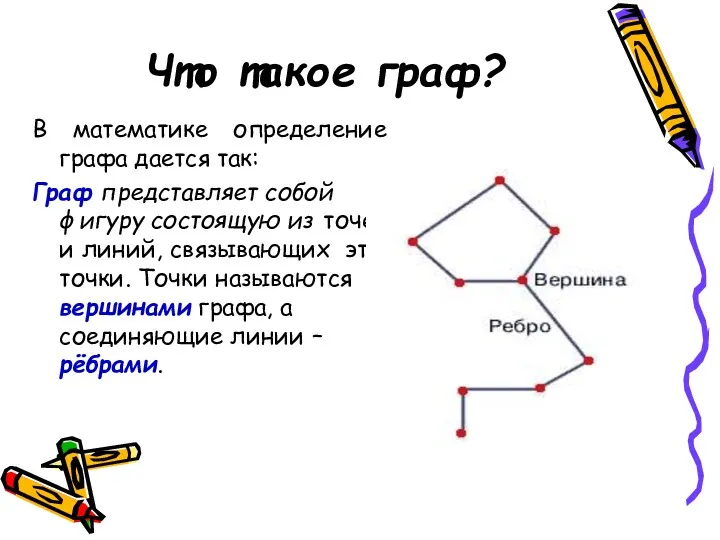
- 8. Что такое граф? В математике определение графа дается так: Граф представляет собой фигуру состоящую из точек
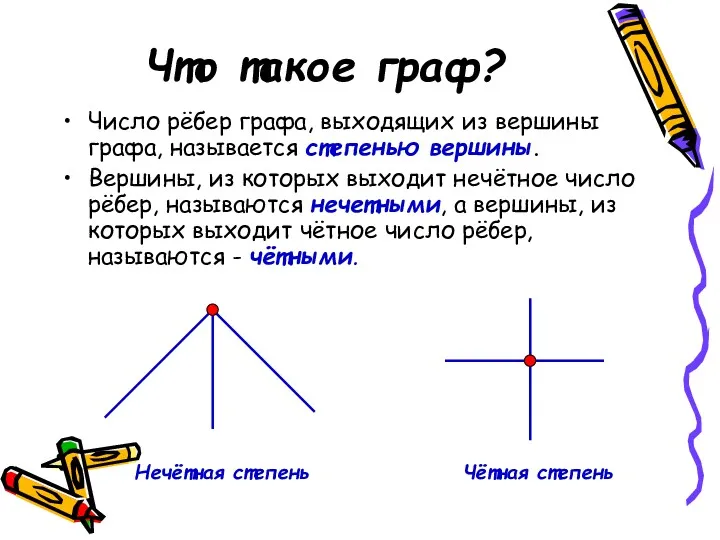
- 9. Что такое граф? Число рёбер графа, выходящих из вершины графа, называется степенью вершины. Вершины, из которых
- 10. Вывод к задаче о Кенингсбергских мостах: В задаче о кенигсбергских мостах все четыре вершины соответствующего графа
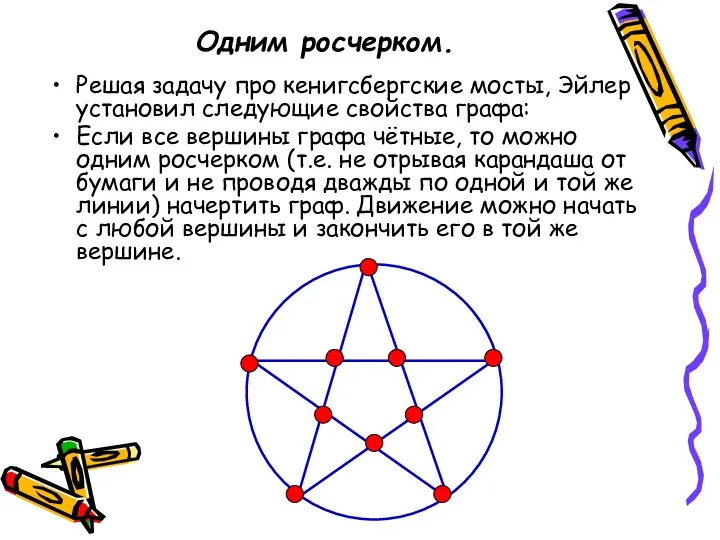
- 11. Одним росчерком. Решая задачу про кенигсбергские мосты, Эйлер установил следующие свойства графа: Если все вершины графа
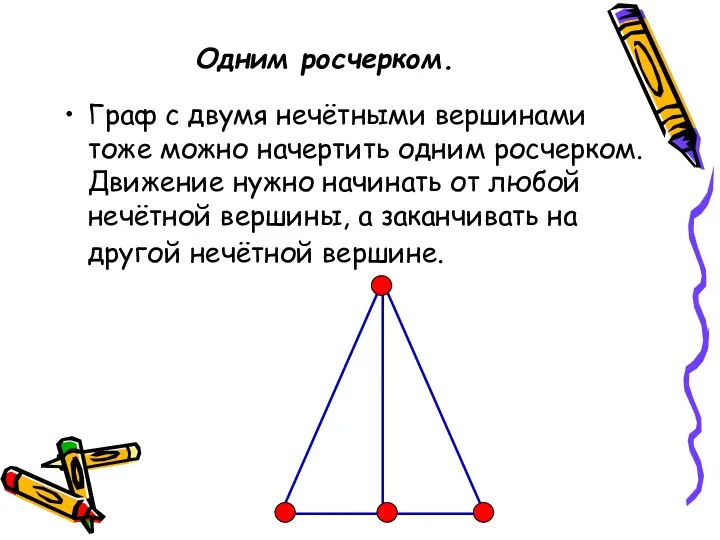
- 12. Одним росчерком. Граф с двумя нечётными вершинами тоже можно начертить одним росчерком. Движение нужно начинать от
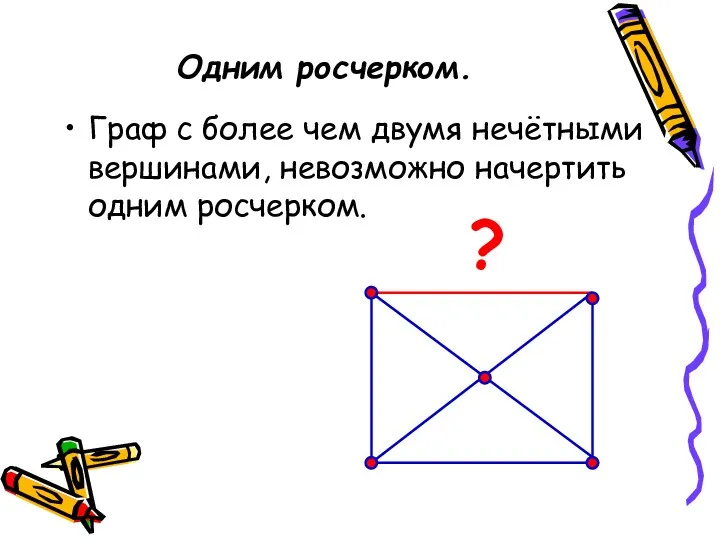
- 13. Одним росчерком. Граф с более чем двумя нечётными вершинами, невозможно начертить одним росчерком. ?
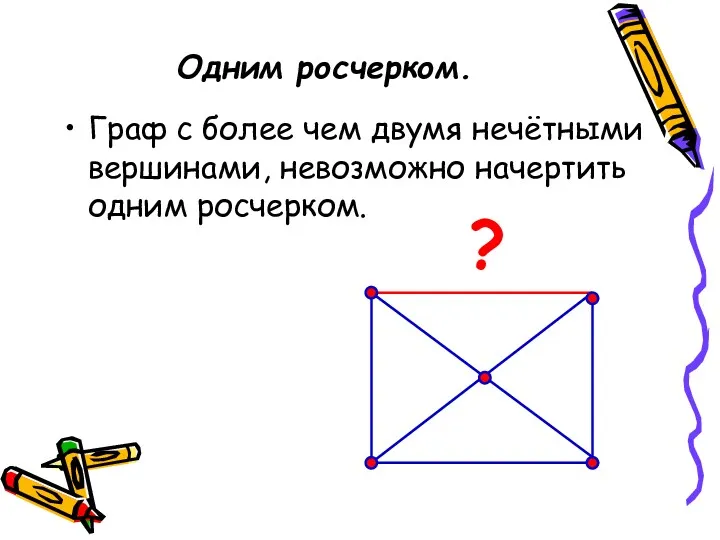
- 14. Одним росчерком. Граф с более чем двумя нечётными вершинами, невозможно начертить одним росчерком. ?
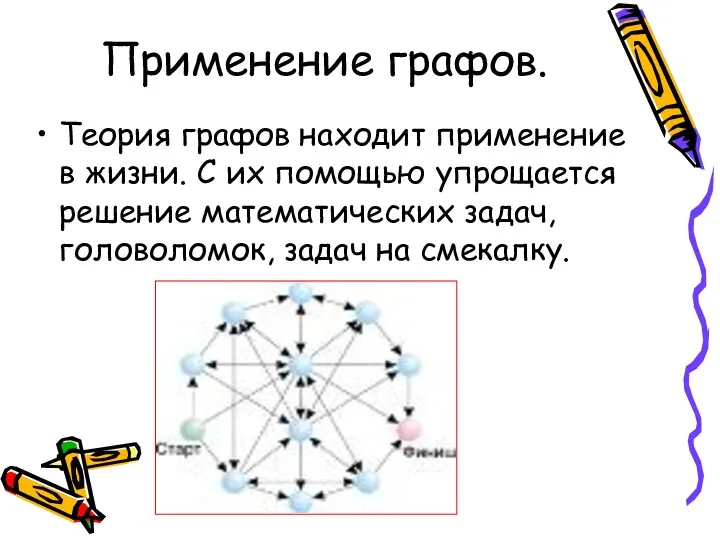
- 15. Применение графов. Теория графов находит применение в жизни. С их помощью упрощается решение математических задач, головоломок,
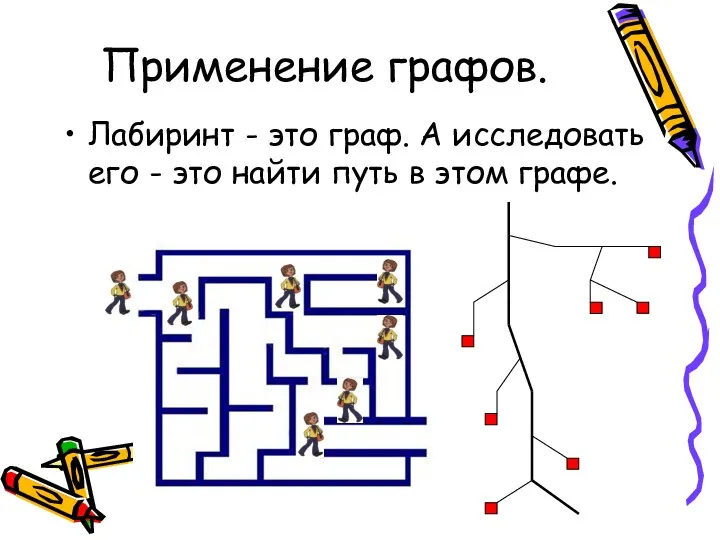
- 16. Применение графов. Лабиринт - это граф. А исследовать его - это найти путь в этом графе.
- 17. Применение графов. Типичными графами на географических картах изображения железных дорог.
- 18. Применение графов. Графы есть и на картах звездного неба.
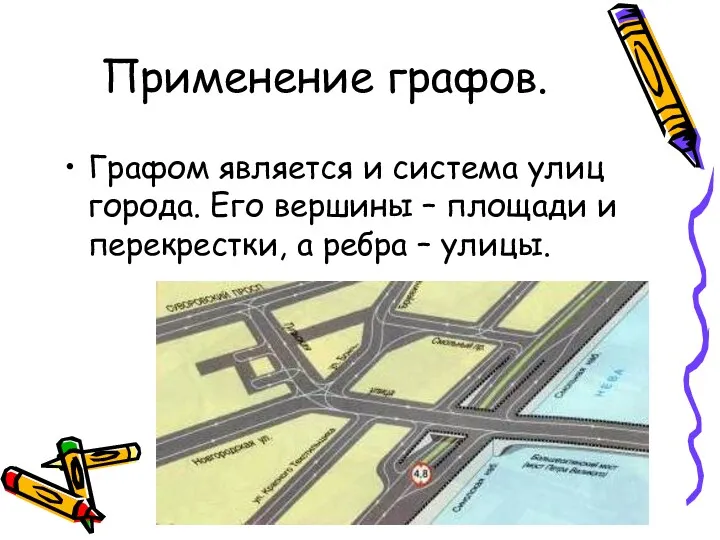
- 19. Применение графов. Графом является и система улиц города. Его вершины – площади и перекрестки, а ребра
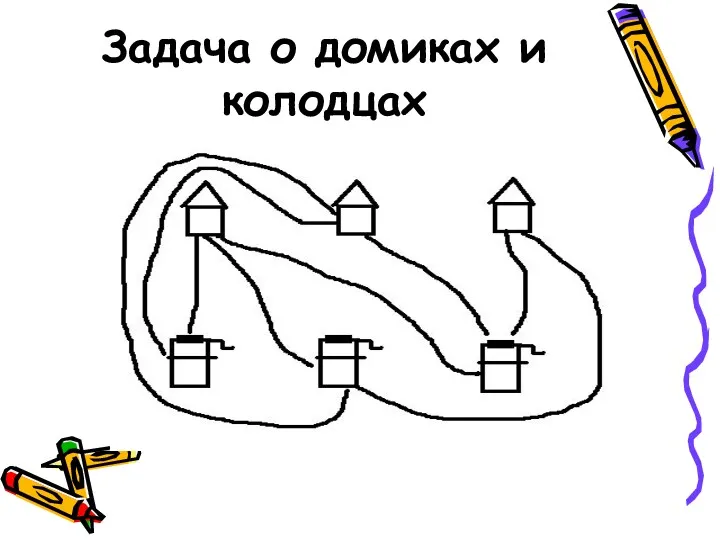
- 20. Задача о домиках и колодцах В некоторой деревне есть три колодца. Трое жителей, живущие в трех
- 21. Задача о домиках и колодцах
- 22. Выводы. Графы – это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические
- 24. Скачать презентацию









 Объём. Решение задач с практическим содержанием
Объём. Решение задач с практическим содержанием Пифагор и теорема Пифагора
Пифагор и теорема Пифагора Тест. Задания В1, ЕГЭ по математике
Тест. Задания В1, ЕГЭ по математике Деление десятичных дробей
Деление десятичных дробей Моделирование объекта принятия решений на основе проверки многомерных статистических гипотез
Моделирование объекта принятия решений на основе проверки многомерных статистических гипотез Урок 12. Числовые характеристики распределения дискретных и непрерывных случайных величин
Урок 12. Числовые характеристики распределения дискретных и непрерывных случайных величин Исследовательская работа. Рациональные методы устных вычислений
Исследовательская работа. Рациональные методы устных вычислений периметр
периметр Статистические характеристики
Статистические характеристики Сложение и вычитание в пределах 20.
Сложение и вычитание в пределах 20. Елементи диференційного числення функції однієї та багатьох змінних. Інтегральне числення. Диференційні рівняння. Лекція 1
Елементи диференційного числення функції однієї та багатьох змінних. Інтегральне числення. Диференційні рівняння. Лекція 1 Цена, количество, стоимость. Решение задач
Цена, количество, стоимость. Решение задач Многоугольник. Внутренняя область
Многоугольник. Внутренняя область Космические спасатели спешат на помощь
Космические спасатели спешат на помощь Математика и космос
Математика и космос Организация исследовательской деятельности обучающихся на уроках математики
Организация исследовательской деятельности обучающихся на уроках математики Симметрия в английской символике. Бинарный урок
Симметрия в английской символике. Бинарный урок Устные задачи на готовых чертежах. Смежные и вертикальные углы
Устные задачи на готовых чертежах. Смежные и вертикальные углы Презентация Блоки Дьенеша
Презентация Блоки Дьенеша Математические методы моделирования и прогнозирования экономических процессов
Математические методы моделирования и прогнозирования экономических процессов Деление на однозначное число в столбик. Повторение
Деление на однозначное число в столбик. Повторение Письменное умножение на двузначное число
Письменное умножение на двузначное число Замечательные кривые
Замечательные кривые Презентация к уроку математики 1 класс
Презентация к уроку математики 1 класс Алгебраические дроби
Алгебраические дроби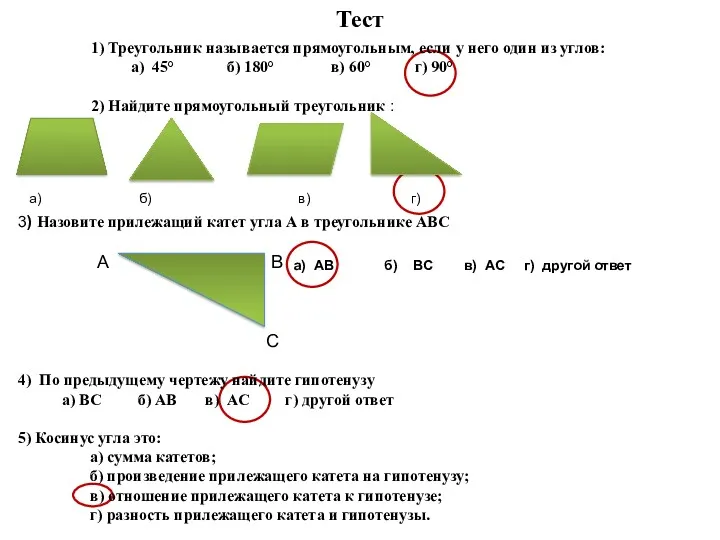 Тест. Прямоугольный треугольник
Тест. Прямоугольный треугольник Развитие познавательных способностей через игры математической направленности Опыт работы воспитателя ГБДОУ №68 Калининского района Остроуховой Натальи Васильевны Диск
Развитие познавательных способностей через игры математической направленности Опыт работы воспитателя ГБДОУ №68 Калининского района Остроуховой Натальи Васильевны Диск презентация задачи в стихах (два действия)
презентация задачи в стихах (два действия)