Содержание
- 2. УЧЕБНЫЕ ВОПРОСЫ 3. Общая схема применения определенного интеграла к решению геометрических и физических задач.( ознакомительно) 4.
- 3. ЛИТЕРАТУРА [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004. с. 340-375; [3]
- 4. УЧЕБНЫЙ ВОПРОС. Общая схема применения определенного интеграла к решению геометрических и физических задач.
- 5. Общая схема применения определенного интеграла к решению геометрических и физических задач. Пусть требуется найти значение какой-либо
- 6. 2) метод дифференциала, сущность которого заключается в том, что сначала составляется дифференциал искомой величины, а затем
- 7. Пример. Пусть материальная точка М перемещается вдоль оси Ox под действие силы F=F(x). Найдем работу A
- 8. Приближенное значение работы на [a;b] есть Это приближенное равенство тем точнее, чем меньше длина , поэтому
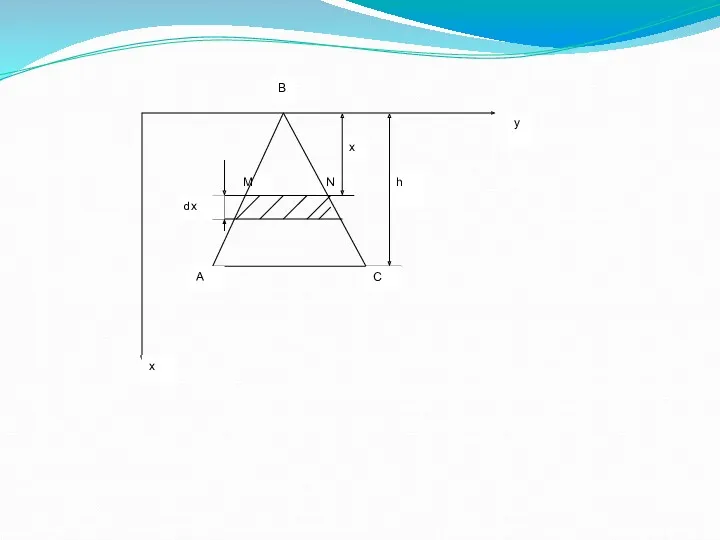
- 9. Пример. Вычислить силу давления воды на вертикальную площадку, имеющую форму треугольника с основанием 5 м и
- 11. Рассмотрим горизонтальную полоску толщиной dx, находящуюся на глубине х . Принимая эту полоску за прямоугольник, находим
- 12. УЧЕБНЫЙ ВОПРОС Вычисление площадей плоских фигур и длин дуг плоских линий в декартовых и полярных координатах.
- 13. Вычисление площадей плоских фигур в декартовых координатах. Если непрерывная функция f(x)≥0 на [a;b], то площадь S
- 14. Пусть на [a;b] заданы непрерывные функции y=f1(x) и y=f2(x) такие, что f2(x)≥ f1(x). Тогда площадь S
- 15. Пример. Найти площадь фигуры, ограниченной линиями y=x2-2, y=x. Решение. Для нахождения абсцисс точек пересечения данных кривых
- 17. Площадь криволинейной трапеции, ограниченной кривой, заданной параметрически прямыми x=a, x=b и осью Ox (х(α)=а, х(β)=b), вычисляется
- 18. Пример. Вычислить площадь фигуры, ограниченной эллипсом Решение. Найдем сначала ¼ площади S.Здесь x изменяется от 0
- 19. Вычисление площадей в полярных координатах. Площадь S плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами
- 20. Пример. Найти площадь фигуры, ограниченной трехлепестковой розой: . Решение. Найдем сначала площадь половины одного лепестка розы,
- 21. Вычисление длины дуги в декартовых координатах. Теорема. Пусть кривая АВ задана уравнением y=f(x), где f(x) -
- 22. где xi-1 Следовательно, По теореме Лагранжа имеем Таким образом, длина вписанной ломаной равна
- 23. Пример. Найти длину дуги полукубической параболы y2 =x3 от начала координат до точки А(4;8) . Решение.
- 24. Длина дуги кривой, заданной параметрически уравнениями вычисляется по формуле
- 25. Пример. Вычислить длину астроиды Решение. Так как кривая симметрична относительно обеих координатных осей, то вычислим сначала
- 26. Длина дуги кривой в полярных координатах. Пусть в полярных координатах задано уравнение кривой r=r(φ); α≤φ≤β. Если
- 27. Пример. Найти длину кардиоиды r=a(1+cosφ). Решение. Кардиоида симметрична относительно полярной оси. Найдем половину длины кардиоиды. Таким
- 29. Скачать презентацию

![ЛИТЕРАТУРА [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/287409/slide-2.jpg)




![Приближенное значение работы на [a;b] есть Это приближенное равенство тем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/287409/slide-7.jpg)




![Пусть на [a;b] заданы непрерывные функции y=f1(x) и y=f2(x) такие,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/287409/slide-13.jpg)













 Решение задач с помощью квадратных уравнений . 9 класс
Решение задач с помощью квадратных уравнений . 9 класс Конкурс красоты, ума и таланта. Мисс Математика
Конкурс красоты, ума и таланта. Мисс Математика Урок Величины (юбилею школы посвящается)
Урок Величины (юбилею школы посвящается) Проценты в реальной жизни
Проценты в реальной жизни Определенный интеграл. Формула Ньютона-Лейбница
Определенный интеграл. Формула Ньютона-Лейбница Касательная к окружности
Касательная к окружности Многоугольники. 5 класс
Многоугольники. 5 класс Сфера. Уравнение сферы
Сфера. Уравнение сферы Геометрияның негізгі ұғымдары
Геометрияның негізгі ұғымдары Матричная алгебра в экономике
Матричная алгебра в экономике Второй признак равенства треугольников
Второй признак равенства треугольников Функция. Свойства функции
Функция. Свойства функции 02.2022 матем
02.2022 матем Аксонометрические проекции. Черчение
Аксонометрические проекции. Черчение Статистические гипотезы. Параметрические критерии. (Лекция 5)
Статистические гипотезы. Параметрические критерии. (Лекция 5) Введение в эконометрику
Введение в эконометрику Числа от 1 до 20
Числа от 1 до 20 Уравнение. 5 класс
Уравнение. 5 класс Алгебра. Исторический очерк
Алгебра. Исторический очерк Инновационный подход к актуализации экологического компонента в математике
Инновационный подход к актуализации экологического компонента в математике Приёмы устных вычислений в пределах 1000. Закрепление
Приёмы устных вычислений в пределах 1000. Закрепление Время
Время Текстовые задачи. Задачи на движение по окружности
Текстовые задачи. Задачи на движение по окружности Евклидова геометрия
Евклидова геометрия Симметрия в природе
Симметрия в природе Понятие о доказательной медицине. Случайное событие. Определение вероятности. Лекция 2
Понятие о доказательной медицине. Случайное событие. Определение вероятности. Лекция 2 Величины. Длина. (1 класс)
Величины. Длина. (1 класс) презентация к уроку №83
презентация к уроку №83