Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла презентация

рассмотреть понятия радианной меры угла, вращательного движения, синуса, косинуса, тангенса, котангенса угла, основные тригонометрические тождества, формулы приведения
Цели урока:
формировать умения применять тригонометрические тождества, формулы приведения

Что такое тригонометрия?
Тригономе́трия (от др.-греч. (от др.-греч. τρίγωνον «треугольник (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю») — раздел математики (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю») — раздел математики, в котором изучаются тригонометрические функции (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю») — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю») — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю») — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю») — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии для вычисления одних элементов треугольника по данным о других его элементах.

Рассмотрим окружность радиуса R и отметим на ней дугу РМ длины R и угол РОМ.
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.
Градусная мера угла в 1 радиан равна:
Так как π = 3,14, то 1 рад ≈57,3°.
Если угол содержит а радиан, то его градусная мера равна:

1 рад = 180°/π ≈ 57,3°. И наоборот, 1° = π/180 рад.
При повороте против часовой стрелки угол поворота считают положительным, а при повороте по часовой стрелке – отрицательным.
Если 0° < α < 90°, то α – угол I четверти, если 90° < α < 180°, то α – угол II четверти, если 180° < α < 270°, то α – угол III четверти, если 270° < α < 360°, то α – угол IV четверти.
Разным углам может соответствовать одна точка на окружности. Например, углы 0, 2π, 4π находятся в начале отсчета, т.е. в точке (1;0).

IV
II
III
I

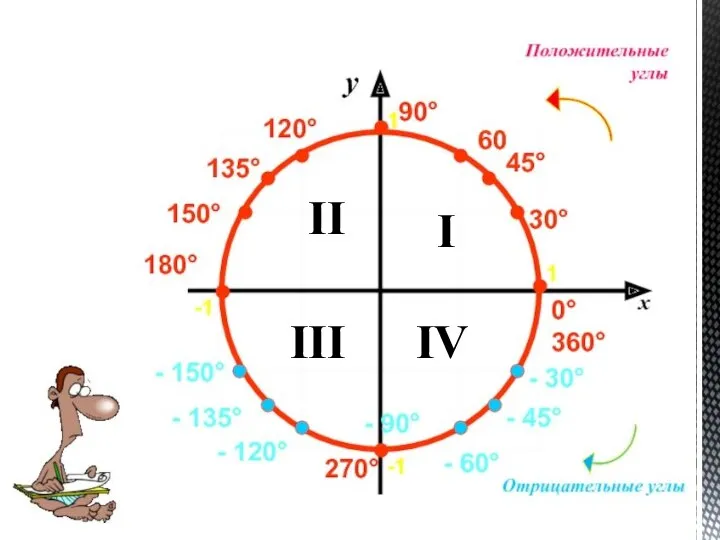
Синусом угла α называется отношение ординаты точки A к длине отрезка OA. Обозначают
sin α = OC/OA. Так как длина отрезка OA = 1, то sin α = ОC=у.
Косинусом угла α называется отношение абсциссы точки A к длине отрезка OA. Обозначают cos α = OB/OA. Так как длина отрезка OA = 1, то cos α = OB=х
Тангенсом угла α называется отношение ординаты точки A к абсциссе точки A. Обозначают tg α = OC/OB. Так как OC = sin α, OB = cos α, то tg α = sin α/cos α.
Котангенсом угла α называется отношение абсциссы точки A к ординате точки A. Обозначают ctg α = OB/OC. Так как OC = sin α, OB = cos α, то ctg α = cos α/sin α.
Котангенс равен обратному значению тангенса: ctg α = 1/tg α.
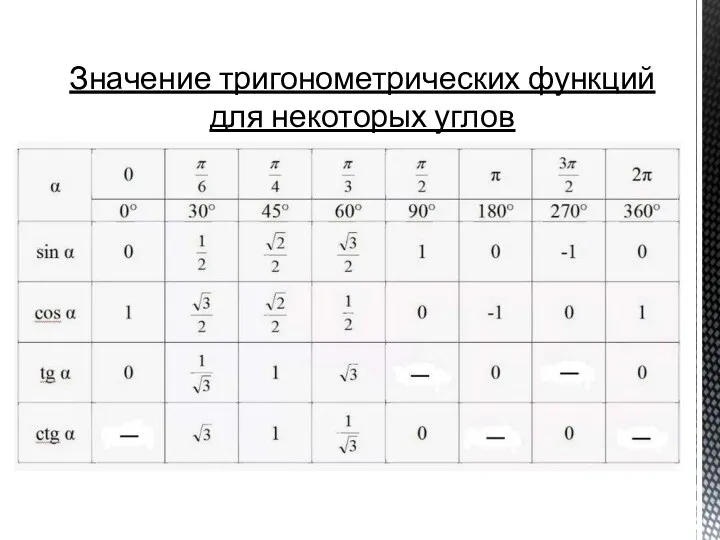
Из определения следует: если cos α = 0, то тангенс этого угла (α) не существует. Аналогично для котангенса: если sin α = 0, то котангенс этого угла (α) не существует.

Значение тригонометрических функций для некоторых углов

Функция cos является четной функцией.
Функции: sin, tg, ctg – нечётные функции.
cos (-x) = cos x;
sin (-x) = - sin x;
tg (-x) = - tg x;
ctg (-x) = - ctg x.
cos (-300) = cos 300;
sin (-450) = - sin 450;
tg (-600) = - tg 600;
ctg (-750) = - ctg 750.

Задача 1. Найдите градусную меру угла равного π радиан,
π/2 радиан, 3π/4 рад.
Решение: по формуле:
π радиан = 1800; π/2 радиан = 900, 3π/4 рад = 1350.
Найдём радианную меру угла в 10. Так как угол 1800 равен π радиан, то:
Если угол содержит α градусов, то его радианная мера составляет:

Задача 2. Найдите радианную меру угла равного 450, 150
Решение:

Площадь кругового сектора радиу­са R, образованного углом в π рад, равна:
Длина дуги, радиуса R, стягиваемая центральным углом α, вычисляется по формуле:

Задача 3. Найти радианную меру угла, выраженного в градусах: 1) 40°; 2) 120°; 3) 150°
Задача 4. Найти градусную меру угла, выраженного в радианах:
.

Задача 5. Вычислить радиус окружности, если дуга длиной 0,36 м стя­гивает центральный угол в 0,9 рад.
Задача 6. Найти радианную меру угла, стягиваемого дугой окружно­сти длиной 3 см, если радиус окружности равен 1,5 см.

Задача 7. Дуга кругового сектора стягивает угол в 3π/4 рад. Найти площадь сектора, если радиус круга равен 1 см.
Задача 10. Определите в какой четверти заключается угол α, если: а) α = 1200; б) α = 4350; в) α = - 2800
Задача 14. Найдите значение выражения: