Содержание
- 2. Основные понятия Оптимизация — это целенаправленная деятельность, заключающаяся о получении наилучших результатов при соответствующих условиях. Постановку
- 3. Наиболее сложной проблемой данного решения является постановка задачи оптимизации. Неправильная постановка приводит к ошибочным результатам или
- 4. Правильная постановка оптимальной задачи в этом случае должна звучать так : «Получить максимальный выход продукции при
- 5. Как вариант можно использовать критерий оптимизации, который будет учитывать эти оба параметра одновременно. Например с использованием
- 6. Математическая постановка Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции
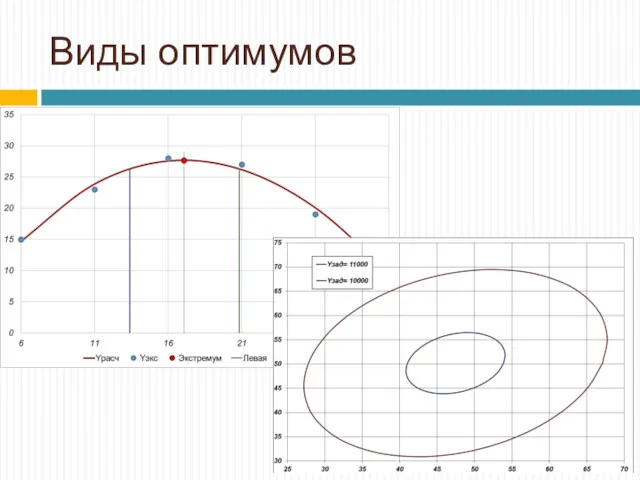
- 7. Виды оптимумов
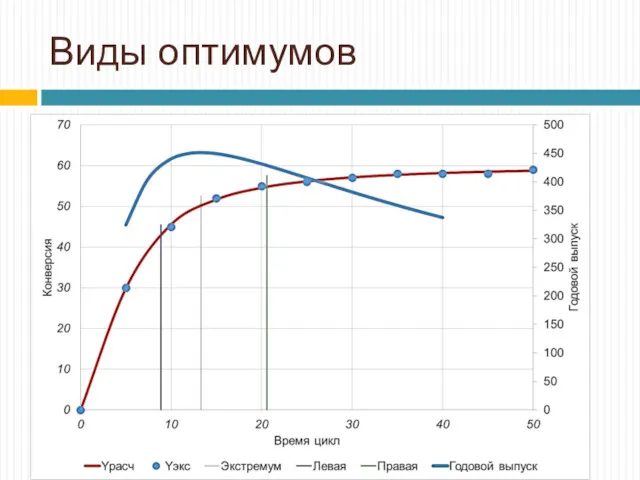
- 8. Виды оптимумов
- 9. Постановка задачи оптимизации В процессе проектирования ставится обычно задача определения наилучших значения параметров объектов для получения
- 10. Классификация методов оптимизации Методы оптимизации классифицируют в соответствии с задачами оптимизации: Локальные методы: сходятся к какому-нибудь
- 11. Классификация методов оптимизации Существующие в настоящее время методы поиска можно разбить на три большие группы функций:
- 12. Классификация методов оптимизации По размерности методы оптимизации делят на: методы одномерной оптимизации, когда функция зависит от
- 13. Классификация методов оптимизации По вычислительным возможностям делятся на: прямые методы, требующие только вычислений целевой функции в
- 14. Классификация численных методов оптимизации По виду целевой функции задачи оптимизации и методы их решения можно разделить
- 15. Реализация методов оптимизации Способ нахождения экстремума определяется классом задачи. Но перед тем, как получить математическую модель,
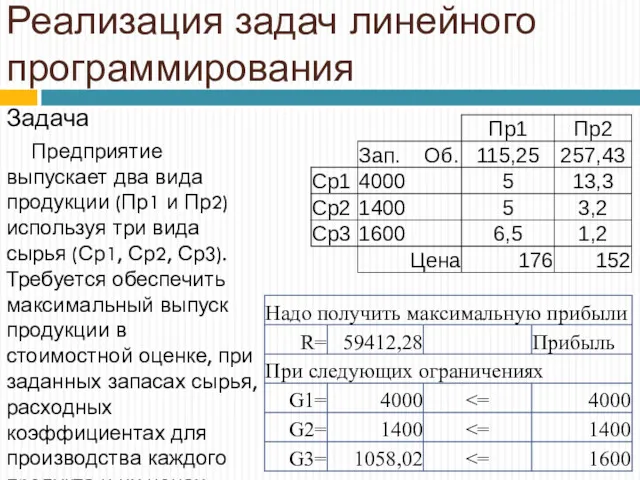
- 16. Реализация задач линейного программирования Задача Предприятие выпускает два вида продукции (Пр1 и Пр2) используя три вида
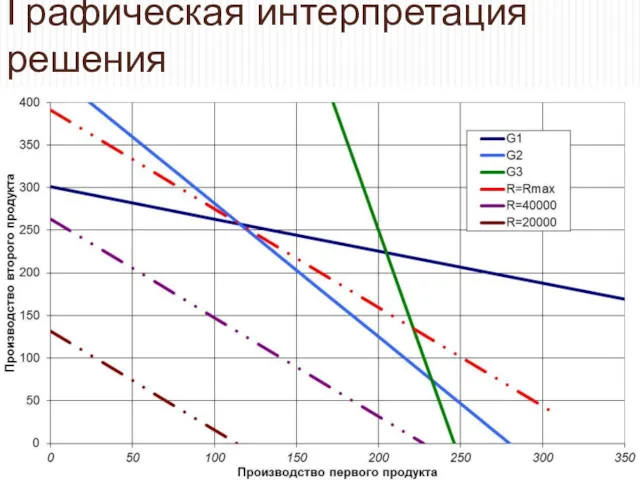
- 17. Графическая интерпретация решения
- 18. Другие задачи линейного программирования Транспортные задачи по доставке сырья и готовой продукции в разные точки (различная
- 19. Оптимизация экономических задач Любая задача оптимизации предполагает наличие конкурирующий процессов: Количество и качество продукции; Количество продукции
- 20. Оценка эффективности производства Общую оценку экономической эффективности процесса производят по следующим показателям: Производительность В, объем выпускаемой
- 21. sпр – себестоимость продукции; Sc – затраты на сырье, которые пропорциональны производительности и могут учитываться через
- 22. Sп – затраты на постоянные расходы включает в себя стоимость основных средств Ф и затраты на
- 23. Подставив все сделанные выводы можно получить окончательную формулу для расчета себестоимости продукта, которая и должна лежать
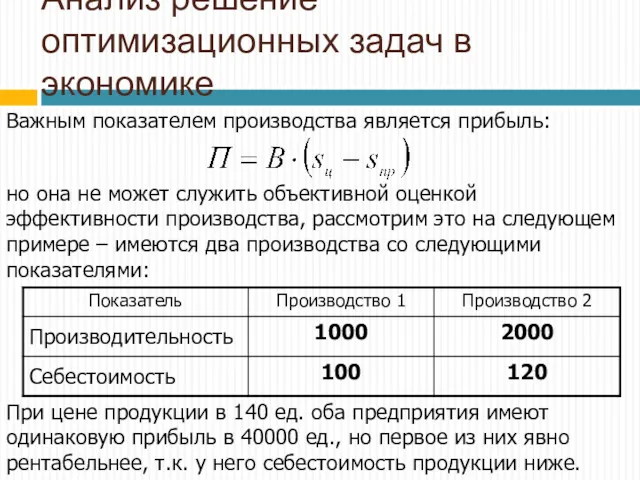
- 24. Анализ решение оптимизационных задач в экономике Важным показателем производства является прибыль: но она не может служить
- 25. Для более полной оценки эффективности надо используем норму прибыли согласно формулы: по ней мы получим 40%
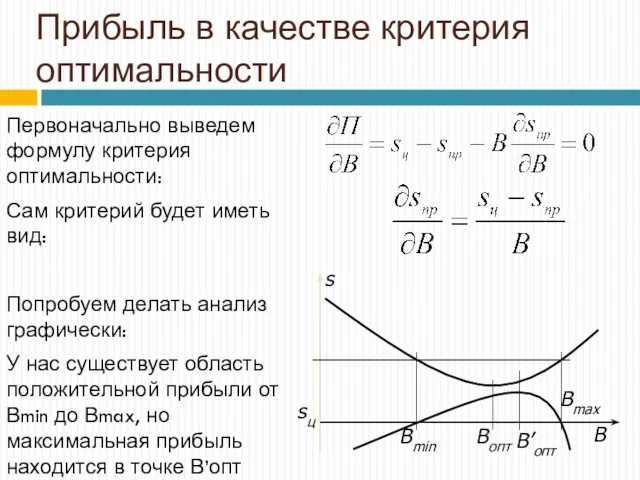
- 26. Прибыль в качестве критерия оптимальности Первоначально выведем формулу критерия оптимальности: Сам критерий будет иметь вид: Попробуем
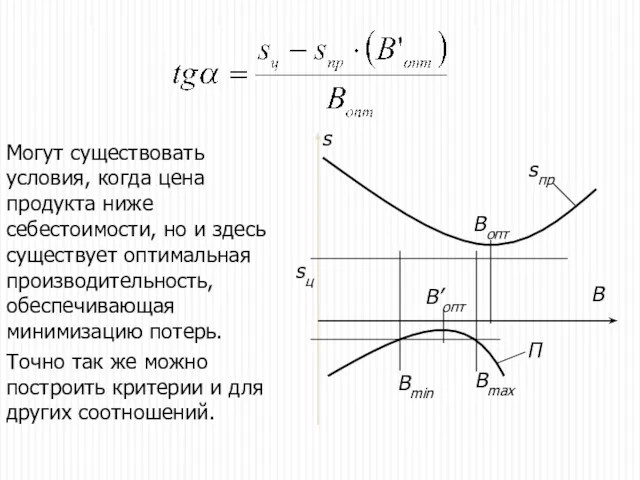
- 27. Могут существовать условия, когда цена продукта ниже себестоимости, но и здесь существует оптимальная производительность, обеспечивающая минимизацию
- 28. Так норма прибыли будет иметь вид: и даст результат как и оптимальная себестоимость Норма рентабельности капиталовложений
- 29. Примеры решения оптимальных задач в технике и жизни Задача: Предположим нам надо рассчитать потребности в материале
- 30. Решение: В начале запишем две формулы объема и площади поверхности для реактора: где: r – радиус,
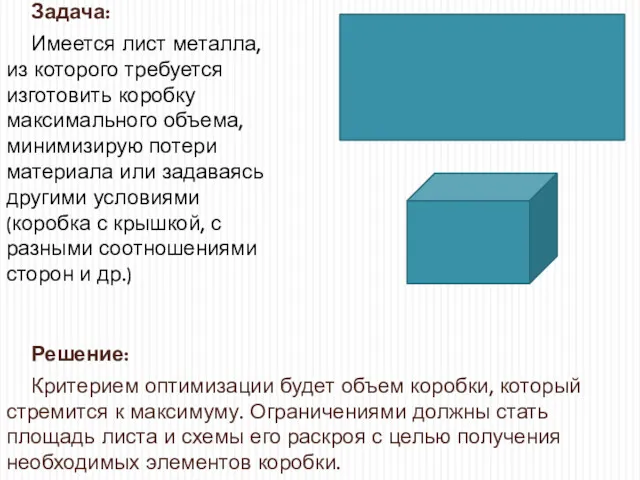
- 31. Задача: Имеется лист металла, из которого требуется изготовить коробку максимального объема, минимизирую потери материала или задаваясь
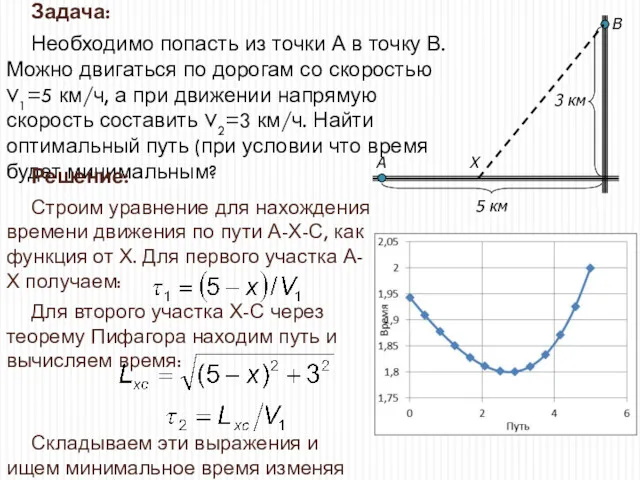
- 32. Задача: Необходимо попасть из точки А в точку В. Можно двигаться по дорогам со скоростью V1=5
- 33. Задача: Условия предыдущей задачи может быть усложнена. Например можно искать оптимальную стратегию движения по трассе в
- 34. Многопараметрические задачи При оптимизации многопараметрических нелинейных задач возникают проблемы определения направления поиска лучшего значения через частные
- 35. Комплексный метод (основа) Данный метод позволяет совершить поиск оптимума произвольной функции (как заданной аналитически, так и
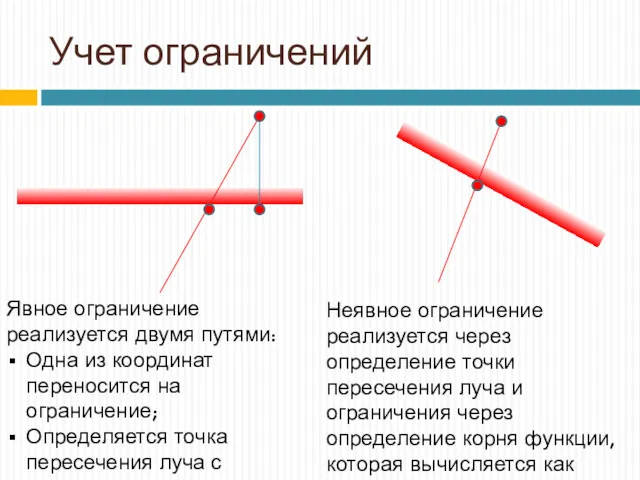
- 36. Комплексный метод (ограничения) Факторное пространство поиска может иметь следующие ограничения: Явными ограничения – которые просто вычисляются
- 38. Явное ограничение реализуется двумя путями: Одна из координат переносится на ограничение; Определяется точка пересечения луча с
- 39. Расчет завершается при достижении одного из двух критериев: Характерный размер комплекса меньше заданной погрешности работает в
- 41. Скачать презентацию




























 Скалярное произведение векторов
Скалярное произведение векторов Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний
Презентация Умножение двузначного числа на однозначное 3 класс Планета знаний Все действия с дробями. Урок математики в 5 классе
Все действия с дробями. Урок математики в 5 классе Презентация Молчанка (устный счет, 4 класс)
Презентация Молчанка (устный счет, 4 класс) Линейная функция и её график
Линейная функция и её график Презентация Математика вокруг нас
Презентация Математика вокруг нас Вычесть число 3.
Вычесть число 3. Понятие определенного интеграла
Понятие определенного интеграла Сызықтық емес (бейсызықтық) жұп регрессия
Сызықтық емес (бейсызықтық) жұп регрессия Дроби. Нахождение части числа. Нахождение целого по его части.
Дроби. Нахождение части числа. Нахождение целого по его части. Решение логических задач
Решение логических задач Знаходження невідомого зменшуваного
Знаходження невідомого зменшуваного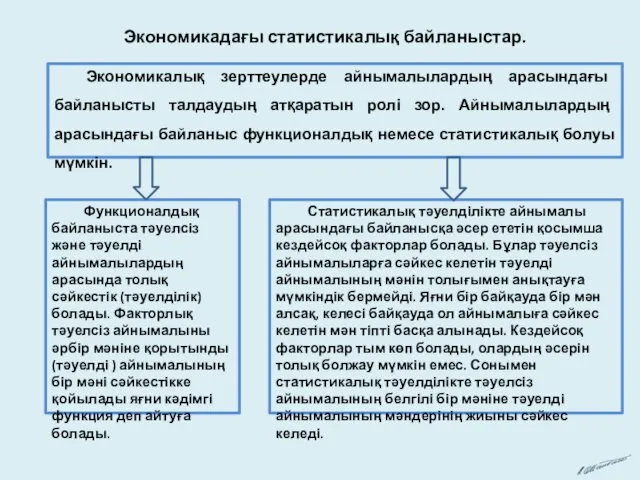 Экономикадағы статистикалық байланыстар
Экономикадағы статистикалық байланыстар Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Квадратные неравенства
Квадратные неравенства Тема урока: знаки > (больше), < (меньше)Математика 1 класс Диск
Тема урока: знаки > (больше), < (меньше)Математика 1 класс Диск Алгоритмические структуры
Алгоритмические структуры Обчислення виду 13 + 2. Задачі різних типів з одним сюжетом. Урок №81
Обчислення виду 13 + 2. Задачі різних типів з одним сюжетом. Урок №81 Решение уравнений (6 класс)
Решение уравнений (6 класс) Утворення, запис, читання чисел
Утворення, запис, читання чисел Единицы массы: тонна и центнер
Единицы массы: тонна и центнер Понятие алгоритма действий
Понятие алгоритма действий Симметрия в пространстве. Симметрия в природе и на практике
Симметрия в пространстве. Симметрия в природе и на практике Урок -викторина Счастливый случай. Параллельные прямые
Урок -викторина Счастливый случай. Параллельные прямые Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Разработка открытого урока математики
Разработка открытого урока математики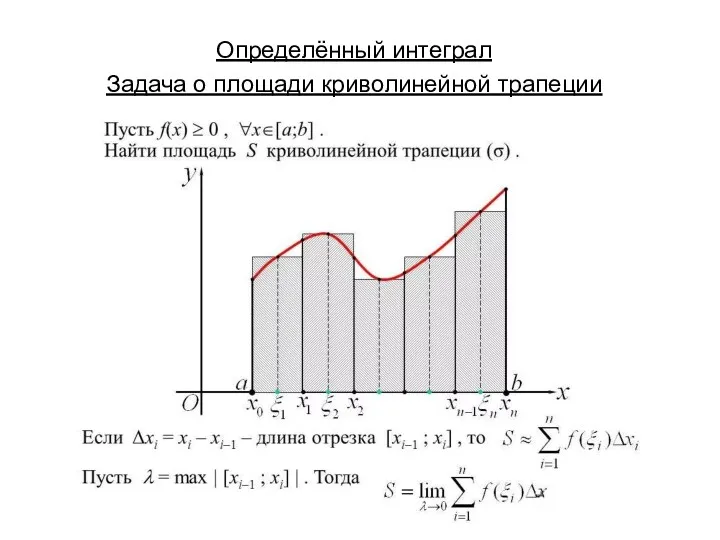 Определённый интеграл. Задача о площади криволинейной трапеции
Определённый интеграл. Задача о площади криволинейной трапеции Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач