Преобразование графиков функций презентация

Основные приёмы преобразования графиков
Параллельный перенос вдоль оси абсцисс
Параллельный перенос вдоль оси ординат
Растяжение и сжатие вдоль оси абсцисс
Растяжение и сжатие вдоль оси ординат
Преобразование симметрии относительно оси абсцисс
Преобразование симметрии относительно оси ординат
Построение графика функции у =│f(x)│
Построение графика функции у = f(│x│)

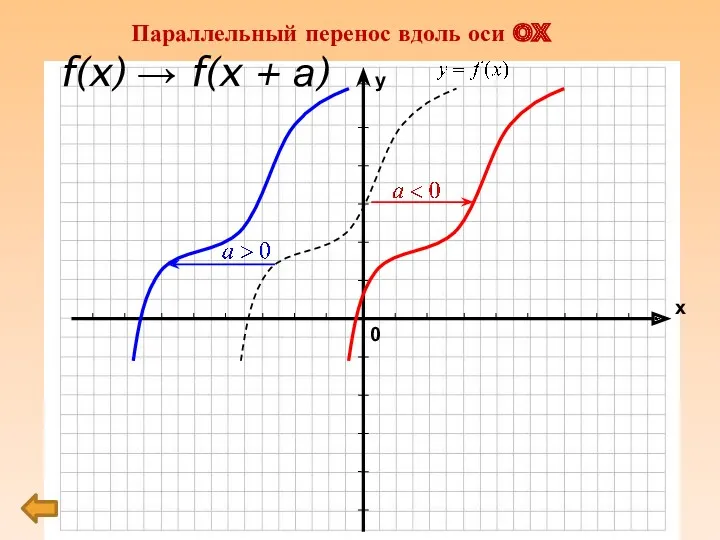
f(x) → f(x + а)
Параллельный перенос вдоль оси OX

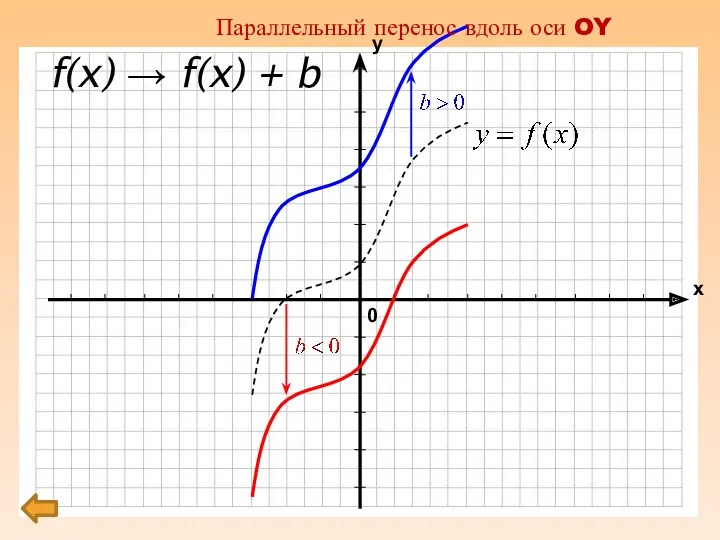
f(x) → f(x) + b
Параллельный перенос вдоль оси OY

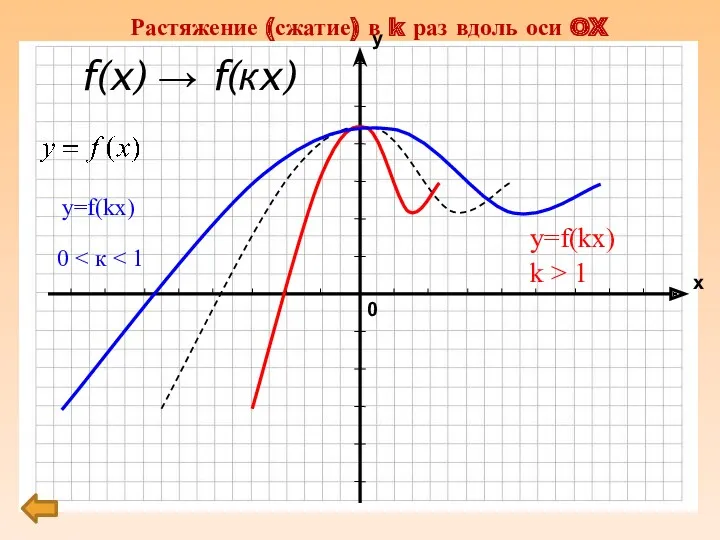
f(x) → f(кx)
y=f(kx)
k > 1
Растяжение (сжатие) в k раз вдоль оси OX
0 < к < 1
y=f(kx)

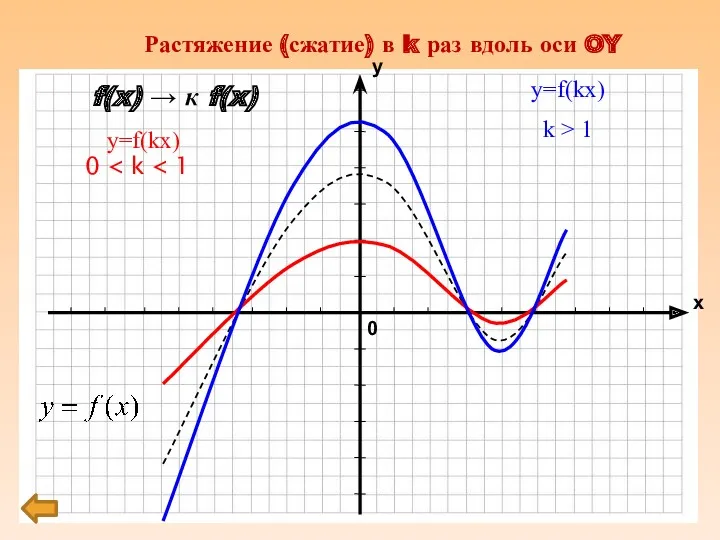
0 < k < 1
Растяжение (сжатие) в k раз вдоль оси OY
f(x) → к f(x)
y=f(kx)
k > 1
y=f(kx)

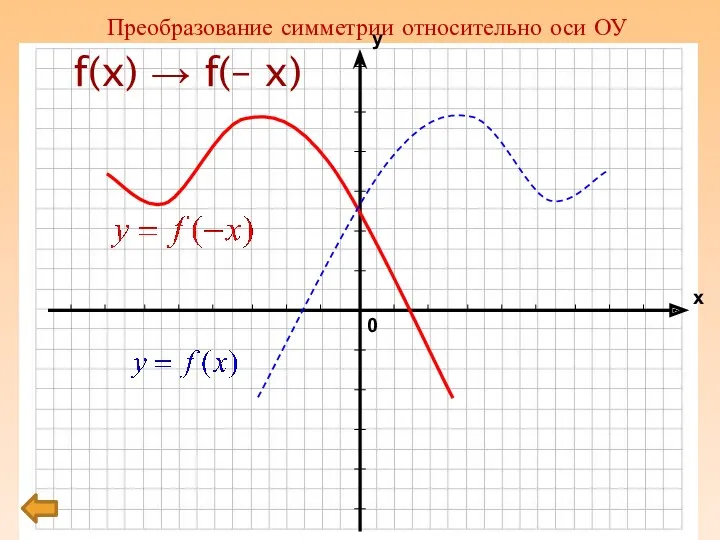
f(x) → f(– x)
Преобразование симметрии относительно оси ОУ

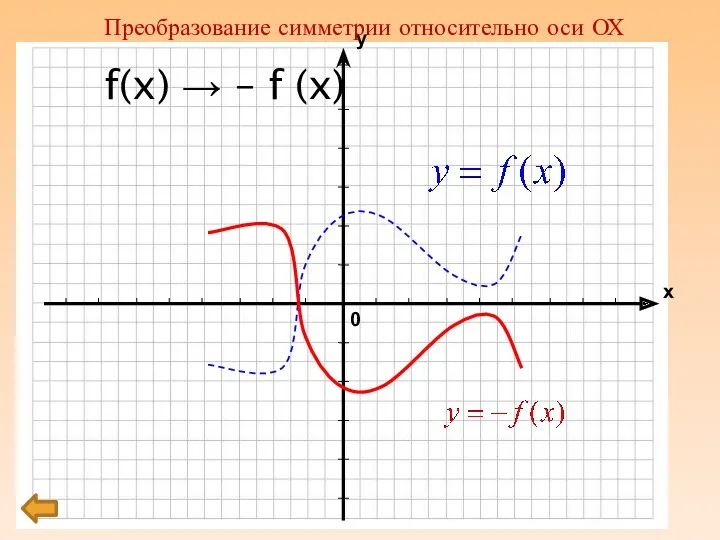
f(x) → – f (x)
Преобразование симметрии относительно оси ОХ