Содержание
- 2. Определение: Простым числом называется такое натуральное число, большее 1, которое имеет только два делителя – единицу
- 3. Например: Число 7 – простое. Число 2 – простое. (единственное простое четное число). Числа 3,11,19, 23,
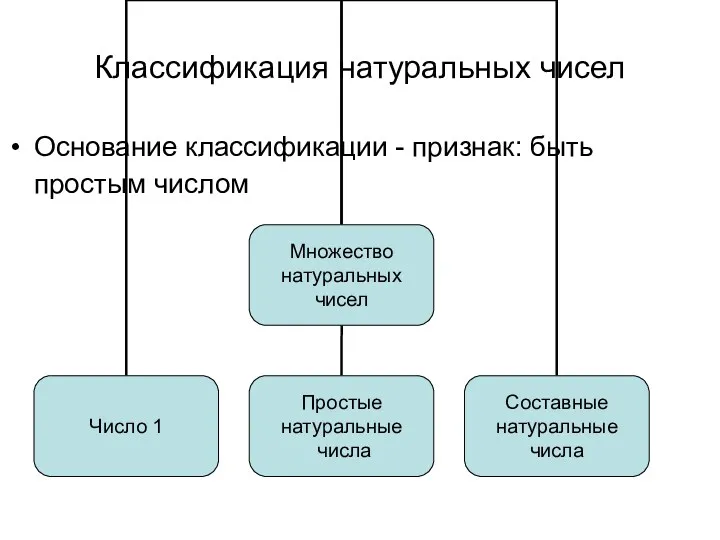
- 4. Классификация натуральных чисел Основание классификации - признак: быть простым числом
- 5. Свойства простых чисел Свойство1. Если простое число p делится на натуральное число n, отличное от 1,
- 6. Доказательство: Предположим, что число p – простое, p≠n, и делится на n. Тогда, по условию число
- 7. Свойство 2. Если p и g различные простые числа, то p не делится на g. Например:
- 8. Доказательство: Если p– простое число, то оно делится на 1 и p. По условию g-простое число,
- 9. Свойство 3. Если натуральное число a не делится на простое число p, то a и p
- 10. Доказательство: Пусть D(a;p)=d – наибольший общий делитель. Но p - простое число и не может делится
- 11. Если d=p, то а кратно p. Это противоречит условию. Значит, d=1, тогда числа a и p
- 12. Свойство 4. Если произведение двух натуральных чисел (a·b) делится на простое число p, то хотя бы
- 13. Доказательство: Пусть a и p взаимно простые числа (a не кратно p). Тогда по свойству делимости
- 14. Свойство 5. Если натуральное число больше 1, то оно имеет хотя бы один простой делитель. Например:
- 15. Доказательство: Предположим противное: пусть существуют натуральные числа, большие 1 и не имеющие ни одного простого делителя.
- 16. Если все элементы множества А есть натуральные числа, большие 1. Значит во множестве А есть наименьший
- 17. Число a>1, и оно либо простое, либо составное. Если a – простое, то оно не может
- 18. b Значит b не принадлежит множеству А, и следовательно, число b имеет простой делитель. Пусть этот
- 19. Число а кратно b, а число b кратно р, тогда число а кратно p (свойство транзитивности
- 20. Свойство 6. Наименьший простой делитель составного числа a не превосходит Определите, является ли число 137 простым
- 21. Действительно: Если р наименьший простой делитель числа а, то а=р·g. Так как р наименьший простой делитель,
- 22. Если натуральное число а, больше единицы, и не делится ни на одно из простых чисел, квадрат
- 23. Например: Определите является ли число 137 простым. 121 Выпишем все простые числа, не превышающие 11 Это
- 24. 137 не делится на 2 137 не делится на 3 137 не делится на 5 137
- 25. Определите, какие числа простые, а какие числа составные? 161, 252, 391, 837.
- 26. Эратосфен – греческий математик и астроном (III в. до н.э.) – способ определения простых чисел –
- 27. Теорема Эвклида: Множество простых чисел бесконечно. Доказательство: Предположим противное: множество простых чисел конечно. Всякое конечное множество
- 28. Обозначим множество простых чисел символом М. М={2,3,5,7,11,13,…p}, где p- самое большое простое число. Рассмотрим число а,
- 29. Число а либо простое, либо составное. Но число а не может быть простым по предположению, так
- 30. Основная теорема арифметики. Любое составное число можно единственным образом представить в виде произведения простых множителей
- 31. Теорема содержит два утверждения: 1. Разложение на простые множители любого составного натурального числа существует. 2. Разложение
- 32. Доказательство существования разложения Пусть а составное число. Тогда (по свойству 5 простых чисел) найдется простой делитель
- 33. Если -простое число, то составное число а представлено в виде простых множителей Если - составное, то
- 34. заметим, что Этот процесс конечен. Значит наступит момент, когда последний множитель в разложении составного числа a
- 35. В полученном разложении одинаковые множители могут повторятся. Например: 900=2·2·3·3·5·5
- 36. Единственность разложения составного числа на простые множители Доказать: разложение составных чисел на простые множители определено однозначно.
- 37. Доказательство: Пусть Тогда Правая часть равенства делится на Значит и левая часть делится на
- 38. По свойству 4 простых чисел один из множителей в левой части равенства делится Пусть это будет
- 39. Пусть Разделив обе части равенства Имеем: И так,
- 40. Продолжая рассуждения, придем: 1) при n=l к тому, что при делении на Все множители в левой
- 41. 2) при n Так как произведение простых чисел не может быть равно 1. 3) При n>l
- 42. Разложение составного числа а на простые множители называется каноническим представлением натурального числа. Задание: представьте число n=126
- 43. 126 2 63 3 21 3 7 7 1 Значит 126 =2·3·3·7
- 44. НОК(126; 54) 126 : 54=2 (ост. 18), тогда Представим 126 и 54 в каноническом виде.
- 45. 54 2 27 3 9 3 3 3 1
- 46. НОК (126;54)= НОД (126;54)=
- 48. Скачать презентацию










































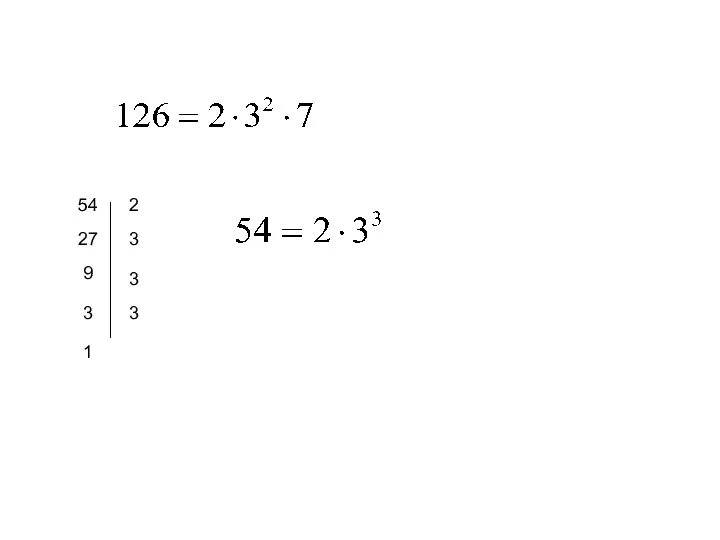

 Презентация к уроку по теме Теорема Пифагора
Презентация к уроку по теме Теорема Пифагора Алгебра и геометрия. Основные понятия
Алгебра и геометрия. Основные понятия Десятичные дроби. Урок - вернисаж
Десятичные дроби. Урок - вернисаж Геометрические фигуры и их свойства
Геометрические фигуры и их свойства Приемы вычитания с переходом через десяток. 1 класс
Приемы вычитания с переходом через десяток. 1 класс Решение задач на применение аксиом стереометрии и их следствий. Урок 4
Решение задач на применение аксиом стереометрии и их следствий. Урок 4 Презентация Путешествие Королевы Линейки
Презентация Путешествие Королевы Линейки Двугранный угол. Перпендикулярность плоскостей. Прямоугольный параллелепипед
Двугранный угол. Перпендикулярность плоскостей. Прямоугольный параллелепипед Дискретная математика
Дискретная математика Движение. Виды движений
Движение. Виды движений Математический диктант
Математический диктант Час занимательной математики
Час занимательной математики Тест по теме Геометрические фигуры 1-2 кл.
Тест по теме Геометрические фигуры 1-2 кл. Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел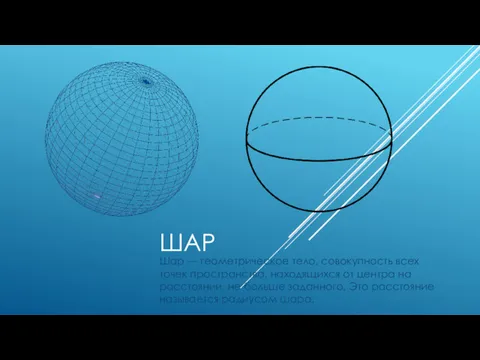 Шар. Объём шара
Шар. Объём шара Дифференциальные уравнения первого порядка
Дифференциальные уравнения первого порядка Основи математичної статистики
Основи математичної статистики Алгебраические дроби
Алгебраические дроби Урок – экскурсия. История космонавтики. Умножение десятичных дробей
Урок – экскурсия. История космонавтики. Умножение десятичных дробей Правильные многоугольники
Правильные многоугольники Комплексные числа. Типовой вариант самостоятельной работы
Комплексные числа. Типовой вариант самостоятельной работы Состав чисел
Состав чисел Правила умножения обыкновенных дробей
Правила умножения обыкновенных дробей Алгебра логики
Алгебра логики Вертикальные углы
Вертикальные углы Приемы письменного деления
Приемы письменного деления Проверка знаний по математике . 4 класс ( I полугодие)
Проверка знаний по математике . 4 класс ( I полугодие) Устный счёт
Устный счёт