Содержание
- 2. Общее уравнение прямой М0(х0; у0 ) Уравнение вида: Теорема с произвольными коэффициентами А; В; С такими
- 3. Общее уравнение прямой Найдем разность уравнений (1) и (2): Пусть точки М0(х0; у0 ) и М
- 4. Общее уравнение прямой Общее уравнение прямой называется полным, если все коэффициенты А, В, и С отличны
- 5. Уравнение прямой в отрезках Рассмотрим полное уравнение прямой: Обозначим: Получим: Уравнение в отрезках b a Уравнение
- 6. Каноническое уравнение прямой Любой ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Требуется найти
- 7. Каноническое уравнение прямой Пусть прямая проходит через две заданные и отличные друг от друга точки: М1(х1;
- 8. Уравнение прямой с угловым коэффициентом Уравнение прямой с угловым коэффициентом Уравнение прямой с угловым коэффициентом
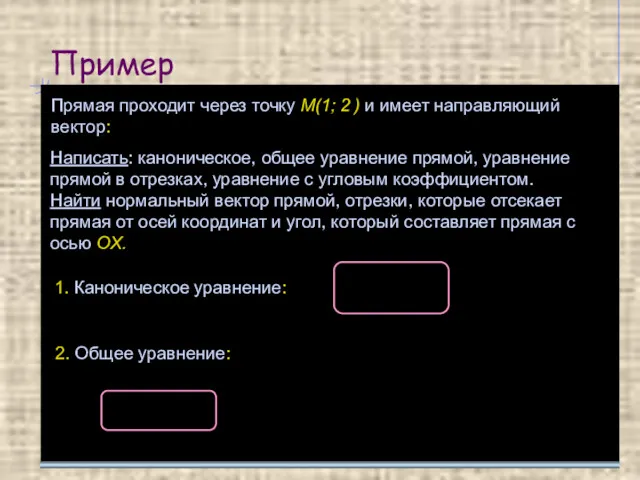
- 9. Пример Прямая проходит через точку М(1; 2 ) и имеет направляющий вектор: Написать: каноническое, общее уравнение
- 10. Пример 3. Уравнение в отрезках: 4. Уравнение с угловым коэффициентом: М b a
- 11. Угол между двумя прямыми Пусть две прямые L1 и L2 заданы общими уравнениями: Угол между этими
- 12. Угол между двумя прямыми Пусть две прямые L1 и L2 заданы каноническими уравнениями: Угол между этими
- 13. Угол между двумя прямыми Пусть две прямые L1 и L2 заданы уравнениями с угловыми коэффициентами:
- 14. Расстояние от точки до прямой Пусть необходимо найти расстояние от точки М0(х0; у0 ) до прямой,
- 15. Расстояние от точки до прямой Точка М1(х1; у1 ) принадлежит прямой L , следовательно:
- 16. Биссектриса углов между прямыми Пусть две прямые L1 и L2 заданы общими уравнениями: Если точка M(x;
- 17. Деление отрезка в заданном отношении Разделить отрезок М1М2 в заданном отношении λ > 0 значит найти
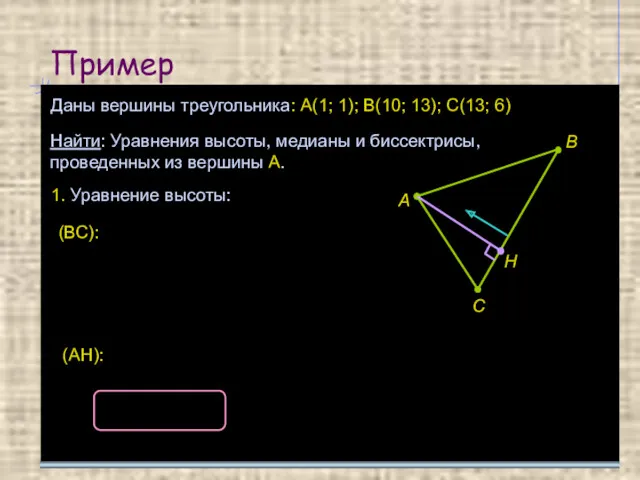
- 18. Пример Даны вершины треугольника: А(1; 1); В(10; 13); С(13; 6) Найти: Уравнения высоты, медианы и биссектрисы,
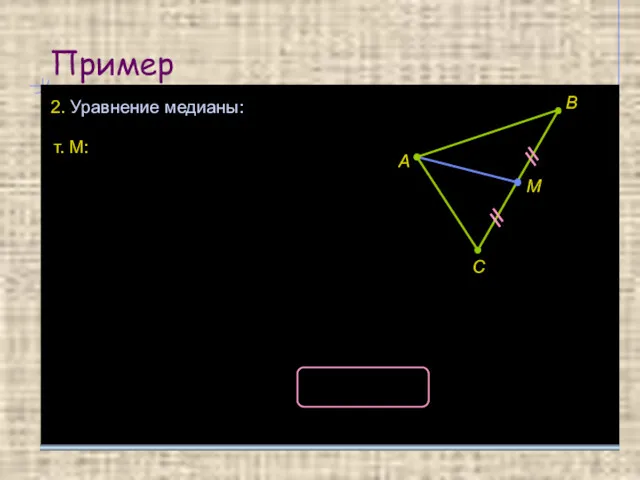
- 19. Пример 2. Уравнение медианы: А В С М т. М:
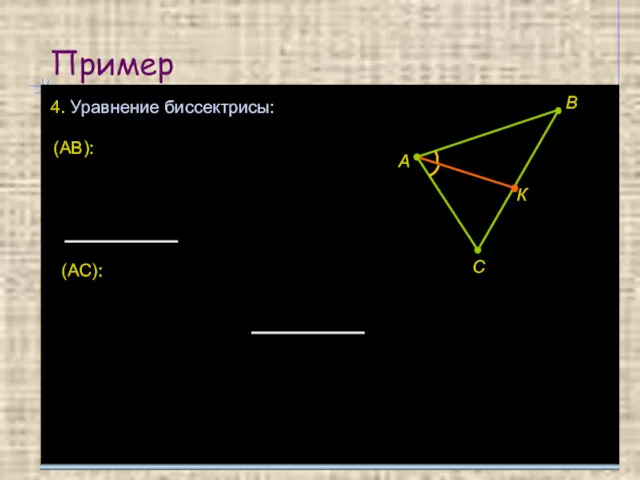
- 20. Пример 4. Уравнение биссектрисы: А В С К (АВ): (АС):
- 22. Скачать презентацию















 Презентация к уроку по теме Теорема Пифагора
Презентация к уроку по теме Теорема Пифагора Алгебра и геометрия. Основные понятия
Алгебра и геометрия. Основные понятия Десятичные дроби. Урок - вернисаж
Десятичные дроби. Урок - вернисаж Геометрические фигуры и их свойства
Геометрические фигуры и их свойства Приемы вычитания с переходом через десяток. 1 класс
Приемы вычитания с переходом через десяток. 1 класс Решение задач на применение аксиом стереометрии и их следствий. Урок 4
Решение задач на применение аксиом стереометрии и их следствий. Урок 4 Презентация Путешествие Королевы Линейки
Презентация Путешествие Королевы Линейки Двугранный угол. Перпендикулярность плоскостей. Прямоугольный параллелепипед
Двугранный угол. Перпендикулярность плоскостей. Прямоугольный параллелепипед Дискретная математика
Дискретная математика Движение. Виды движений
Движение. Виды движений Математический диктант
Математический диктант Час занимательной математики
Час занимательной математики Тест по теме Геометрические фигуры 1-2 кл.
Тест по теме Геометрические фигуры 1-2 кл. Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел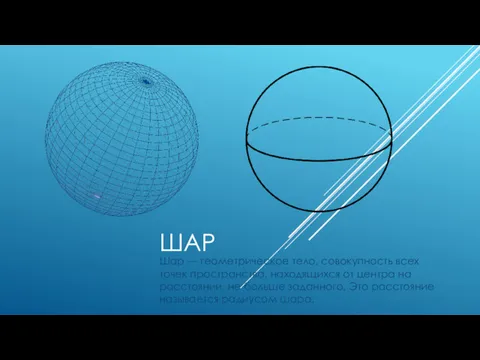 Шар. Объём шара
Шар. Объём шара Дифференциальные уравнения первого порядка
Дифференциальные уравнения первого порядка Основи математичної статистики
Основи математичної статистики Алгебраические дроби
Алгебраические дроби Урок – экскурсия. История космонавтики. Умножение десятичных дробей
Урок – экскурсия. История космонавтики. Умножение десятичных дробей Правильные многоугольники
Правильные многоугольники Комплексные числа. Типовой вариант самостоятельной работы
Комплексные числа. Типовой вариант самостоятельной работы Состав чисел
Состав чисел Правила умножения обыкновенных дробей
Правила умножения обыкновенных дробей Алгебра логики
Алгебра логики Вертикальные углы
Вертикальные углы Приемы письменного деления
Приемы письменного деления Проверка знаний по математике . 4 класс ( I полугодие)
Проверка знаний по математике . 4 класс ( I полугодие) Устный счёт
Устный счёт