Содержание
- 2. «Приобретать знания – храбрость, приумножать их – мудрость, а умело применять – великое искусство» (восточная мудрость)
- 3. Если то решений нет I. Простейшие тригонометрические уравнения.
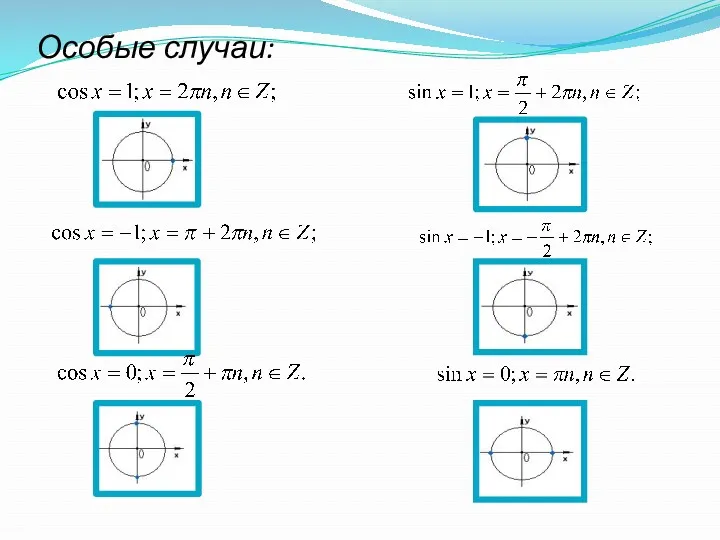
- 4. Особые случаи:
- 5. Уравнения вида
- 6. Укажите общую формулу, по которой находятся все корни уравнения 1 вариант 2 вариант
- 7. Типы тригонометрических уравнений
- 8. Примеры решения тригонометрических уравнений
- 10. sin 2x + sin x= 0 sin 2x = 2 sin x cos x 2 sin
- 11. 4 tg x – 3 ctg x = 1 ctg x = 1/ tg x
- 13. Один из способов решения такого уравнения состоит в том, что левую часть уравнения можно преобразовать по
- 14. 2cos3х + 4 sin(х/2) = 7 Укажите число корней уравнения на промежутке [0; 2π]: sinх =
- 15. Для решения задач повышенной сложности в алгебре используются нестандартные методы решения. Один из таких методов –
- 16. Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим. Мажорантой функции f(х) на
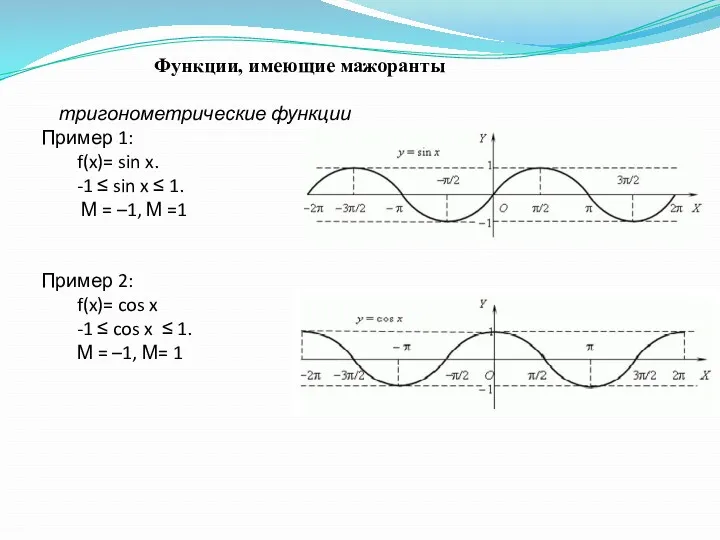
- 17. Функции, имеющие мажоранты тригонометрические функции Пример 1: f(x)= sin x. -1 ≤ sin x ≤ 1.
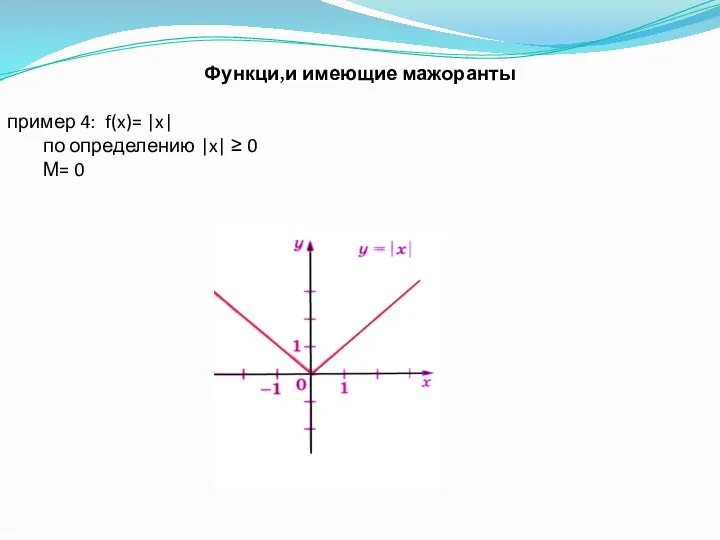
- 18. Функци,и имеющие мажоранты пример 4: f(x)= |x| по определению |x| ≥ 0 М= 0
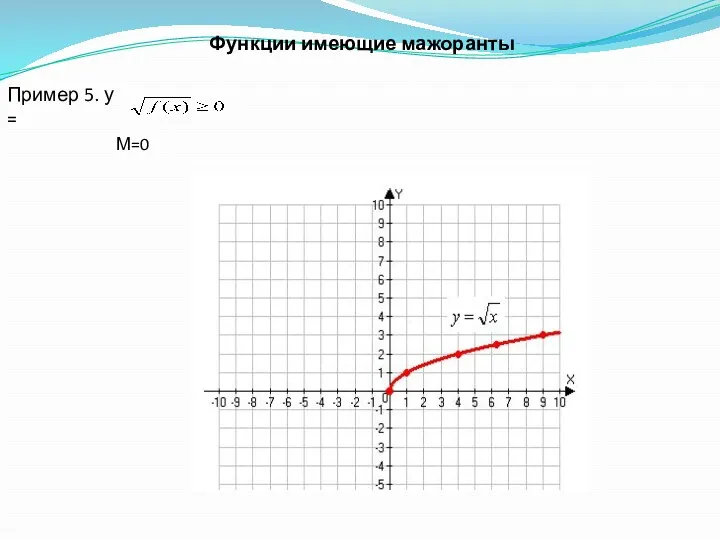
- 19. Пример 5. у = Функции имеющие мажоранты М=0
- 20. 2. Метод мажорант Пусть мы имеем уравнение и существует такое число М, что для любого Х
- 21. Пример Оценим левую и правую части уравнения: Равенство будет выполняться, если обе части = 4.
- 22. Решим первое уравнение системы: Проверим, является ли найденное число корнем второго уравнения системы: - верно Ответ:
- 24. Скачать презентацию







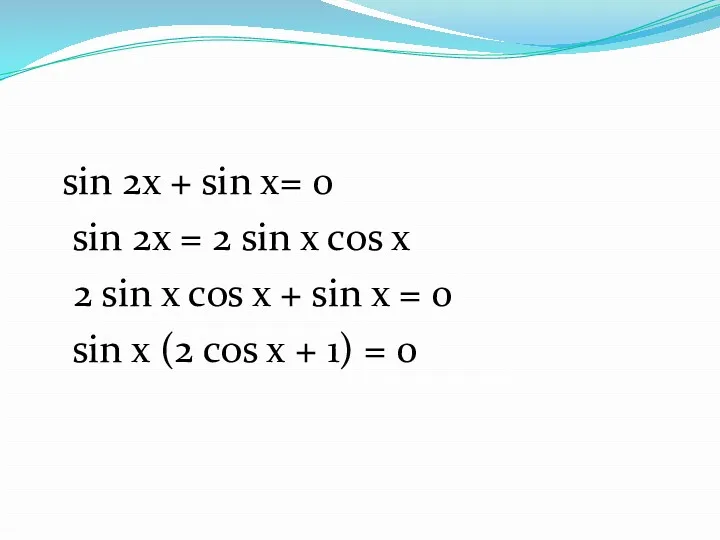









 Решение задач с помощью квадратных уравнений . 9 класс
Решение задач с помощью квадратных уравнений . 9 класс Конкурс красоты, ума и таланта. Мисс Математика
Конкурс красоты, ума и таланта. Мисс Математика Урок Величины (юбилею школы посвящается)
Урок Величины (юбилею школы посвящается) Проценты в реальной жизни
Проценты в реальной жизни Определенный интеграл. Формула Ньютона-Лейбница
Определенный интеграл. Формула Ньютона-Лейбница Касательная к окружности
Касательная к окружности Многоугольники. 5 класс
Многоугольники. 5 класс Сфера. Уравнение сферы
Сфера. Уравнение сферы Геометрияның негізгі ұғымдары
Геометрияның негізгі ұғымдары Матричная алгебра в экономике
Матричная алгебра в экономике Второй признак равенства треугольников
Второй признак равенства треугольников Функция. Свойства функции
Функция. Свойства функции 02.2022 матем
02.2022 матем Аксонометрические проекции. Черчение
Аксонометрические проекции. Черчение Статистические гипотезы. Параметрические критерии. (Лекция 5)
Статистические гипотезы. Параметрические критерии. (Лекция 5) Введение в эконометрику
Введение в эконометрику Числа от 1 до 20
Числа от 1 до 20 Уравнение. 5 класс
Уравнение. 5 класс Алгебра. Исторический очерк
Алгебра. Исторический очерк Инновационный подход к актуализации экологического компонента в математике
Инновационный подход к актуализации экологического компонента в математике Приёмы устных вычислений в пределах 1000. Закрепление
Приёмы устных вычислений в пределах 1000. Закрепление Время
Время Текстовые задачи. Задачи на движение по окружности
Текстовые задачи. Задачи на движение по окружности Евклидова геометрия
Евклидова геометрия Симметрия в природе
Симметрия в природе Понятие о доказательной медицине. Случайное событие. Определение вероятности. Лекция 2
Понятие о доказательной медицине. Случайное событие. Определение вероятности. Лекция 2 Величины. Длина. (1 класс)
Величины. Длина. (1 класс) презентация к уроку №83
презентация к уроку №83