Грани конгруэнтны. Скрещивающиеся ребра попарно равны.
Трехгранные углы равны. Противолежащие двугранные углы
равны.
Два плоских угла, опирающихся на одно ребро, равны.
Сумма плоских углов при каждой вершине равна 180°.
Развертка тетраэдра - треугольник или параллелограмм.
Описанный параллелепипед прямоугольный.
Тетраэдр имеет три оси симметрии.
Общие перпендикуляры скрещивающихся ребер попарно
перпендикулярны.
Средние линии попарно перпендикулярны.
Периметры , площади, высота граней равны.
Отрезки, соединяющие вершины с центрами тяжести противоположных граней, равны.
Радиусы описанных около граней окружностей равны.
Центр тяжести тетраэдра совпадает с центром описанной сферы.
Центр тяжести совпадает с центром вписанной сферы.
Центр описанной сферы совпадает с центром вписанной.
Вписанная сфера касается граней в центрах описанных около этих
граней окружностей.
Сумма всех двугранных углов равна нулю.
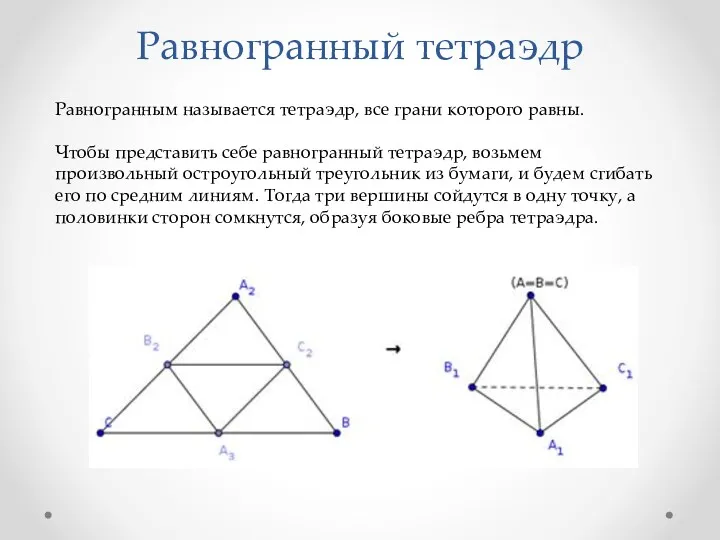
Свойства равногранного тетраэдра




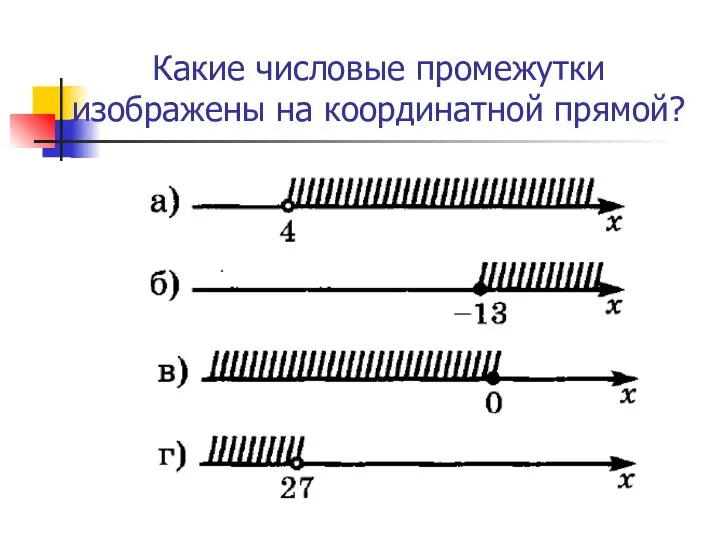 Числовые промежутки (часть 1)
Числовые промежутки (часть 1) Доли. Обыкновенные дроби
Доли. Обыкновенные дроби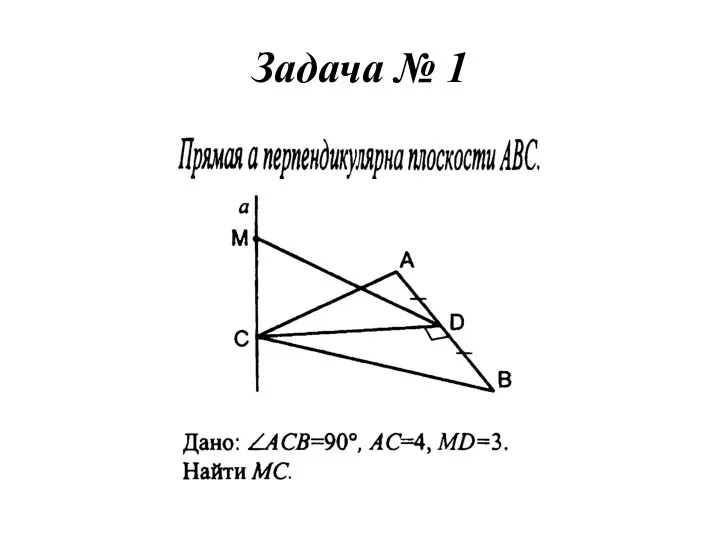 Прямая и плоскость. Задачи
Прямая и плоскость. Задачи Необычные и старинные способы умножения
Необычные и старинные способы умножения Производная функции. Производная линейной функции
Производная функции. Производная линейной функции Презентация для учащихся 2 класса по математике (автор Л.Г. Петерсон) Такая загадочная Индия
Презентация для учащихся 2 класса по математике (автор Л.Г. Петерсон) Такая загадочная Индия Математический проект Час за часом
Математический проект Час за часом Отношение величин математика. 6 класс
Отношение величин математика. 6 класс Методика обучения младших школьников решению задач на движение
Методика обучения младших школьников решению задач на движение Простейшие задачи в координатах
Простейшие задачи в координатах Алгебраическая Своя игра для любителей математики (8 класс)
Алгебраическая Своя игра для любителей математики (8 класс) Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Корреляционный анализ данных. Лекция 9
Корреляционный анализ данных. Лекция 9 Решение систем уравнений второй степени
Решение систем уравнений второй степени Понятие о корреляционном и регрессионном анализах
Понятие о корреляционном и регрессионном анализах Потребительская корзина. Исследование по математике
Потребительская корзина. Исследование по математике Математические методы моделирования и прогнозирования экономических процессов
Математические методы моделирования и прогнозирования экономических процессов Решение планиметрических многовариантных задач
Решение планиметрических многовариантных задач Работа по геометрии Ортоцентрический треугольник (пояснительная записка + презентация)
Работа по геометрии Ортоцентрический треугольник (пояснительная записка + презентация) Функции нескольких переменных
Функции нескольких переменных Игра-тренажер по математике.
Игра-тренажер по математике. Разложение многочлена на множители с помощью комбинации различных приемов
Разложение многочлена на множители с помощью комбинации различных приемов Производная функции
Производная функции Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Приёмы письменных вычислений (3 класс)
Приёмы письменных вычислений (3 класс) Случаи сложения и вычитания, основанные на знании нумерации чисел
Случаи сложения и вычитания, основанные на знании нумерации чисел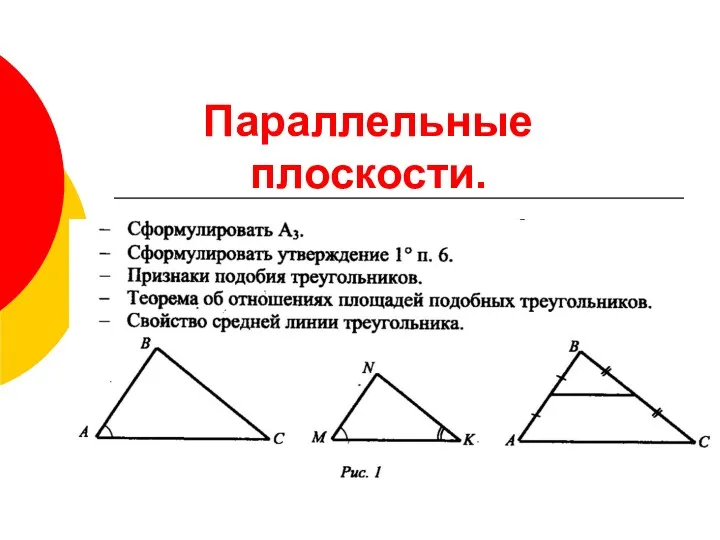 Параллельные плоскости
Параллельные плоскости Построение графика квадратичной функции. (9 класс)
Построение графика квадратичной функции. (9 класс)