Содержание
- 2. Recurrences Let (x0, x1, x2, ...) be an infinite sequence of numbers in that several initial
- 3. Examples 1) Initial element: x0 = 1, recurrence: xn = xn -1 + 1 for n
- 4. 2) Initial element: x0 = 1, recurrence: xn = 2xn -1 for n > 0. We
- 5. First order linear recurrences The general linear recurrence of the first order has the form where
- 6. Any element xn, n > 0, is uniquely defined by a, b, and x0. Can we
- 7. 1. a = 1. The equation has the form We can find ... Obviously, This sequence
- 8. 2. b = 0. The equation has the form We can find ... Obviously, This sequence
- 9. Now we consider the general case First we shall reduce the equation to a simplified form
- 10. Let us select such s that i.e. Note that for a = 1 this expression is
- 11. This equation has a simplest form (case 2), its solution is Because of we obtain and
- 12. We don't recommend you to remember this formula. It is rather the solution method. It includes
- 13. Note that the solution has the form where c1 and c2 are some constants. We see
- 14. Example: Towers of Hanoi The French mathematician Edouard Lucas invents in 1883 the following problem. Eight
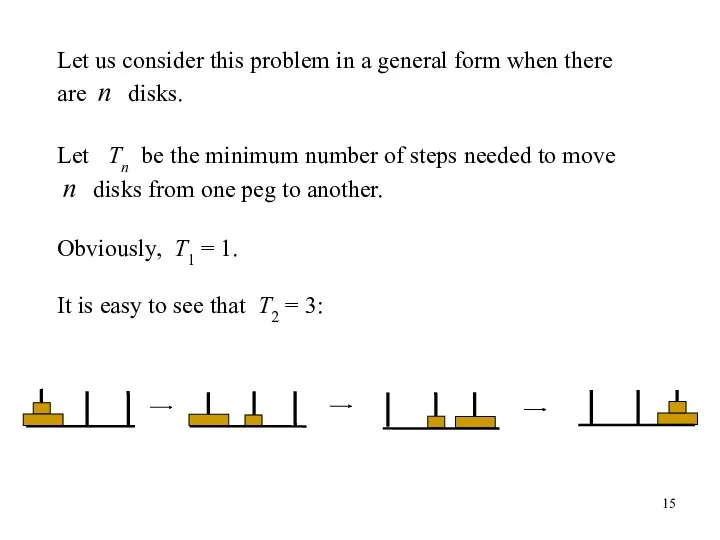
- 15. Let us consider this problem in a general form when there are n disks. Let Tn
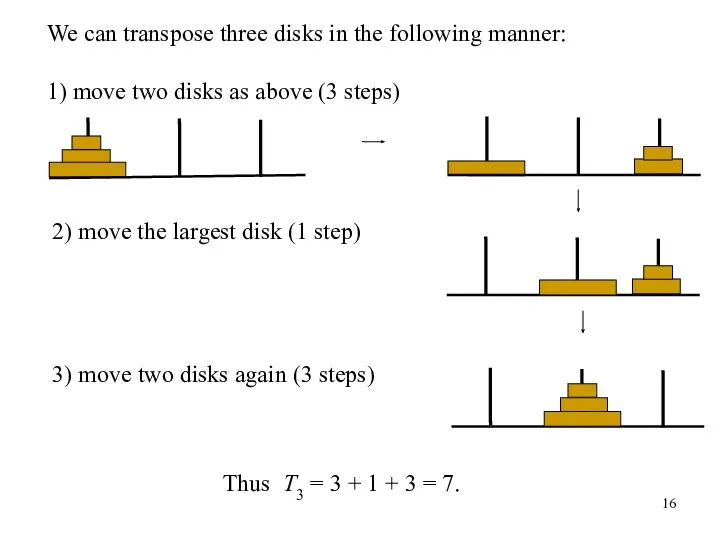
- 16. We can transpose three disks in the following manner: 1) move two disks as above (3
- 17. In general case we must transpose n – 1 smaller disks before we move the largest
- 18. We solve this equation in three described stage. 1. Reduction. then Let Take s = −
- 19. Second order linear recurrences General linear recurrence equation of second order has the form where a,
- 20. If we know the two initial elements x0 and x1 then we are able to compute
- 21. We shall look for a solution in the exponential form: where α is unknown constant (the
- 22. Thus α must be a root of the equation called a characteristic equation. There are the
- 23. A. The characteristic equation has two distinct roots α1 and α2. Then both sequences and satisfy
- 24. The homogeneous linear equation has two following important properties: 1) if a sequence satisfies the equation
- 25. both satisfy the equation (3) then the sequence also satisfies this equation. 2) if sequences and
- 26. Due to properties 1), 2) we may affirm that the sequence satisfies the equation (3) for
- 27. Thus we get a system of two linear equations with two unknowns c1, c2: The determinant
- 28. B. The characteristic equation has a single root α. In this case the general solution has
- 29. So we have the following algorithm for solving of a linear homogeneous recurrence equation of the
- 30. Examples 1) The characteristic equation: Roots: The general solution: Equations for c1, c2: Solution of the
- 31. Examples 2) The characteristic equation: Unique root: The general solution: Equations for c1, c2: Solution of
- 32. Inhomogeneous equation An inhomogeneous linear recurrence of the second order may be reduced to homogeneous equation
- 33. If a + b ≠ 1 then s exist and we obtain a homogeneous equation, solve
- 34. Fibonacci numbers Leonardo Fibonacci (1170 – 1250) also known as Leonardo Pisano, was an Italian mathematician.
- 35. The Fibonacci numbers are elements of the sequence 0, 1, 1, 2, 3, 5, 8, 13,
- 36. If we denote the n-th element of the sequence by Fn (n = 0, 1, 2,
- 37. The characteristic equation for this recurrence is It has two roots The general solution of the
- 38. Now we use the initial values for writing the equations for the constants c1 and c2:
- 39. A binary word containing no two consecutive 1’s will be called a sparse word. For example,
- 40. For small n we have: 0 1 2 3 4 Sparse words n Un λ 0
- 41. What is U5 ? If α is a sparse word of length 5 and the first
- 42. If the first letter in α is 1 then the second letter must be 0 and
- 43. In general case let α be a sparse word of the length n. If the first
- 45. Скачать презентацию








































 Показательные уравнения
Показательные уравнения Арксинус. Решение уравнений вида arcsin t=a
Арксинус. Решение уравнений вида arcsin t=a Конспект урока по математике для 1 класса, тема: Дециметр, программа - Перспектива
Конспект урока по математике для 1 класса, тема: Дециметр, программа - Перспектива Перпендикулярные и параллельные прямые
Перпендикулярные и параллельные прямые Презентация и конспект к уроку во 2 классе по теме: Длина ломанной. Периметр многоугольника А.Милн Винни – Пух и его друзья составлен по программе Школа 2000. автор Л.Г.Петресон. Урок предусматривает закрепления и уточнение
Презентация и конспект к уроку во 2 классе по теме: Длина ломанной. Периметр многоугольника А.Милн Винни – Пух и его друзья составлен по программе Школа 2000. автор Л.Г.Петресон. Урок предусматривает закрепления и уточнение Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной Нахождение числа по его дроби. 6 класс
Нахождение числа по его дроби. 6 класс Пирамида. Её элементы. Правильная пирамида. Усечённая пирамида
Пирамида. Её элементы. Правильная пирамида. Усечённая пирамида Логарифмы на ЕГЭ
Логарифмы на ЕГЭ Теорема о площади треугольника
Теорема о площади треугольника Решение нестандартных задач по математике
Решение нестандартных задач по математике Устный счет
Устный счет Свойства последовательности. Функция
Свойства последовательности. Функция Математика. 1 класс. Урок 40. Слагаемое. Сумма - Презентация
Математика. 1 класс. Урок 40. Слагаемое. Сумма - Презентация Обчислення виду 18 – 5. Складання за малюнком задачі на знаходження суми та задачі на різницеве порівняння. Урок №82
Обчислення виду 18 – 5. Складання за малюнком задачі на знаходження суми та задачі на різницеве порівняння. Урок №82 Космос и математика
Космос и математика Планирование эксперимента при поиске оптимальных условий
Планирование эксперимента при поиске оптимальных условий Векторы в пространстве. Операции над векторами
Векторы в пространстве. Операции над векторами Выпуклый анализ. Выпуклые функции.. Лекция 12
Выпуклый анализ. Выпуклые функции.. Лекция 12 Пример решения транспортной задачи (открытая модель)
Пример решения транспортной задачи (открытая модель)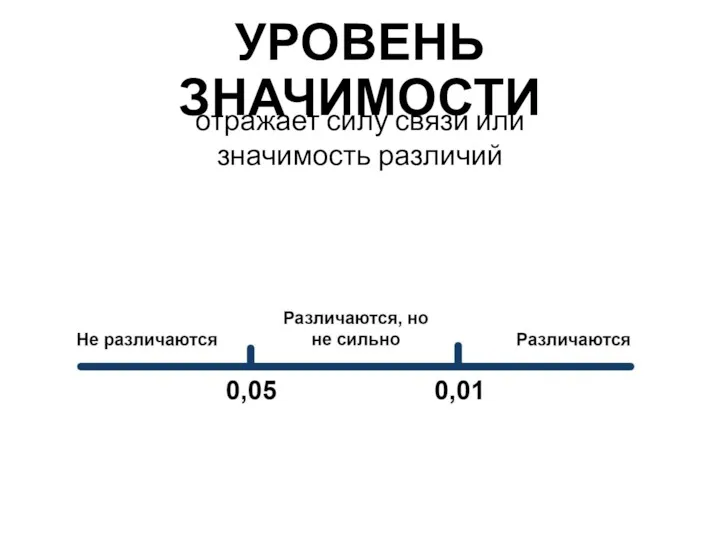 Уровень значимости
Уровень значимости Приёмы табличного вычитания однозначных чисел с переходом через десяток
Приёмы табличного вычитания однозначных чисел с переходом через десяток Математическая игра-викторина Своя игра для 6-7 классов
Математическая игра-викторина Своя игра для 6-7 классов Комплексные числа. Алгебраическая форма комплексного числа
Комплексные числа. Алгебраическая форма комплексного числа Сумма углов треугольника. Лаборатория экспериментов
Сумма углов треугольника. Лаборатория экспериментов Добавь до 10
Добавь до 10 Урок математики Школа России 4 класс
Урок математики Школа России 4 класс Структура задачи
Структура задачи