Содержание
- 2. План: 1. Абсолютные показатели вариации. 2. Относительные показатели вариации. 3. Понятие, виды и свойства дисперсий. 4.
- 3. ПОКАЗАТЕЛИ ВАРИАЦИИ ПРИЗНАКОВ Различия индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Выделяют три формы
- 4. АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ Размах вариации – разность между наибольшим и наименьшим значениями варьирующего признака, показывает, в
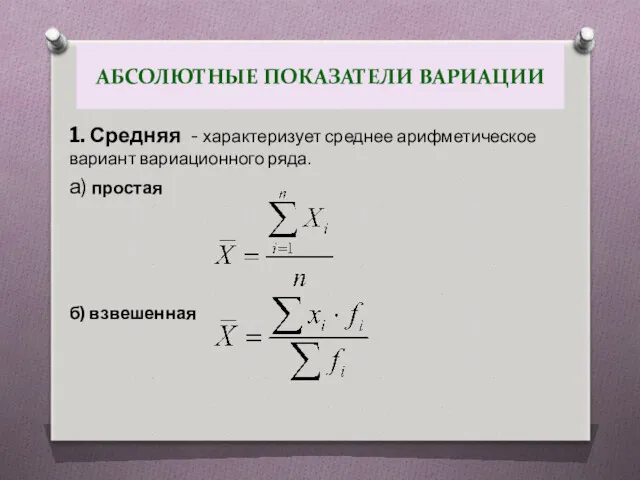
- 5. 1. Средняя - характеризует среднее арифметическое вариант вариационного ряда. а) простая б) взвешенная АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ
- 6. АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины и
- 7. АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ Среднее квадратическое отклонение (нормированное или стандартизированное отклонение) рассчитывается как корень квадратный из дисперсии.
- 8. АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ Среднее линейное отклонение – средняя арифметическая из абсолютных значений отклонений вариант признака от
- 9. ОТНОСИТЕЛЬНЫЕ ПОКАЗАТЕЛИ ВАРИАЦИИ Коэффициент осцилляции – процентное отношение размаха вариации к средней величине признака. Линейный коэффициент
- 10. ПОНЯТИЕ, ВИДЫ И СВОЙСТВА ДИСПЕРСИЙ Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех
- 11. ПОНЯТИЕ, ВИДЫ И СВОЙСТВА ДИСПЕРСИЙ Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящей под влиянием
- 12. Методы расчета сводных характеристик выборки Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде
- 13. Методы расчета сводных характеристик выборки Условными называют варианты, определяемые равенством: где С—ложный нуль (новое начало отсчета);
- 14. Методы расчета сводных характеристик выборки Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант
- 15. Условные варианты. Замечания В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если
- 16. Условные варианты. Пример. Найти условные варианты статистического распределения:
- 17. Условные варианты. Решение Выберем в качестве ложного нуля варианту 33,6 (эта варианта расположена в середине вариационного
- 18. Условные варианты. Решение Найдем условную варианту: Аналогично получим: и2= -1, и3 = 0, и4 =1, и5=2.
- 19. Эмпирические моменты Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами. Эмпирические моменты вычисляют по данным
- 20. Обычные, начальные и центральные эмпирические моменты Обычным эмпирическим моментом порядка k называют величину:
- 21. Обычные, начальные и центральные эмпирические моменты Начальным эмпирическим моментом порядка k называют обычный момент порядка k
- 22. Обычные, начальные и центральные эмпирические моменты В частности, т.е. начальный эмпирический момент первого порядка равен выборочной
- 23. Обычные, начальные и центральные эмпирические моменты Центральным эмпирическим моментом порядка k называют обычный момент порядка k
- 24. Обычные, начальные и центральные эмпирические моменты В частности, т.е. центральный эмпирический момент второго порядка равен выборочной
- 25. Асимметрия и эксцесс Для оценки отклонения эмпирического распределения от нормального используются асимметрия и эксцесс эмпирического распределения:
- 26. Эмпирические и выравнивающие теоретические частоты
- 27. Эмпирические и выравнивающие теоретические частоты
- 28. Эмпирические и выравнивающие теоретические частоты Для непрерывного случая в случае, если случайная величина Х подчиняется стандартному
- 29. Построение гипотетической нормальной кривой
- 30. Согласие теоретического и статистического распределения Если между теоретической кривой распределения F(X) и эмпирической функцией распределения существуют
- 31. Критерий согласия Пирсона Как бы точно не вычислялись теоретические частоты они, как правило, не совпадают с
- 32. Критерий согласия Пирсона
- 33. Сравнение теоретических и эмпирических распределений Нулевая гипотеза. Согласно этой гипотезе первоначально принимается, что между эмпирическим и
- 34. Число степеней свободы – это общее число величин, по которым вычисляются соответствующие статистические показатели, минус число
- 35. Критерий согласия Пирсона
- 37. Скачать презентацию

































 Понятие алгоритма и способы записи алгоритмов. (урок 1)
Понятие алгоритма и способы записи алгоритмов. (урок 1) Действия с натуральными числами
Действия с натуральными числами Путешествие в космос
Путешествие в космос Теорема Пифагора
Теорема Пифагора Нумерація трицифрових чисел
Нумерація трицифрових чисел Десятичные дроби. Математика и экология (часть 1)
Десятичные дроби. Математика и экология (часть 1) Manipulator Kinematics, Link Description, Link Connections
Manipulator Kinematics, Link Description, Link Connections Random variables – discrete random variables. Week 6 (2)
Random variables – discrete random variables. Week 6 (2) Свойства прямоугольника. 2 класс
Свойства прямоугольника. 2 класс Благоприятствующие элементарные события (8 класс)
Благоприятствующие элементарные события (8 класс) Презентации к урокам
Презентации к урокам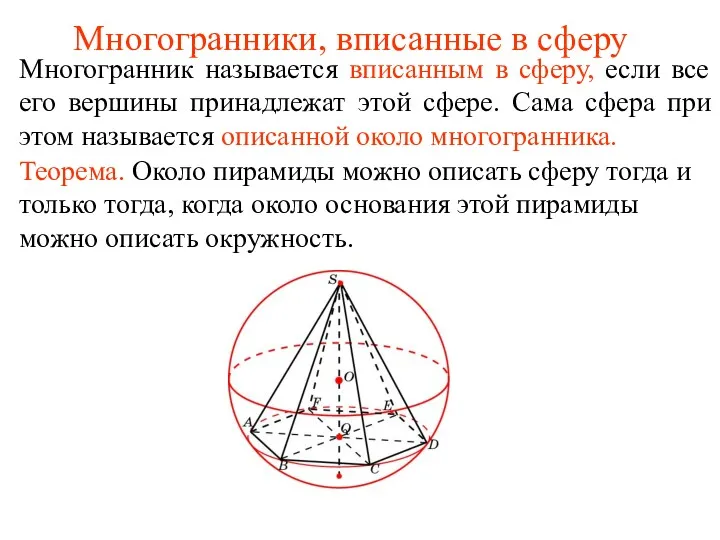 Многогранники, вписанные в сферу
Многогранники, вписанные в сферу Использование современных технологий на уроках математики
Использование современных технологий на уроках математики Тела вращения. Геометрия
Тела вращения. Геометрия Survey. Factors that affecton shopping centers selection
Survey. Factors that affecton shopping centers selection Умножение и деление числа на 3
Умножение и деление числа на 3 Интервальные ряды
Интервальные ряды Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными Интеллектуально познавательная игра Умники и умницы
Интеллектуально познавательная игра Умники и умницы Вычесть число 3.
Вычесть число 3. Векторы. Средняя линия трапеции. Подготовка к контрольной работе
Векторы. Средняя линия трапеции. Подготовка к контрольной работе Формулы приведения
Формулы приведения Призма
Призма Линейная функция и её график
Линейная функция и её график Урок математики в 4 классе (Л.Занков) по теме Округление чисел
Урок математики в 4 классе (Л.Занков) по теме Округление чисел Презентация к уроку математики 4 класс. УМК Школа России
Презентация к уроку математики 4 класс. УМК Школа России Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс