Содержание
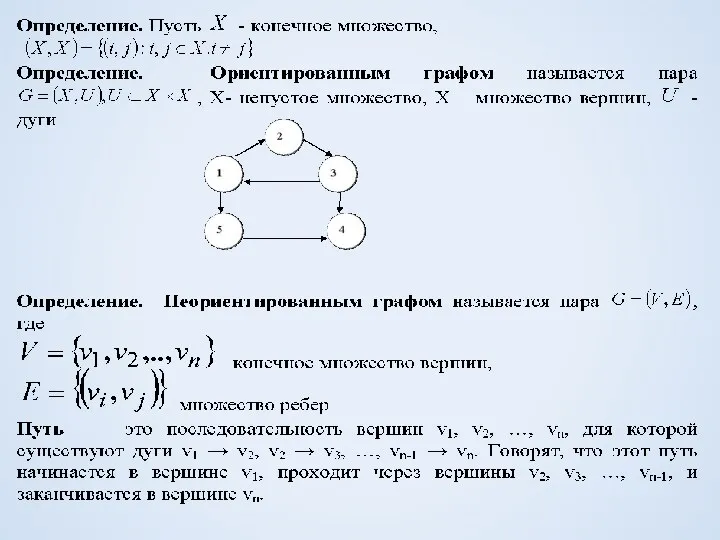
- 4. Путь называется: простым, если ни одна вершина не встречается более одного раза замкнутым, если vt+1 =
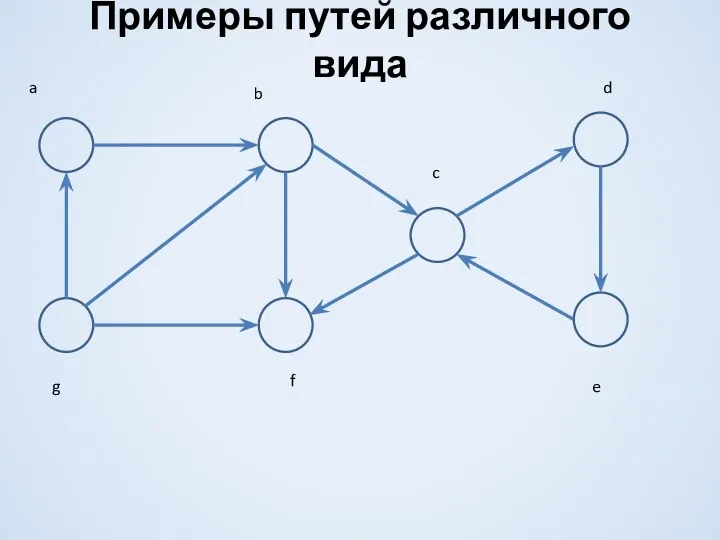
- 5. Примеры путей различного вида a b c d e g f
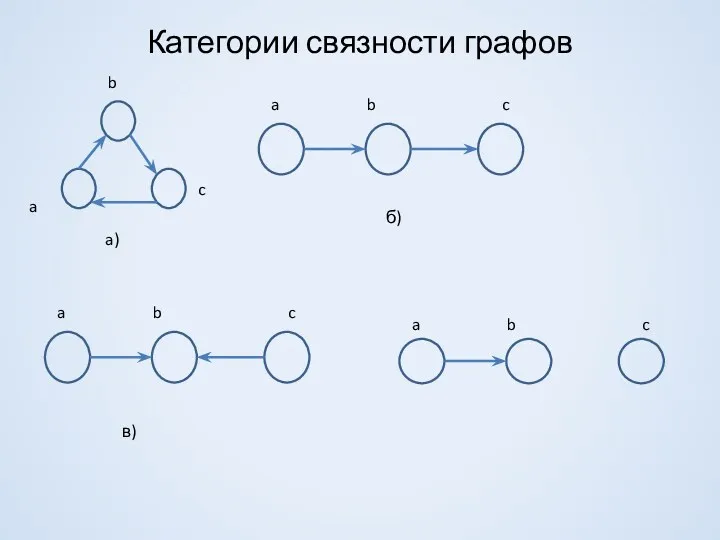
- 7. Категории связности графов a b c a) б) в)
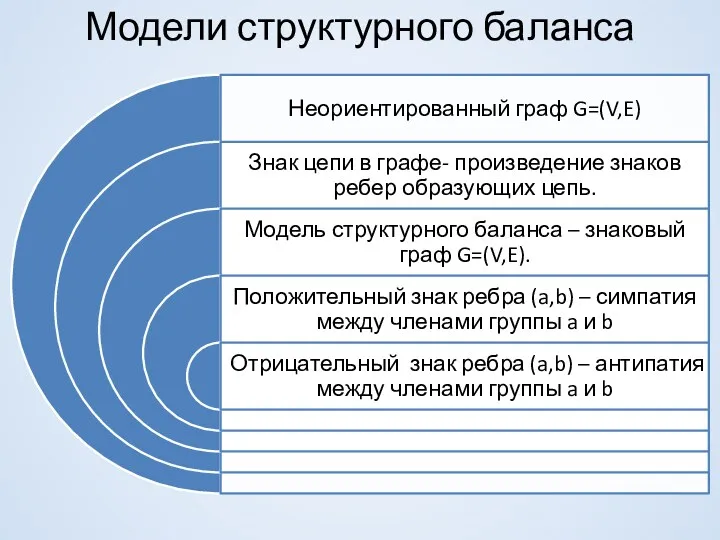
- 9. Модели структурного баланса
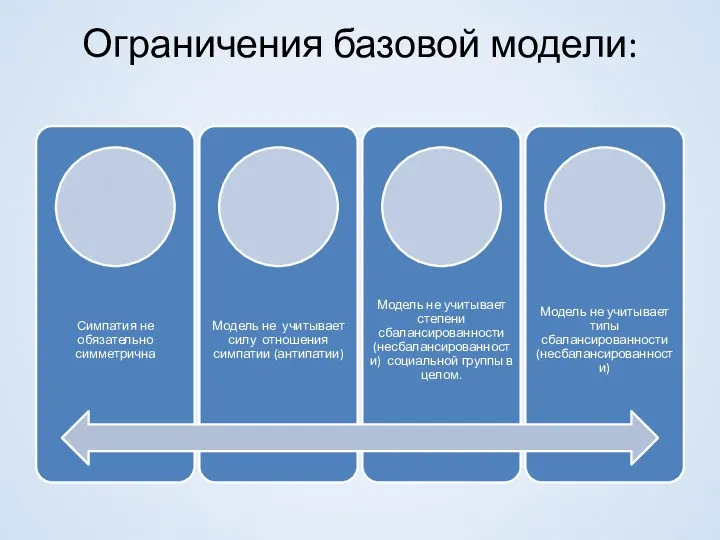
- 10. Ограничения базовой модели:
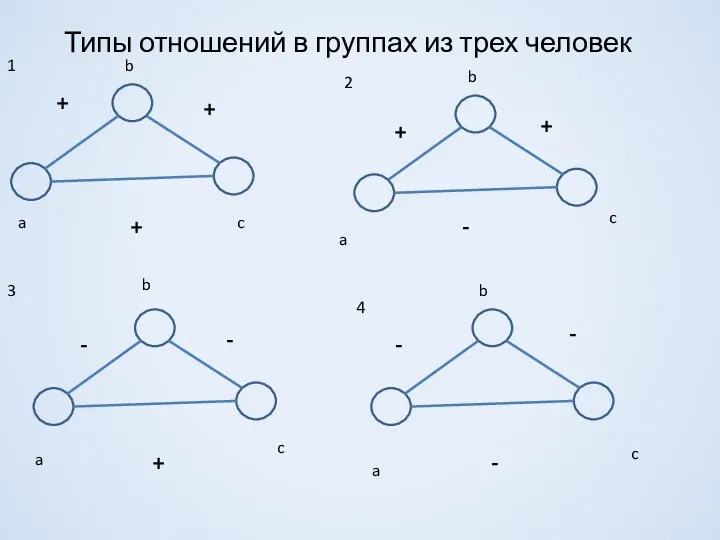
- 11. Типы отношений в группах из трех человек + + + + + - - - -
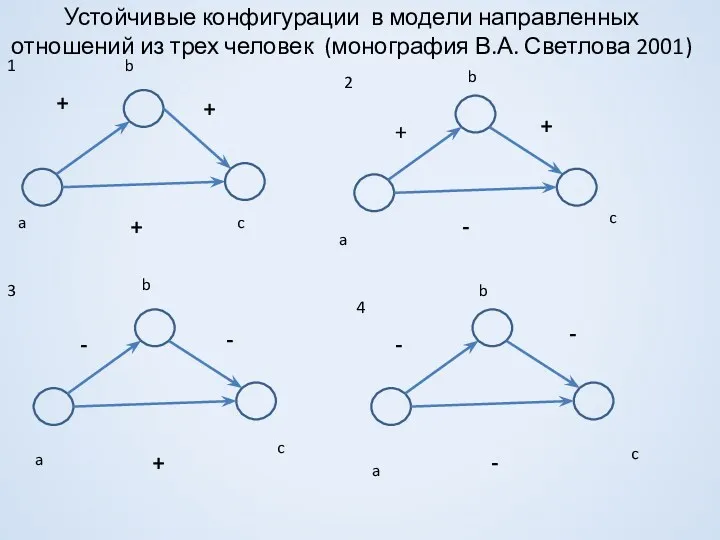
- 12. Устойчивые конфигурации в модели направленных отношений из трех человек (монография В.А. Светлова 2001) + + +
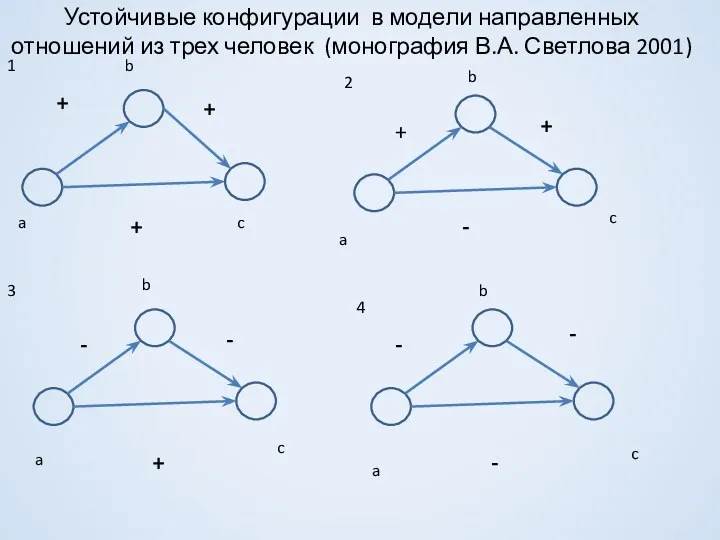
- 15. Устойчивые конфигурации в модели направленных отношений из трех человек (монография В.А. Светлова 2001) + + +
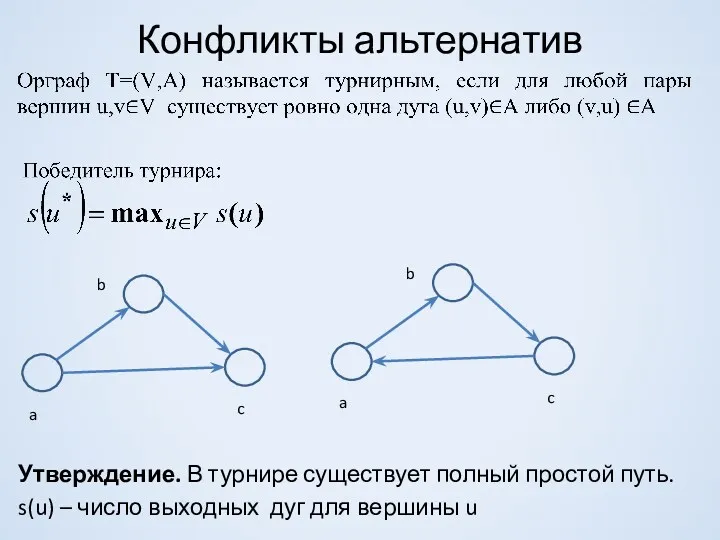
- 16. Конфликты альтернатив Утверждение. В турнире существует полный простой путь. s(u) – число выходных дуг для вершины
- 17. Статусные конфликты Математическая модель – связный бесконтурный орграф D=(V,A) Дуга (u,v) Путь от u до v
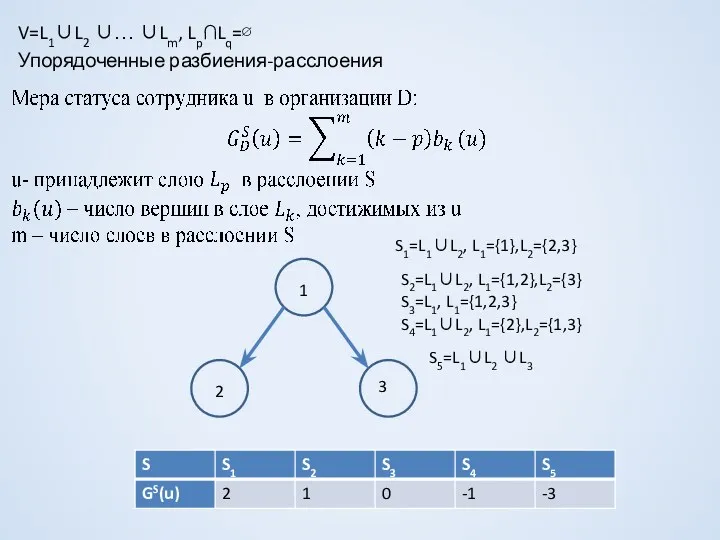
- 18. V=L1∪L2 ∪… ∪Lm, Lp∩Lq=∅ Упорядоченные разбиения-расслоения S1=L1∪L2, L1={1},L2={2,3} S2=L1∪L2, L1={1,2},L2={3} S3=L1, L1={1,2,3} S4=L1∪L2, L1={2},L2={1,3} S5=L1∪L2 ∪L3
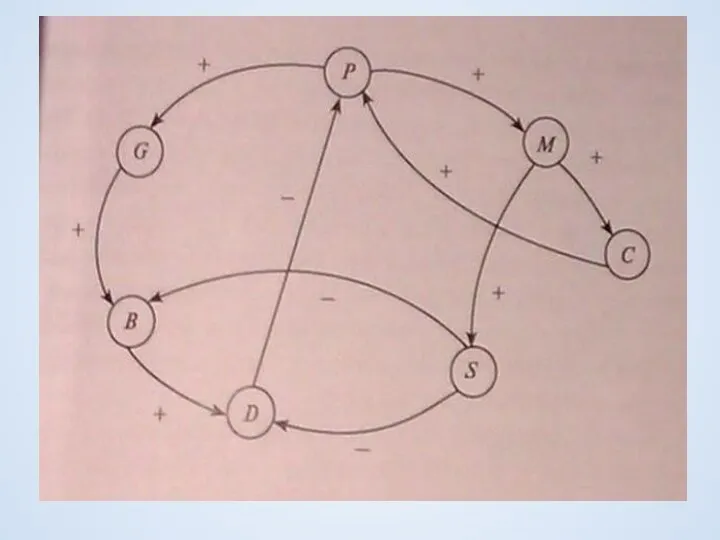
- 19. Когнитивные карты конфликтных процессов
- 21. Пример P- численность городского населения G-количество мусора на единицу площади B – бактериологическая зараженность на единицу
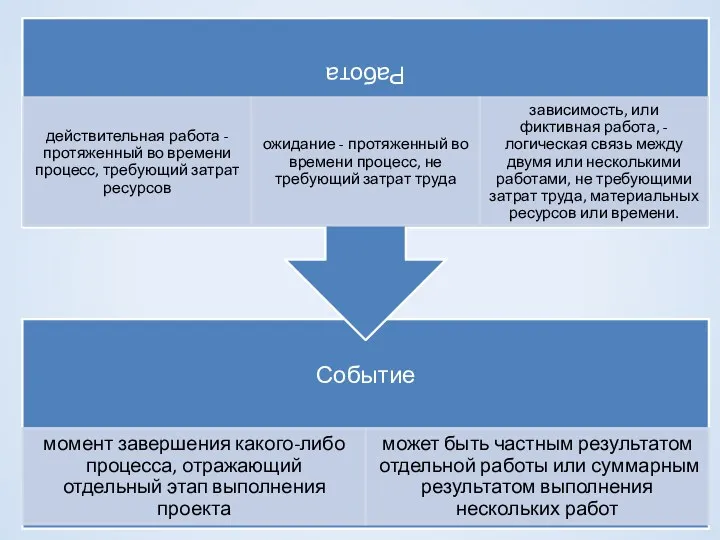
- 23. Сетевое планирование и управление
- 27. Общие черты и особенности проектов
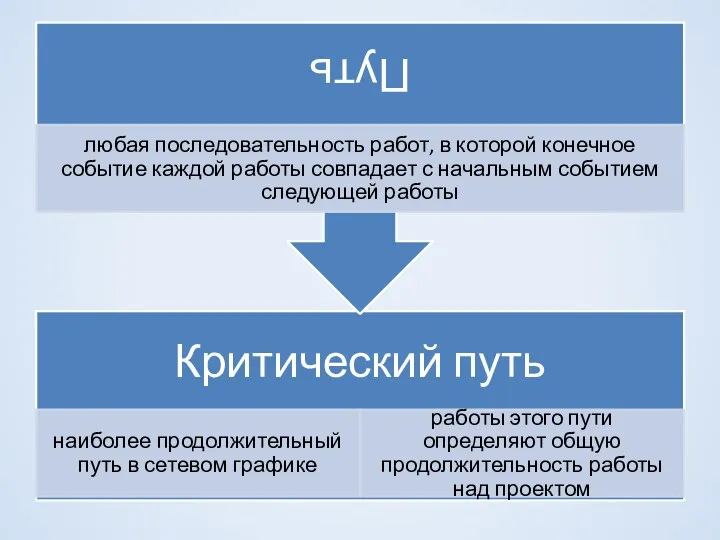
- 29. Метод критического пути
- 32. Поиск нового критического пути Работа (k,l) Узел с номером k принадлежит новому критическому пути Если узел
- 33. Оптимизация плана комплекса работ
- 35. Скачать презентацию


















 Связь между бесконечно малыми и бесконечно большими величинами
Связь между бесконечно малыми и бесконечно большими величинами Сфера и шар
Сфера и шар Презентация к уроку математики в 4 классе Задачи на движение
Презентация к уроку математики в 4 классе Задачи на движение Геометрический смысл производной
Геометрический смысл производной Интерактивный тренажёр Сложение и вычитание чисел в пределах 100
Интерактивный тренажёр Сложение и вычитание чисел в пределах 100 Модуль числа (часть 1)
Модуль числа (часть 1) Система обобщающего повторения на уроках геометрии при подготовке к ГИА
Система обобщающего повторения на уроках геометрии при подготовке к ГИА График функции
График функции Аксонометрия
Аксонометрия Математика. Раздел 7. Функции и графики
Математика. Раздел 7. Функции и графики Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Задачи на нахождение процентов
Задачи на нахождение процентов Гномы 2(математические тренинги)
Гномы 2(математические тренинги) Алгоритм сложения трёхзначных чисел.
Алгоритм сложения трёхзначных чисел. Решение квадратных неравенств. 8 класс
Решение квадратных неравенств. 8 класс Алгоритми і виконавці
Алгоритми і виконавці Решение квадратных уравнений по формуле. 8 класс
Решение квадратных уравнений по формуле. 8 класс Основы математической обработки информации
Основы математической обработки информации Задача по финансовой математике
Задача по финансовой математике Принцип Дирихле
Принцип Дирихле Сложения и вычитания десятичных дробей
Сложения и вычитания десятичных дробей Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Формирование понятия об арифметических действиях и их свойствах в начальной школе
Формирование понятия об арифметических действиях и их свойствах в начальной школе Задачи на построение. 7 класс
Задачи на построение. 7 класс вероятность с теорией
вероятность с теорией Банк мультимедийных презентаций по ФЭМП
Банк мультимедийных презентаций по ФЭМП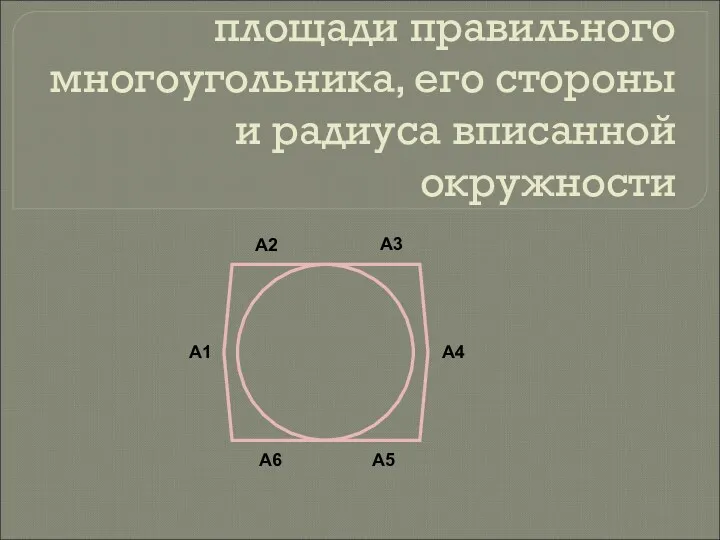 Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Делители и кратные. 5 класс
Делители и кратные. 5 класс