Содержание
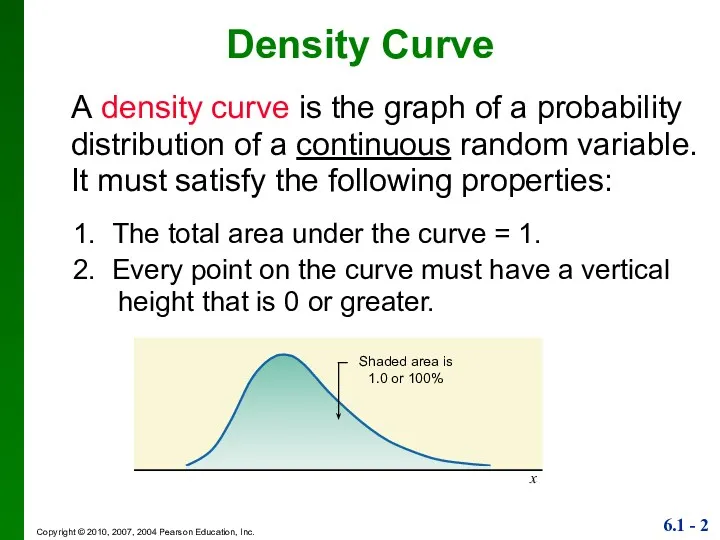
- 2. A density curve is the graph of a probability distribution of a continuous random variable. It
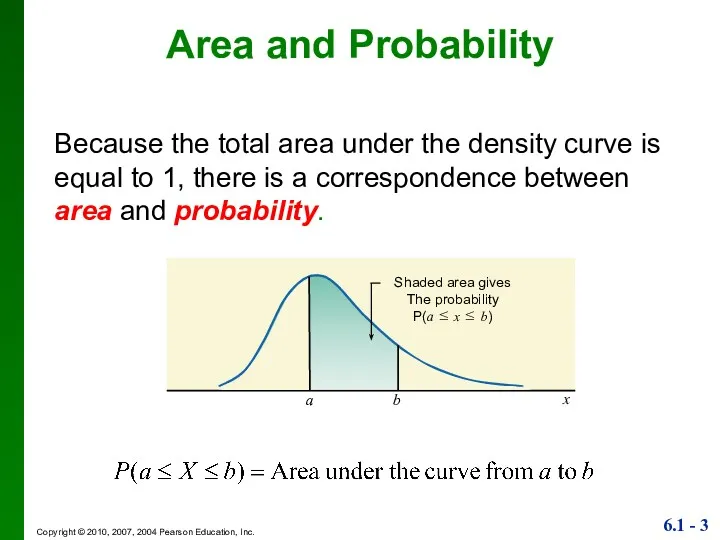
- 3. Because the total area under the density curve is equal to 1, there is a correspondence
- 4. Uniform Distribution (Definition) A continuous random variable has a uniform distribution if its values are spread
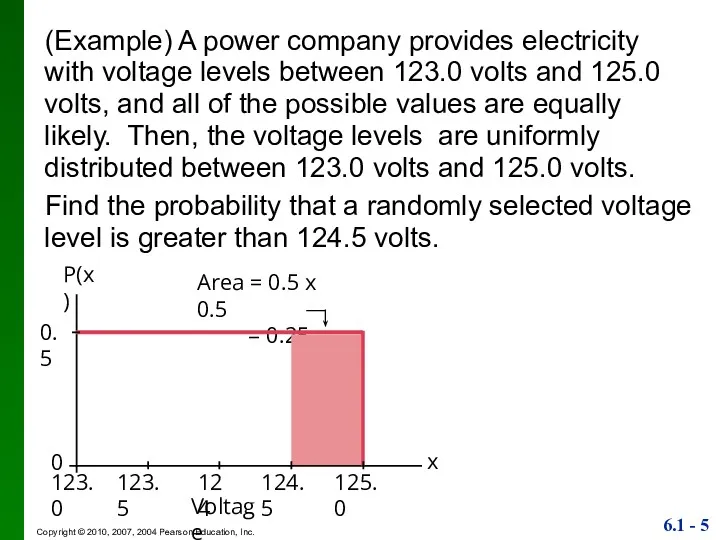
- 5. (Example) A power company provides electricity with voltage levels between 123.0 volts and 125.0 volts, and
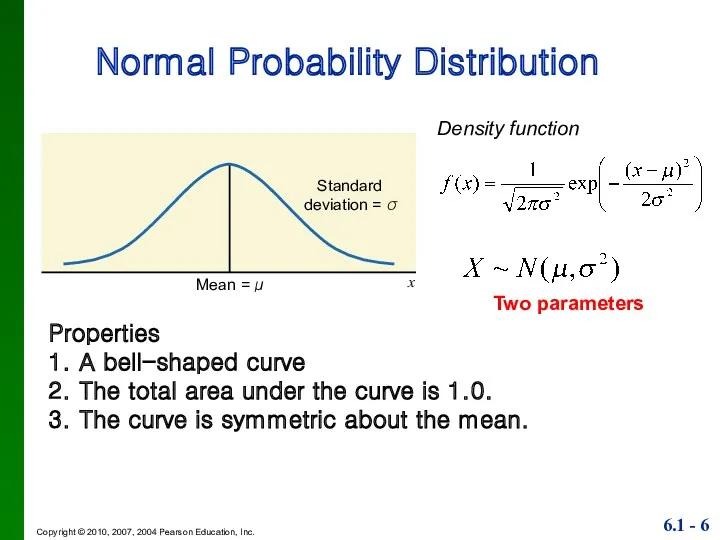
- 6. Normal Probability Distribution Properties 1. A bell-shaped curve 2. The total area under the curve is
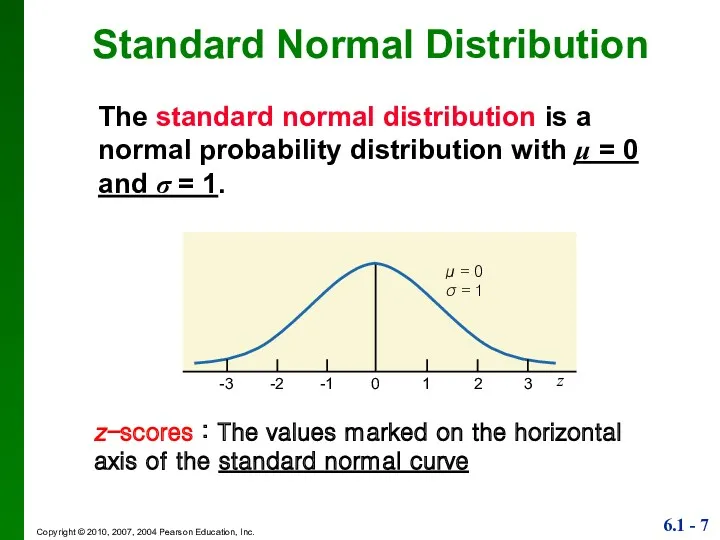
- 7. Standard Normal Distribution The standard normal distribution is a normal probability distribution with μ = 0
- 8. P(a P(Z > a) = probability that the z-score is greater than a. P(Z Finding probability
- 9. R for normal distribution dnorm(x, mean = 0, sd = 1) =density function, not P(X=0) pnorm(x,
- 10. Example Required area
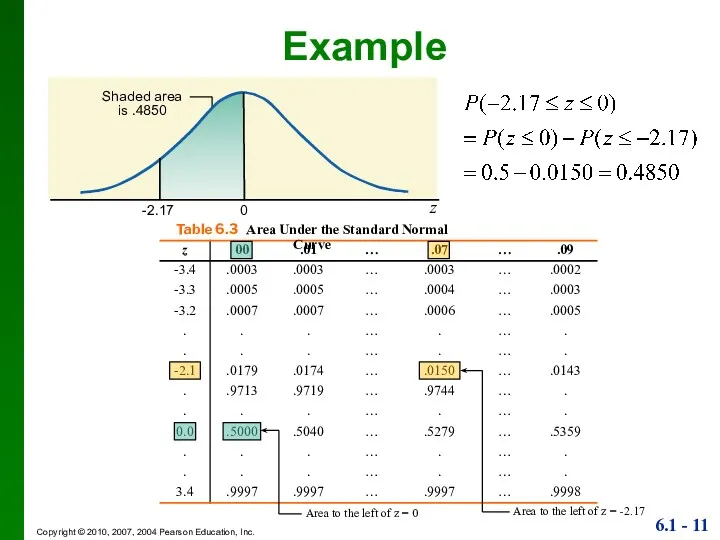
- 11. Example z Shaded area is .4850 -2.17 0 Table 6.3 Area Under the Standard Normal Curve
- 12. Assume that the readings of a thermometer are normally distributed with the mean 0ºC and the
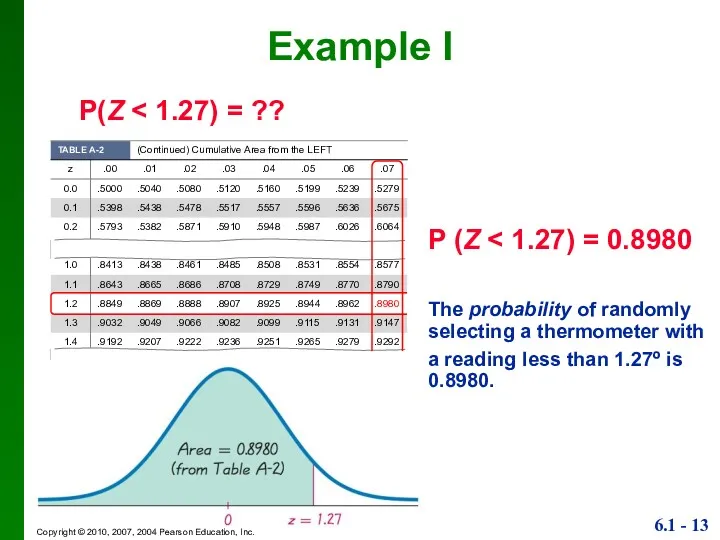
- 13. P(Z Example I P (Z The probability of randomly selecting a thermometer with a reading less
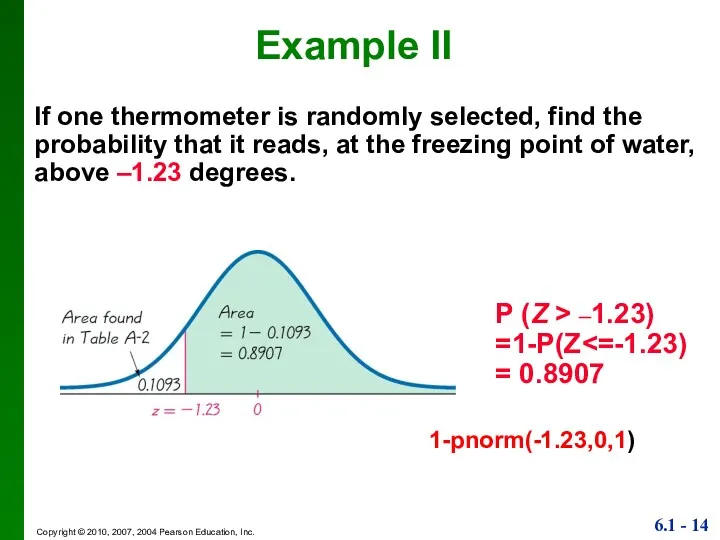
- 14. If one thermometer is randomly selected, find the probability that it reads, at the freezing point
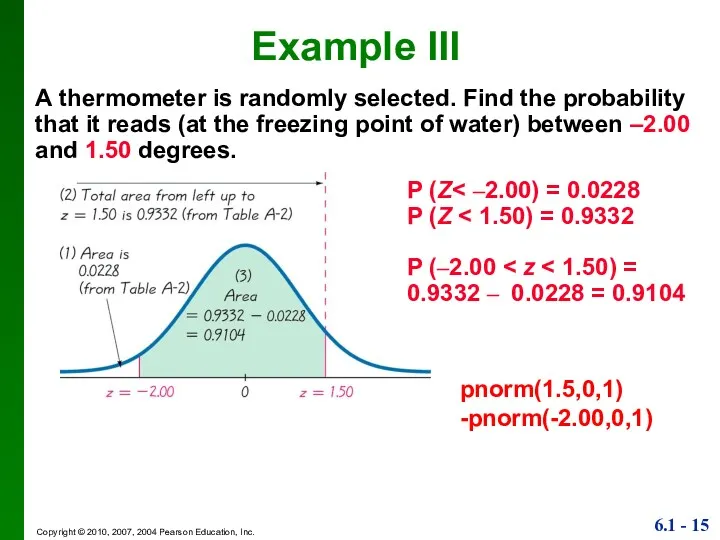
- 15. A thermometer is randomly selected. Find the probability that it reads (at the freezing point of
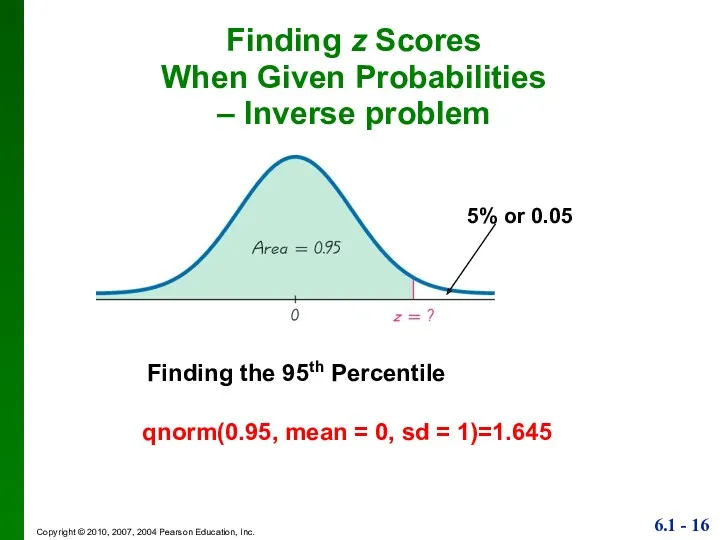
- 16. Finding z Scores When Given Probabilities – Inverse problem Finding the 95th Percentile 5% or 0.05
- 17. Applications of Normal Distributions
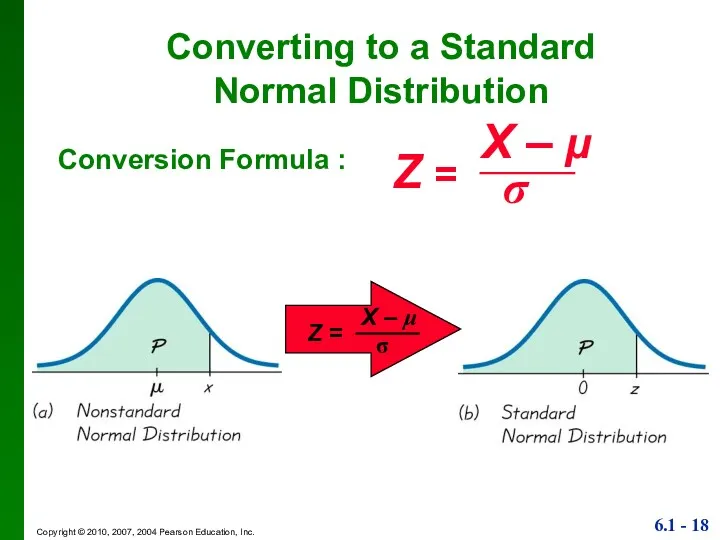
- 18. Converting to a Standard Normal Distribution Conversion Formula :
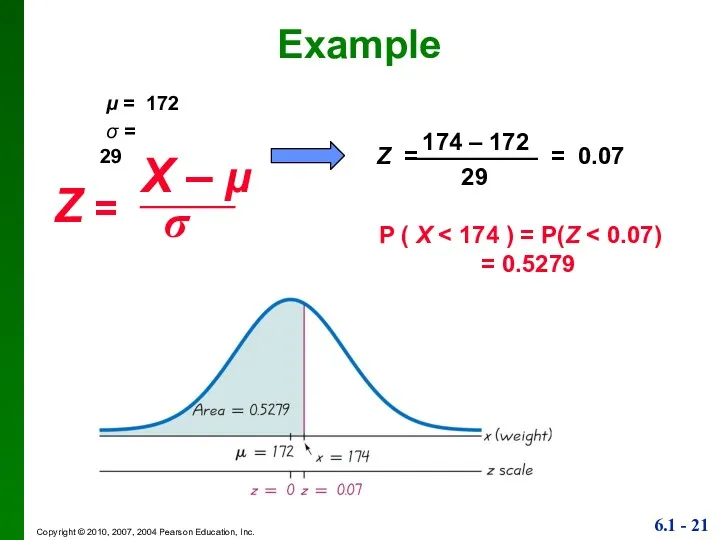
- 20. Example Find P ( X Use Suppose X ~ N(μ , σ2), μ = 172, σ
- 21. Example P ( X = 0.5279
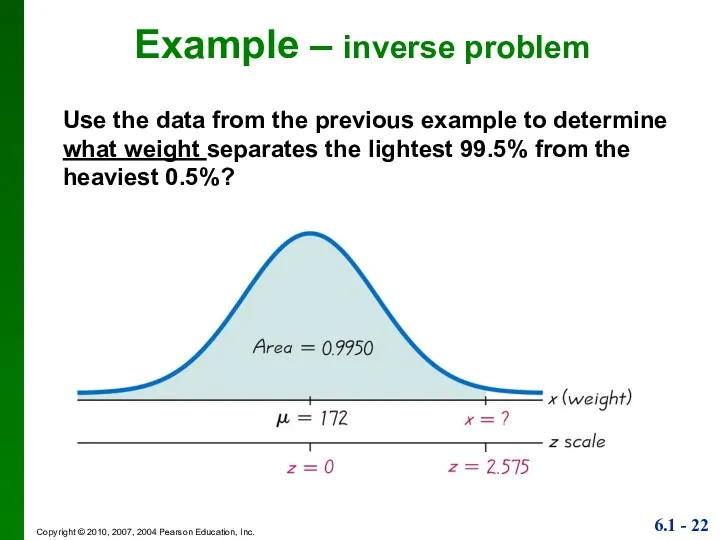
- 22. Example – inverse problem Use the data from the previous example to determine what weight separates
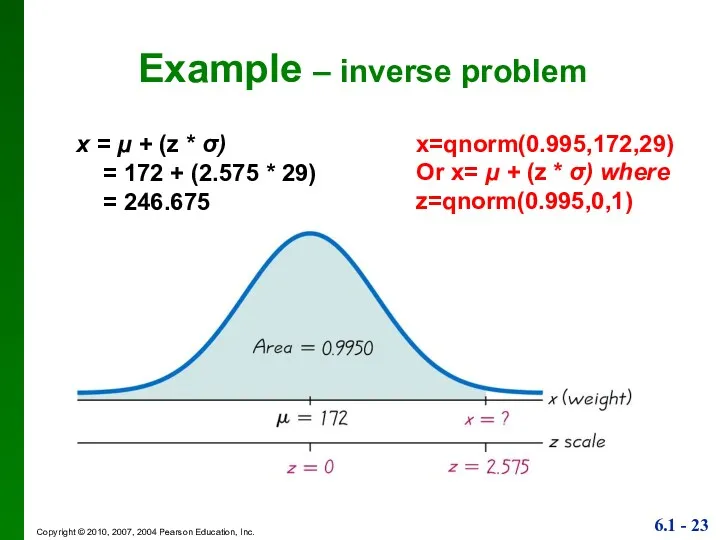
- 23. x = μ + (z * σ) = 172 + (2.575 * 29) = 246.675 Example
- 24. Sum of Independent Normal Random Variables Let and are independent and normally distributed with means and
- 25. The Central Limit Theorem
- 26. Key Concept The Central Limit Theorem tells us that for a population with any distribution, the
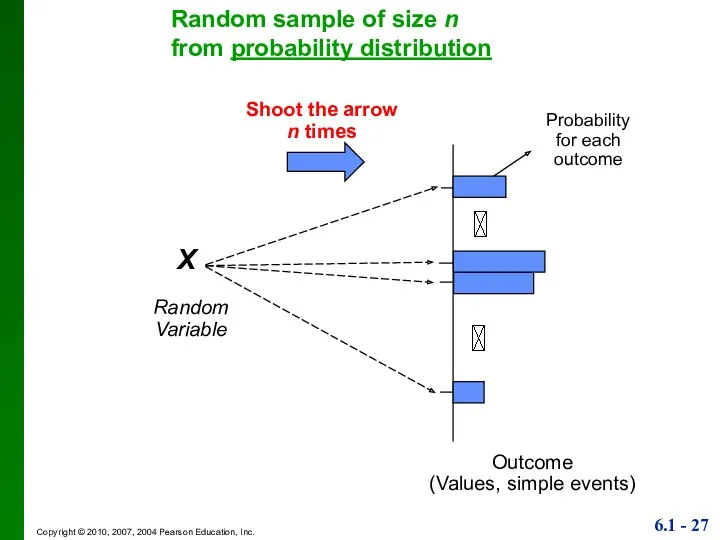
- 27. X Random Variable Shoot the arrow n times Outcome (Values, simple events) Probability for each outcome
- 28. Central Limit Theorem 1. The random variable X has a distribution with mean µ and standard
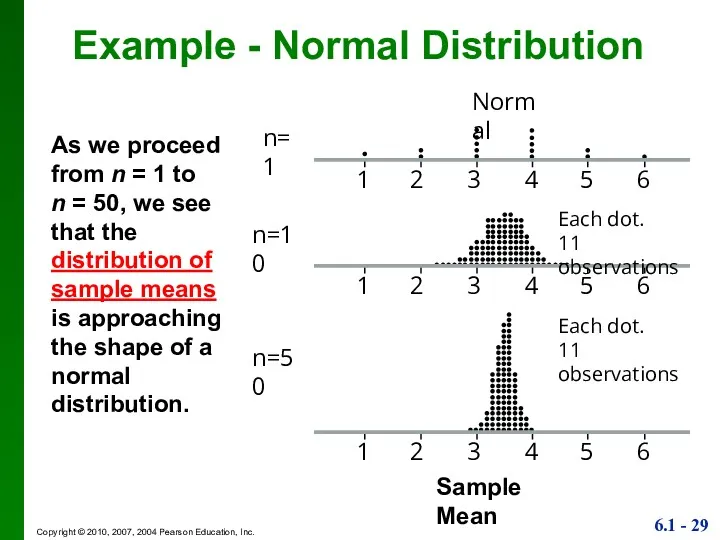
- 29. Example - Normal Distribution As we proceed from n = 1 to n = 50, we
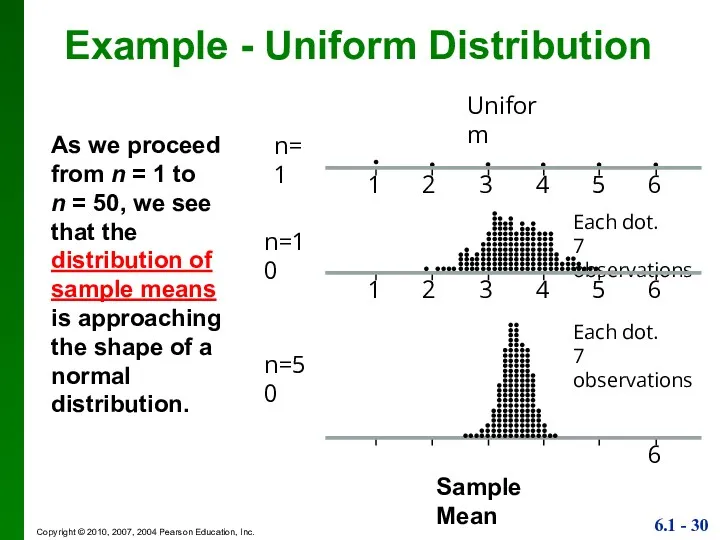
- 30. Example - Uniform Distribution As we proceed from n = 1 to n = 50, we
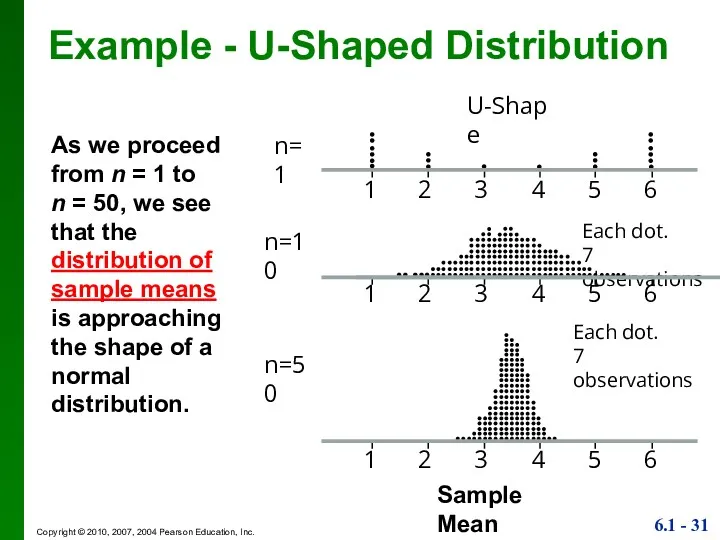
- 31. Example - U-Shaped Distribution As we proceed from n = 1 to n = 50, we
- 32. Notation the mean of the sample mean the standard deviation of sample mean Show them !
- 33. Informal: Whatever the population, the distribution of is normal with mean and standard deviation when n
- 34. Practical Rules Commonly Used (Case 1) The original population is normally distributed. For any sample size
- 35. Assume the population of weights of men is normally distributed with a mean of 172 lb
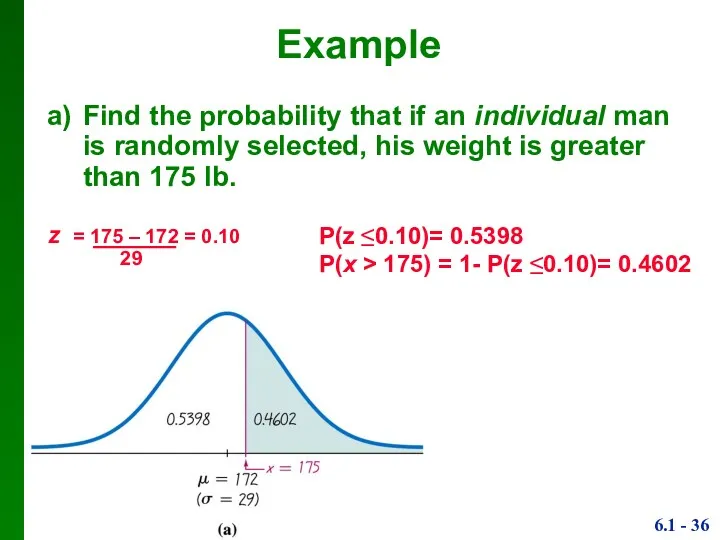
- 36. a) Find the probability that if an individual man is randomly selected, his weight is greater
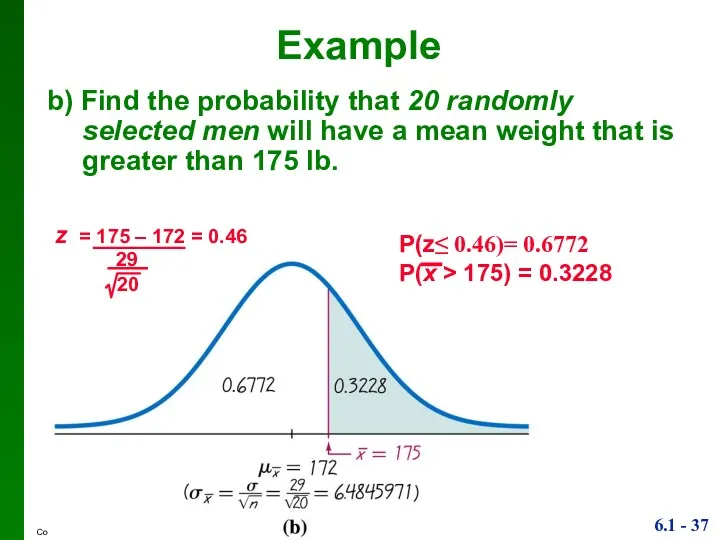
- 37. b) Find the probability that 20 randomly selected men will have a mean weight that is
- 38. Assume the population of weights of men has a mean of 172 lb and a standard
- 39. Normal as Approximation to Binomial
- 40. Review Binomial Probability Distribution 1. The procedure must have a fixed number of trials. 2. The
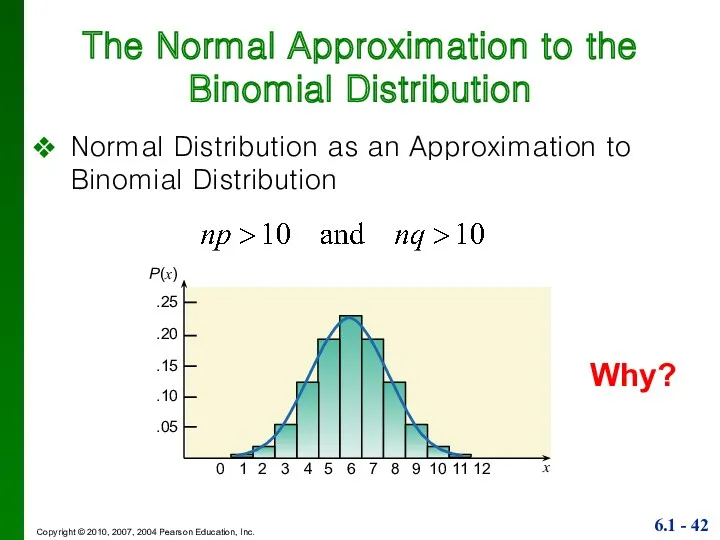
- 41. Approximation of a Binomial Distribution with a Normal Distribution np ≥ 10 nq ≥ 10
- 42. The Normal Approximation to the Binomial Distribution Normal Distribution as an Approximation to Binomial Distribution .25
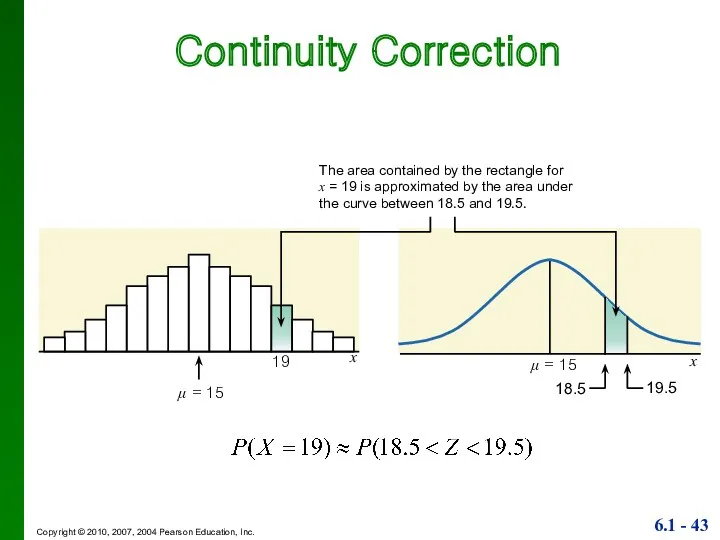
- 43. Continuity Correction x 18.5 19 μ = 15 x The area contained by the rectangle for
- 44. Procedure for Using a Normal Distribution to Approximate a Binomial Distribution 1. Check that np ≥
- 45. 4. Draw a normal distribution centered about μ, then draw a vertical strip area centered over
- 46. Suppose there are 213 passengers in a train and the probability that a passenger is male
- 47. Suppose there are 213 passengers in a train and the probability that a passenger is male
- 49. Скачать презентацию






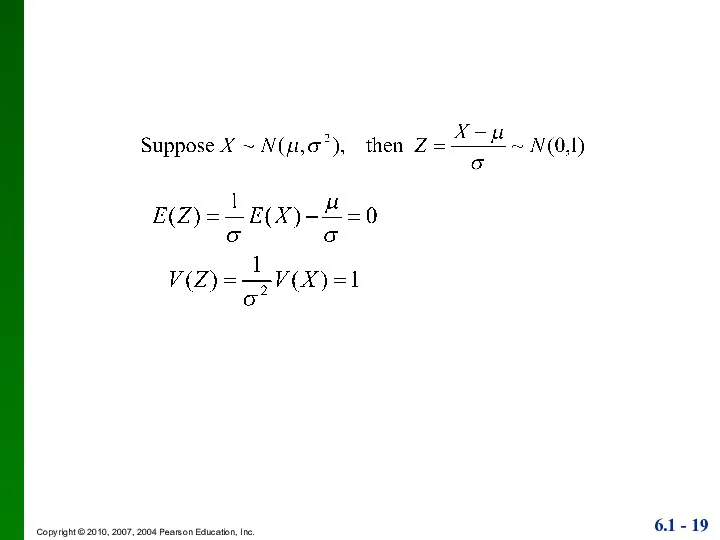

















 Линейная функция. Алгебра, 7 класс
Линейная функция. Алгебра, 7 класс Десятичные дроби. Задания для устного счета
Десятичные дроби. Задания для устного счета Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Параллелепипед и куб
Параллелепипед и куб Предел функции. Непрерывность функции. Точки разрыва
Предел функции. Непрерывность функции. Точки разрыва Решение задач с процентами: нахождение числа по процентам. 5 класс
Решение задач с процентами: нахождение числа по процентам. 5 класс Алгебраическая сумма и её свойства
Алгебраическая сумма и её свойства Красота в математике или применение векторов к доказательству стереометрических теорем
Красота в математике или применение векторов к доказательству стереометрических теорем Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Презентация к уроку Прибавление чисел 7, 8. 9
Презентация к уроку Прибавление чисел 7, 8. 9 Точность коэффициентов множественной регрессии
Точность коэффициентов множественной регрессии Регрессионный анализ
Регрессионный анализ Случаи сложения вида +4
Случаи сложения вида +4 КВН по математике
КВН по математике Десятичные дроби. Повторение. Действия с десятичными дробями
Десятичные дроби. Повторение. Действия с десятичными дробями ПРЕЗЕНТАЦИЯ ОБЪЕМ
ПРЕЗЕНТАЦИЯ ОБЪЕМ Симметрия в химии
Симметрия в химии Сложение и вычитание чисел
Сложение и вычитание чисел Сходимость знакоположительных рядов
Сходимость знакоположительных рядов Матриці, дії з матрицями. Визначники, їх властивості
Матриці, дії з матрицями. Визначники, їх властивості Формулирование факторов для использования их в статистической модели
Формулирование факторов для использования их в статистической модели Умножение круглых многозначных чисел
Умножение круглых многозначных чисел Подготовка к ЕГЭ. Задача В8
Подготовка к ЕГЭ. Задача В8 Длина окружности. 6 класс:
Длина окружности. 6 класс: Готовимся к ЕГЭ: задачи на проценты
Готовимся к ЕГЭ: задачи на проценты Сложение и вычитание положительных и отрицательных чисел. 6 класс
Сложение и вычитание положительных и отрицательных чисел. 6 класс Среднее арифметическое
Среднее арифметическое Решение задач. 1 класс
Решение задач. 1 класс