Содержание
- 2. Общее уравнение прямой М0(х0; у0 ) Уравнение вида: Теорема с произвольными коэффициентами А; В; С такими
- 3. Общее уравнение прямой Найдем разность уравнений (1) и (2): Пусть точки М0(х0; у0 ) и М
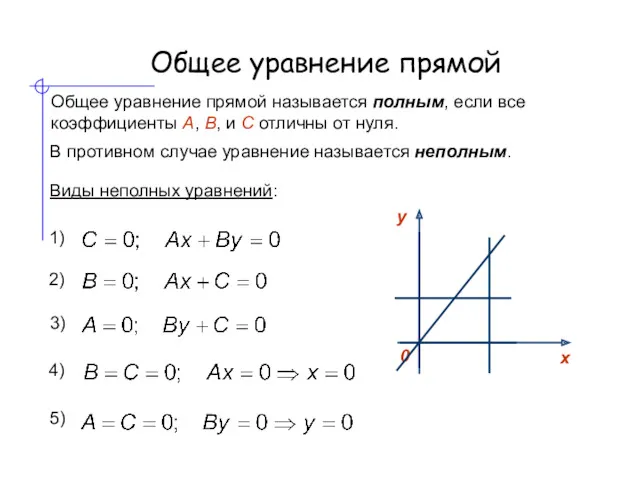
- 4. Общее уравнение прямой Общее уравнение прямой называется полным, если все коэффициенты А, В, и С отличны
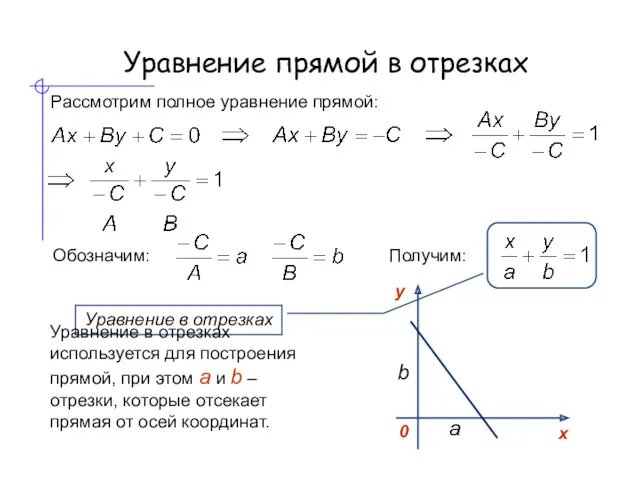
- 5. Уравнение прямой в отрезках Рассмотрим полное уравнение прямой: Обозначим: Получим: Уравнение в отрезках b a Уравнение
- 6. Каноническое уравнение прямой Любой ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Требуется найти
- 7. Каноническое уравнение прямой Пусть прямая проходит через две заданные и отличные друг от друга точки: М1(х1;
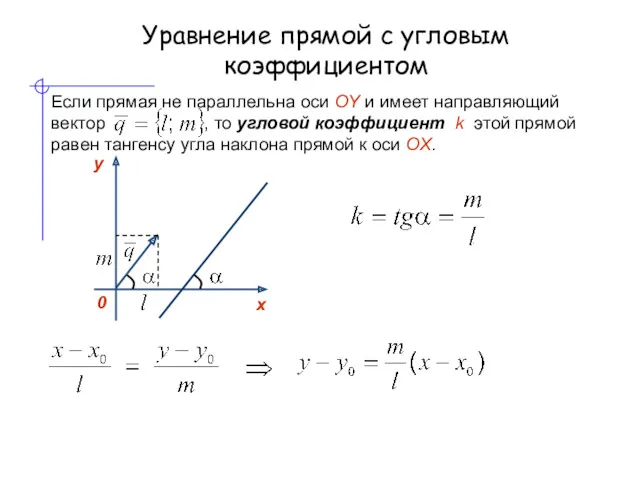
- 8. Уравнение прямой с угловым коэффициентом Уравнение прямой с угловым коэффициентом Уравнение прямой с угловым коэффициентом
- 9. Пример Прямая проходит через точку М(1; 2 ) и имеет направляющий вектор: Написать: каноническое, общее уравнение
- 10. Пример 3. Уравнение в отрезках: 4. Уравнение с угловым коэффициентом: М b a
- 11. Угол между двумя прямыми Пусть две прямые L1 и L2 заданы общими уравнениями: Угол между этими
- 12. Угол между двумя прямыми Пусть две прямые L1 и L2 заданы каноническими уравнениями: Угол между этими
- 13. Угол между двумя прямыми Пусть две прямые L1 и L2 заданы уравнениями с угловыми коэффициентами:
- 14. Расстояние от точки до прямой Пусть необходимо найти расстояние от точки М0(х0; у0 ) до прямой,
- 15. Расстояние от точки до прямой Точка М1(х1; у1 ) принадлежит прямой L , следовательно:
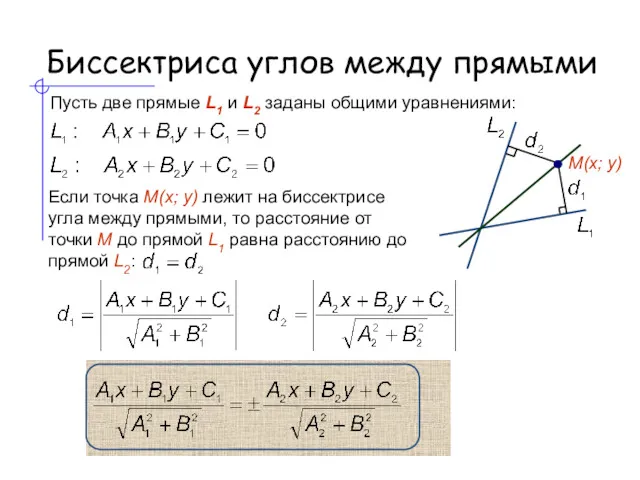
- 16. Биссектриса углов между прямыми Пусть две прямые L1 и L2 заданы общими уравнениями: Если точка M(x;
- 17. Деление отрезка в заданном отношении Разделить отрезок М1М2 в заданном отношении λ > 0 значит найти
- 18. Пример Даны вершины треугольника: А(1; 1); В(10; 13); С(13; 6) Найти: Уравнения высоты, медианы и биссектрисы,
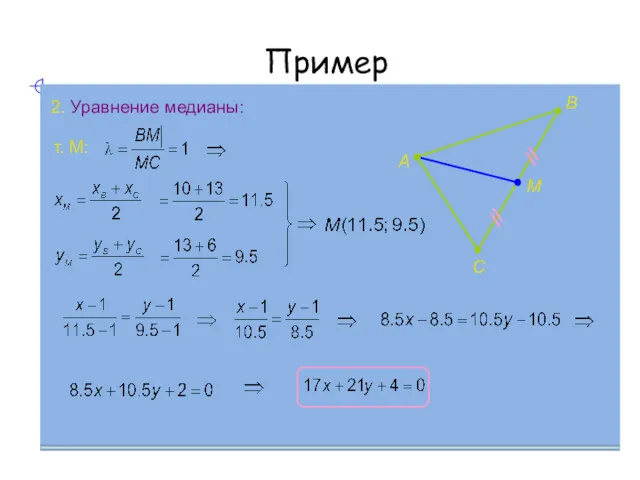
- 19. Пример 2. Уравнение медианы: А В С М т. М:
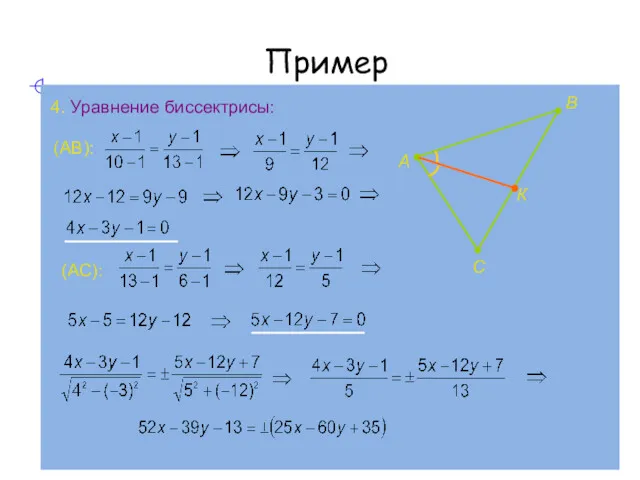
- 20. Пример 4. Уравнение биссектрисы: А В С К (АВ): (АС):
- 22. Скачать презентацию













 Простейшие геометрические фигуры
Простейшие геометрические фигуры Случаи сложения вида +4
Случаи сложения вида +4 Единицы стоимости: рубль, копейка.
Единицы стоимости: рубль, копейка. Повторение умножения многозначных чисел, оканчивающихся нулями
Повторение умножения многозначных чисел, оканчивающихся нулями Правильные многогранники. Геометрия 10 класс
Правильные многогранники. Геометрия 10 класс Методика вивчення рівнянь і нерівностей в основній школі. Методика вивчення систем рівнянь і нерівностей
Методика вивчення рівнянь і нерівностей в основній школі. Методика вивчення систем рівнянь і нерівностей Нормальное распределение
Нормальное распределение Презентация раздела математики Величины УМК Школа России 4 класс
Презентация раздела математики Величины УМК Школа России 4 класс Тетраэдр. Параллелепипед. Задачи на построение сечений
Тетраэдр. Параллелепипед. Задачи на построение сечений Сложение УМК Школа 2100
Сложение УМК Школа 2100 Координатная прямая
Координатная прямая Деление с остатком (заключительный урок). 3 класс.( 8 ноября 2015 год)
Деление с остатком (заключительный урок). 3 класс.( 8 ноября 2015 год) ОГЭ 2018. Модуль Геометрия
ОГЭ 2018. Модуль Геометрия Использование блоков Дьёнеша с целью развития логико – математических представлений у детей дошкольного возраста.
Использование блоков Дьёнеша с целью развития логико – математических представлений у детей дошкольного возраста. Сложение векторов
Сложение векторов Аксиоматический метод в геометрии
Аксиоматический метод в геометрии Модуль Алгебра 8 класс
Модуль Алгебра 8 класс Симметрия в природе
Симметрия в природе Закон больших чисел. Предельные теоремы
Закон больших чисел. Предельные теоремы Умножение и деление десятичных дробей на натуральные числа
Умножение и деление десятичных дробей на натуральные числа Сложение и вычитание чисел
Сложение и вычитание чисел Преобразования фигур. Движение. Уроки геометрии в 8 классе
Преобразования фигур. Движение. Уроки геометрии в 8 классе Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график 3 класс урок математики Закрепление Диск
3 класс урок математики Закрепление Диск Понятие объема тела
Понятие объема тела Основы теории вероятностей
Основы теории вероятностей Обобщение темы Окружность, круг.
Обобщение темы Окружность, круг. Системы уравнений с двумя переменными
Системы уравнений с двумя переменными