Содержание
- 2. СОДЕРЖАНИЕ: Часть 1. Общие черты методов типа ветвей и границ. Часть 2. Методы типа ветвей и
- 3. ЧАСТЬ 1: МЕТОДЫ ТИПА ВЕТВЕЙ И ГРАНИЦ Две обязательные компоненты методов типа ветвей и границ: Построение
- 4. ИДЕЯ МЕТОДОВ ТИПА ВЕТВЕЙ И ГРАНИЦ Все множество планов решаемой задачи разбивается на ряд подмножеств. Для
- 5. СТРАТЕГИИ ВЕТВЛЕНИЯ Приняты две основные стратегии построения дерева ветвлений: Фронтальный спуск по дереву ветвлений. Движение по
- 6. ЧАСТЬ 2 МЕТОДЫ ТИПА ВЕТВЕЙ И ГРАНИЦ, ОСУЩЕСТВЛЯЮЩИЕ ПОИСК МИНИМАЛЬНОГО РАЗРЕЗА НА БИСВЯЗНОМ ГРАФЕ ФРОНТАЛЬНЫМ СПУСКОМ
- 7. ИДЕЯ ФРОНТАЛЬНОГО СПУСКА ПО ДЕРЕВУ ВЕТВЛЕНИЙ Три основных шага построения дерева ветвлений фронтальным спуском: 1. На
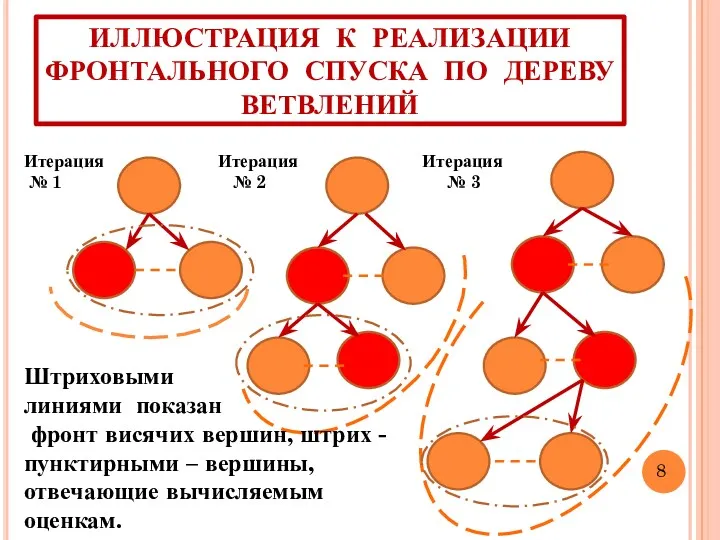
- 8. ИЛЛЮСТРАЦИЯ К РЕАЛИЗАЦИИ ФРОНТАЛЬНОГО СПУСКА ПО ДЕРЕВУ ВЕТВЛЕНИЙ Штриховыми линиями показан фронт висячих вершин, штрих -
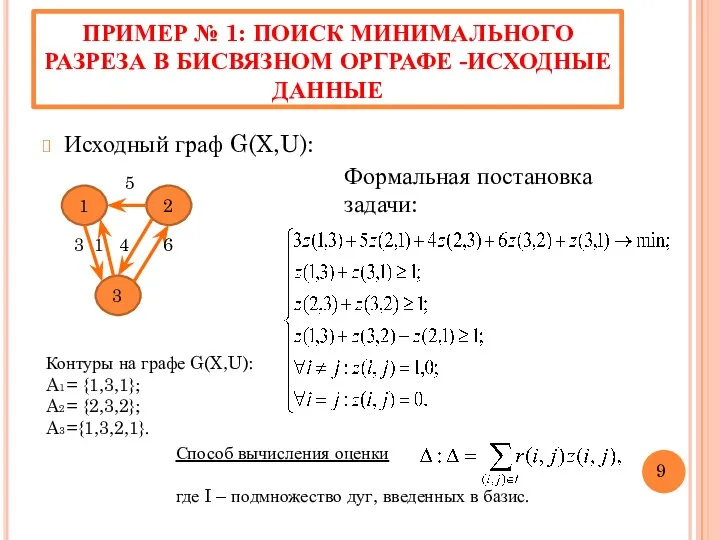
- 9. ПРИМЕР № 1: ПОИСК МИНИМАЛЬНОГО РАЗРЕЗА В БИСВЯЗНОМ ОРГРАФЕ -ИСХОДНЫЕ ДАННЫЕ Исходный граф G(X,U): 1 2
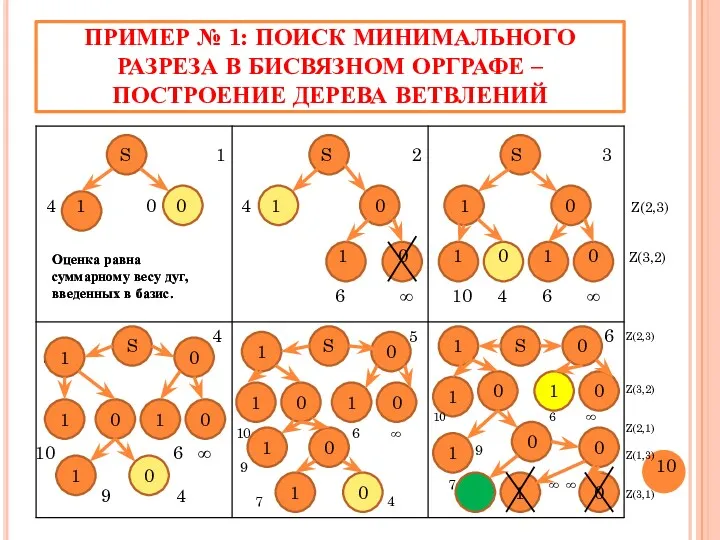
- 10. ПРИМЕР № 1: ПОИСК МИНИМАЛЬНОГО РАЗРЕЗА В БИСВЯЗНОМ ОРГРАФЕ – ПОСТРОЕНИЕ ДЕРЕВА ВЕТВЛЕНИЙ 4 1 0
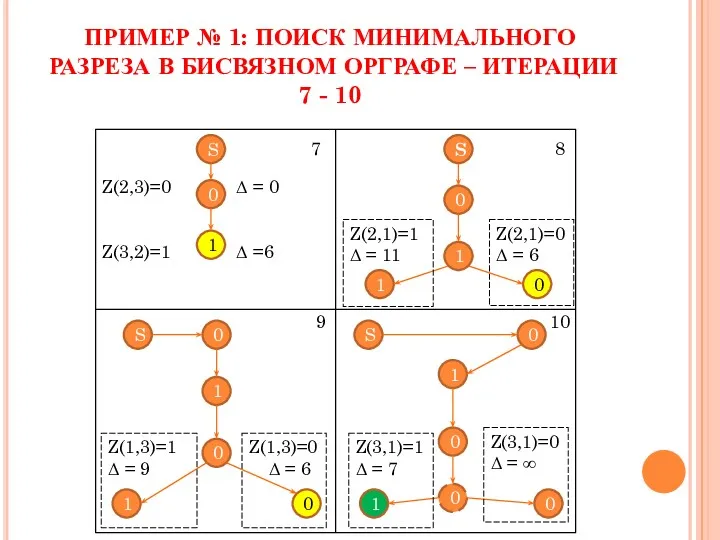
- 11. Z(1,3)=0 Δ = 6 Z(2,1)=0 Δ = 6 ПРИМЕР № 1: ПОИСК МИНИМАЛЬНОГО РАЗРЕЗА В БИСВЯЗНОМ
- 12. ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ В ПРИМЕРЕ 1 Число вычисленных оценок: 12. Число итераций: 6. Число операций сравнения:
- 13. Достоинства и недостатки фронтального спуска по дереву ветвлений Достоинства: шанс на неполный перебор, первый же полный
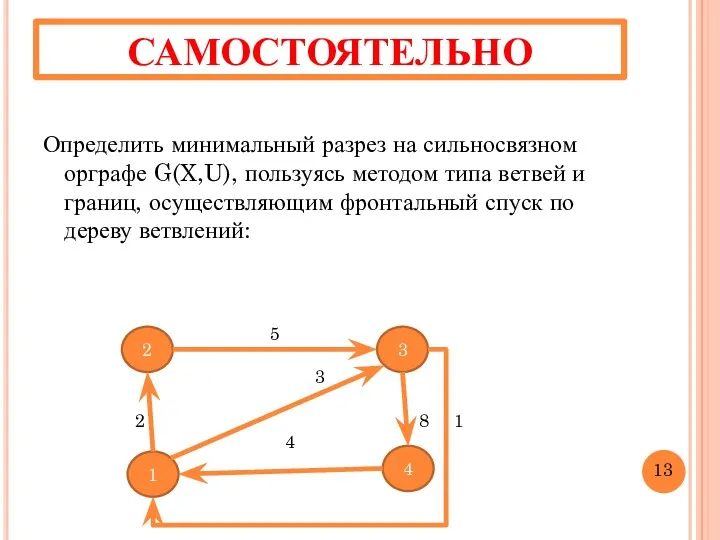
- 14. Определить минимальный разрез на сильносвязном орграфе G(X,U), пользуясь методом типа ветвей и границ, осуществляющим фронтальный спуск
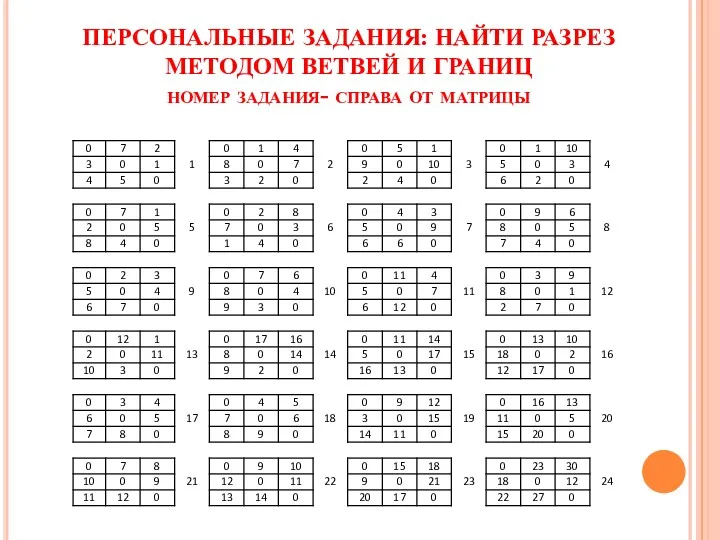
- 15. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ: НАЙТИ РАЗРЕЗ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ номер задания- справа от матрицы
- 16. ИСПОЛЬЗОВАНИЕ ЦИРКУЛЯЦИЙ ДЛЯ УТОЧНЕНИЯ ОЦЕНКИ Теорема В.Н. Буркова: Величина максимальной циркуляции не превышает величины минимального разреза.
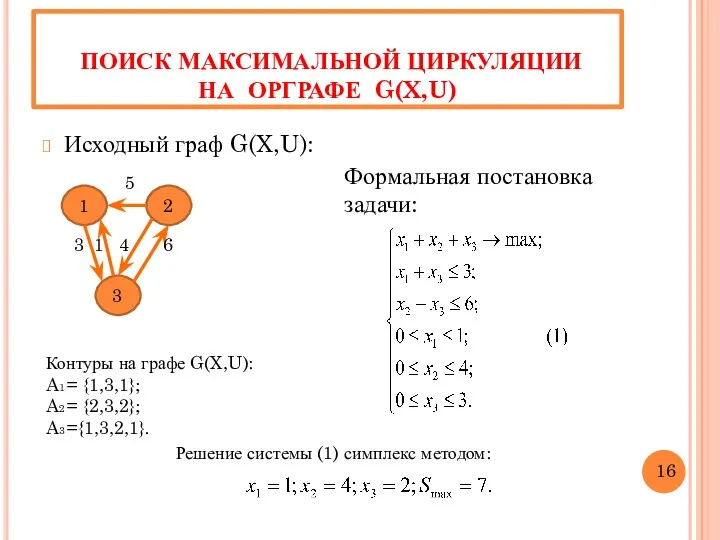
- 17. ВЫЧИСЛЕНИЕ МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ НА ГРАФЕ G(X,U) Формальная постановка задачи определения S(G’): Контуры на графе: a1 =
- 18. ПОИСК МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ НА ОРГРАФЕ G(X,U) Исходный граф G(X,U): 1 2 3 3 1 4 6
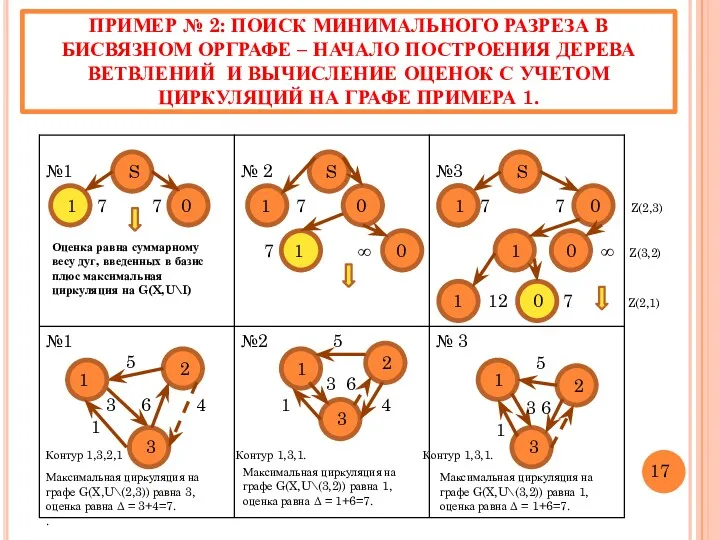
- 19. ПРИМЕР № 2: ПОИСК МИНИМАЛЬНОГО РАЗРЕЗА В БИСВЯЗНОМ ОРГРАФЕ – НАЧАЛО ПОСТРОЕНИЯ ДЕРЕВА ВЕТВЛЕНИЙ И ВЫЧИСЛЕНИЕ
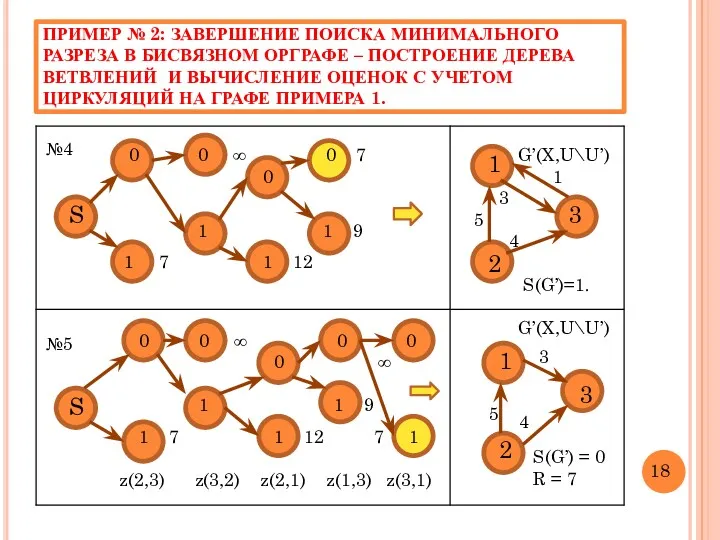
- 20. ПРИМЕР № 2: ЗАВЕРШЕНИЕ ПОИСКА МИНИМАЛЬНОГО РАЗРЕЗА В БИСВЯЗНОМ ОРГРАФЕ – ПОСТРОЕНИЕ ДЕРЕВА ВЕТВЛЕНИЙ И ВЫЧИСЛЕНИЕ
- 21. ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ В ПРИМЕРЕ 2 (вычисление уточненных оценок) Число вычисленных оценок: 10. Число итераций: 5.
- 22. ДОСТОИНСТВА И НЕДОСТАТКИ ФРОНТАЛЬНОГО СПУСКА Достоинства: - гарантия глобально оптимального решения; - первый же выбранный полный
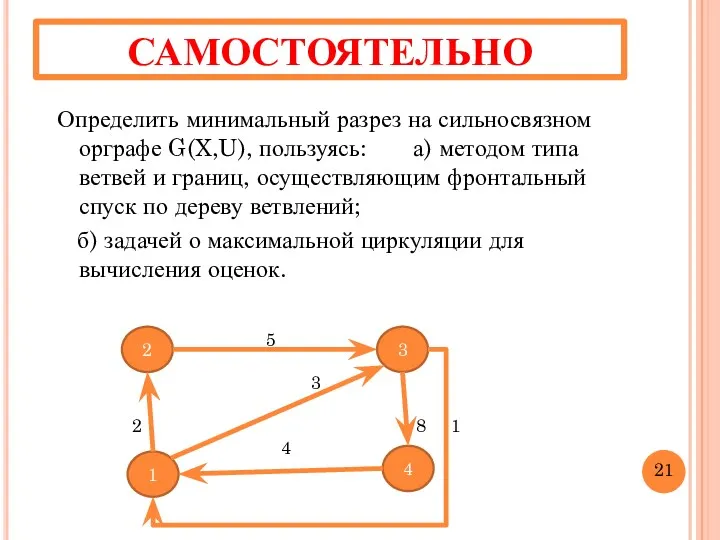
- 23. САМОСТОЯТЕЛЬНО Определить минимальный разрез на сильносвязном орграфе G(X,U), пользуясь: а) методом типа ветвей и границ, осуществляющим
- 24. САМОСТОЯТЕЛЬНО 2 Найти минимальный разрез на орграфе, приведенном в списке персональных заданий, пользуясь: Методом типа ветвей
- 25. ЧАСТЬ 3 МЕТОДЫ ТИПА ВЕТВЕЙ И ГРАНИЦ, ОСУЩЕСТВЛЯЮЩИЕ ПОИСК МИНИМАЛЬНОГО РАЗРЕЗА НА БИСВЯЗНОМ ГРАФЕ ДВИЖЕНИЕМ ПО
- 26. ОСНОВНЫЕ ЭТАПЫ СТРАТЕГИИ ПОИСКА МИНИМАЛЬНОГО РАЗРЕЗА НА ДЕРЕВЕ ВЕТВЛЕНИЙ С ВОЗВРАТОМ В памяти компьютера постоянно присутствуют
- 27. АЛГОРИТМ ПОИСКА МИНИМАЛЬНОГО РАЗРЕЗА НА БИСВЯЗНОМ ГРАФЕ МЕТОДОМ ТИПА ВЕТВЕЙ И ГРАНИЦ, ОСУЩЕСТВЛЯЮЩИЙ ДВИЖЕНИЕ ПО ДЕРЕВУ
- 28. ПРОДОЛЖЕНИЕ АЛГОРИТМА ПОИСКА МИНИМАЛЬНОГО РАЗРЕЗА НА БИСВЯЗНОМ ГРАФЕ МЕТОДОМ ТИПА ВЕТВЕЙ И ГРАНИЦ, ОСУЩЕСТВЛЯЮЩИМ ДВИЖЕНИЕ ПО
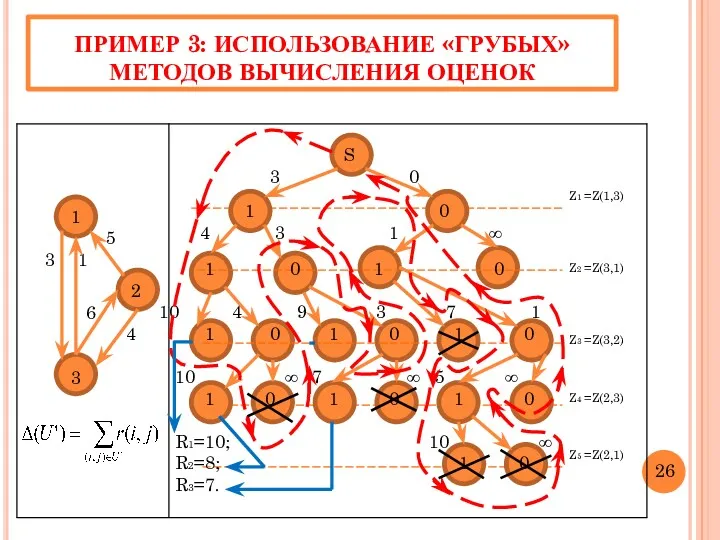
- 29. ПРИМЕР 3: ИСПОЛЬЗОВАНИЕ «ГРУБЫХ» МЕТОДОВ ВЫЧИСЛЕНИЯ ОЦЕНОК 1 5 1 2 6 4 3 Z1 =Z(1,3)
- 30. ИТОГИ ПОИСКА РЕШЕНИЯ В ПРИМЕРЕ 3 Число вычисленных оценок – 20 Число итераций – 20 Число
- 31. САМОСТОЯТЕЛЬНО Определить минимальный разрез на сильносвязном орграфе G(X,U), пользуясь методом типа ветвей и границ, осуществляющим поиск
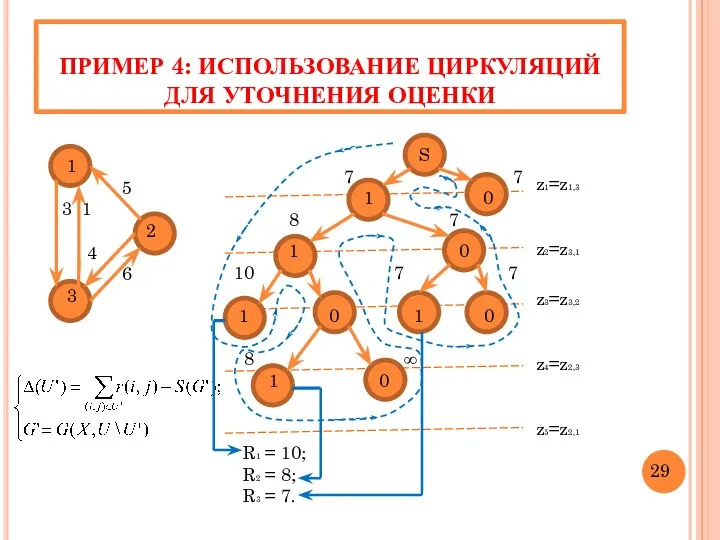
- 32. ПРИМЕР 4: ИСПОЛЬЗОВАНИЕ ЦИРКУЛЯЦИЙ ДЛЯ УТОЧНЕНИЯ ОЦЕНКИ 1 5 3 1 2 4 6 3 S
- 33. ИТОГИ ПОИСКА РЕШЕНИЯ В ПРИМЕРЕ 4 Число вычисленных оценок – 10 Число итераций – 10 Число
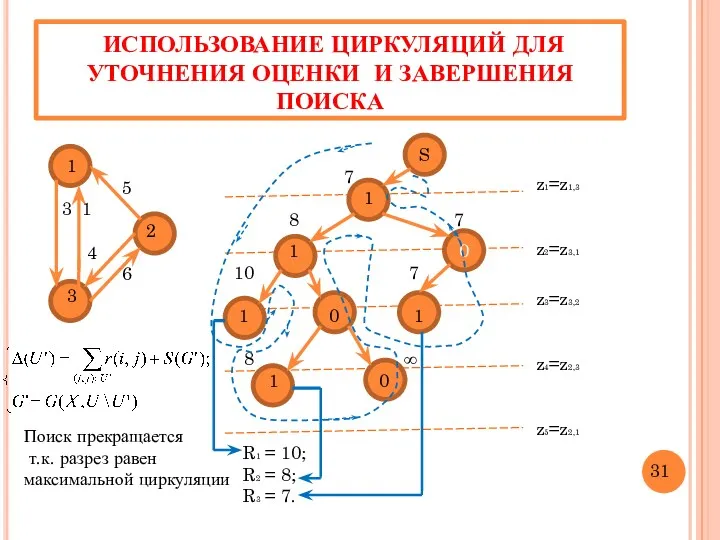
- 34. ИСПОЛЬЗОВАНИЕ ЦИРКУЛЯЦИЙ ДЛЯ УТОЧНЕНИЯ ОЦЕНКИ И ЗАВЕРШЕНИЯ ПОИСКА 1 5 3 1 2 4 6 3
- 35. ИТОГИ ПОИСКА РЕШЕНИЯ В ПРИМЕРЕ 4 Число вычисленных оценок – 8 Число итераций – 8 Число
- 36. ДОСТОИНСТВА И НЕДОСТАТКИ СТРАТЕГИИ, РЕАЛИЗУЮЩЕЙ ПОИСК С ВОЗВРАТОМ Достоинства: гарантия глобально оптимального решения; возможность прервать поиск
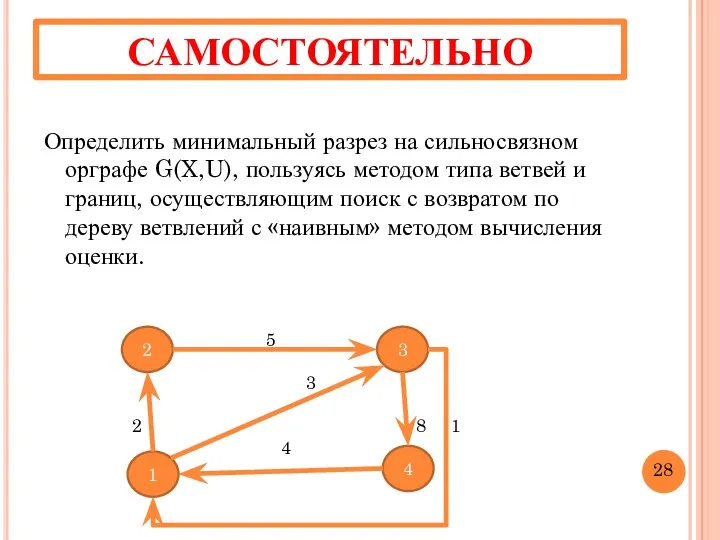
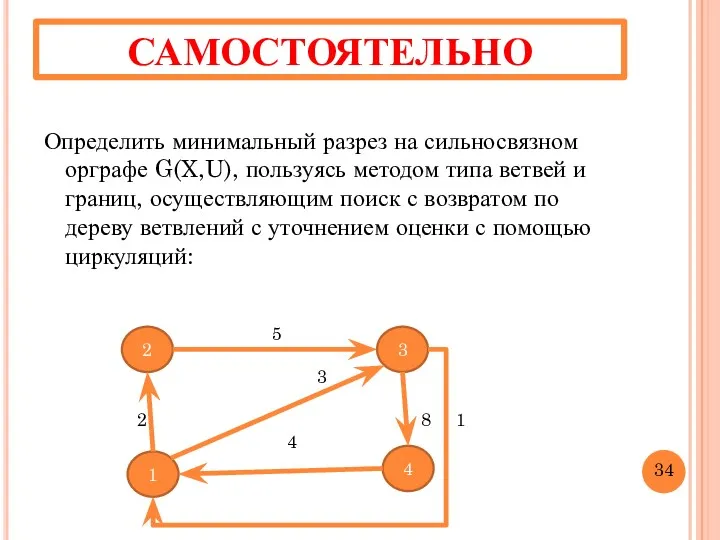
- 37. САМОСТОЯТЕЛЬНО Определить минимальный разрез на сильносвязном орграфе G(X,U), пользуясь методом типа ветвей и границ, осуществляющим поиск
- 39. Скачать презентацию





















 Компьютерная мышь
Компьютерная мышь Введение в язык программирования Python
Введение в язык программирования Python Операционная система. Программное обеспечение компьютера
Операционная система. Программное обеспечение компьютера Информационные технологии. Основы программирования на Python 3
Информационные технологии. Основы программирования на Python 3 Елементи для введення даних: текстове поле, прапорець, випадаючий список
Елементи для введення даних: текстове поле, прапорець, випадаючий список Операционная система Windows
Операционная система Windows Знакомство с языком программирования QBasic
Знакомство с языком программирования QBasic Модели систем
Модели систем Правила юзабилити для сайтов
Правила юзабилити для сайтов Представление и обработка информации в интеллектуальных системах
Представление и обработка информации в интеллектуальных системах Introduction to computer systems. Architecture of computer systems
Introduction to computer systems. Architecture of computer systems ООП на Delphi - 1. Знакомство с системой программирования Borland Delphi
ООП на Delphi - 1. Знакомство с системой программирования Borland Delphi Основы журналистики
Основы журналистики Морское приключение
Морское приключение Кодирование графической информации
Кодирование графической информации Текст и виды информации Microsoft Office PowerPoint
Текст и виды информации Microsoft Office PowerPoint Подходы к понятию информация
Подходы к понятию информация Логика — это наука о формах и способах мышления
Логика — это наука о формах и способах мышления Устройство компьютера, информатика 8 класс
Устройство компьютера, информатика 8 класс Использование системных ресурсов. Организация ввода-вывода численных данных
Использование системных ресурсов. Организация ввода-вывода численных данных Коучинг по Facebook и Mytarget
Коучинг по Facebook и Mytarget Типы данных АСДП
Типы данных АСДП Понятие информации, ее виды и формы
Понятие информации, ее виды и формы Тема урока: Практическая работа №2 Измерение информации 10-классе(презентация)
Тема урока: Практическая работа №2 Измерение информации 10-классе(презентация) Ақпараттық жүйелер ұғымы. Ақпараттық жүйелердің құрылымы
Ақпараттық жүйелер ұғымы. Ақпараттық жүйелердің құрылымы Таймлайн нейронной сети
Таймлайн нейронной сети Структурное программирование. Основные сведения об алгоритмах
Структурное программирование. Основные сведения об алгоритмах Разработка обучающего модуля для работы с генетическими алгоритмами
Разработка обучающего модуля для работы с генетическими алгоритмами