Содержание
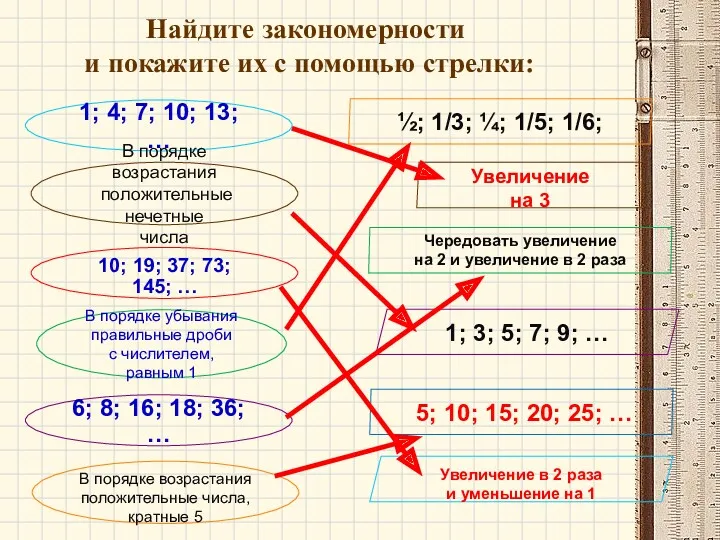
- 2. Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; … В порядке
- 3. Что такое числовая последовательность? Если каждому натуральному числу п поставлено в соответствие некоторое действительное число хп
- 4. Способы задания последовательности Рекуррентный (от лат. слова recurrens – «возвращающийся») Аналитический Словесный Рекуррентный
- 5. Словесный способ. Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности
- 6. Аналитический способ. с помощью формулы. Пример 1. Последовательность чётных чисел: y = 2n; 2, 4, 6,
- 7. Рекуррентный способ. Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы. Пример 1.
- 8. Предел числовой последовательности Рассмотрим две числовые последовательности: : 2, 4, 6, 8, 10, …, 2п ,…;
- 9. Замечаем, что члены последовательности уп как бы «сгущаются» около точки 0, а у последовательности хп таковой
- 10. Определение 1. Пусть a - точка прямой, а r положительное число. Интервал (a-r, a+r) называют окрестностью
- 11. Теперь можно перейти к определению точки «сгущения», которую математики назвали «пределом последовательности». Например (-0.1, 0.5) –
- 12. Число b называется пределом последовательности {уп } если в любой заранее выбранной окрестности точки b содержатся
- 13. Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
- 14. Рассмотрим последовательность: – гармонический ряд Если │q│ Если │q│> 1, то последовательность уn = q n
- 15. Свойства пределов предел частного равен частному пределов: предел произведения равен произведению пределов: предел суммы равен сумме
- 16. Примеры:
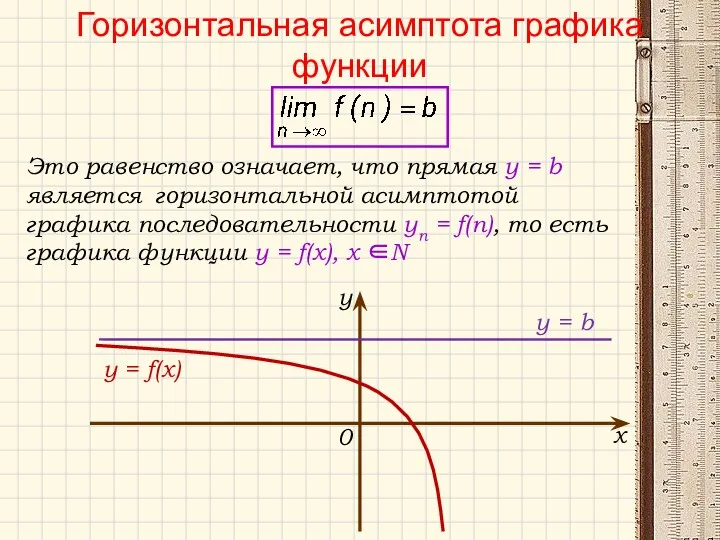
- 17. Это равенство означает, что прямая у = b является горизонтальной асимптотой графика последовательности yn = f(n),
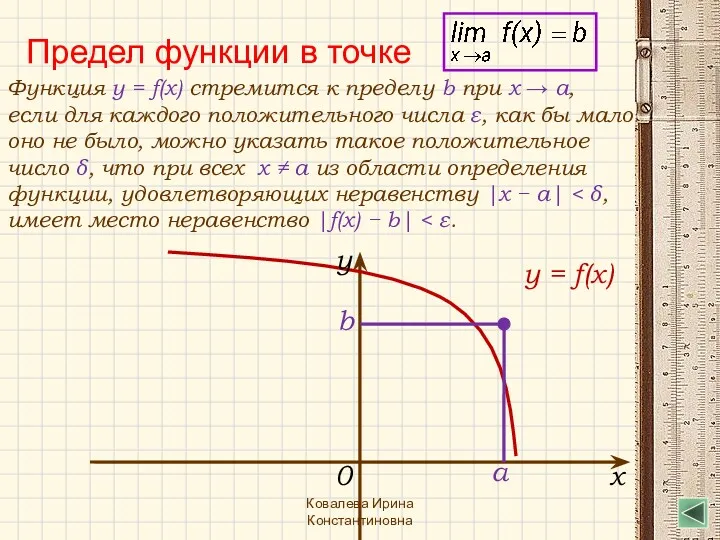
- 18. Предел функции в точке Функция y = f(x) стремится к пределу b при x → a,
- 19. Непрерывность функции в точке Функцию y = f(x) называют непрерывной в точке x = a, если
- 20. Понятие непрерывности функции На рисунке изображен график функции, состоящий из двух «кусков». Каждый из них может
- 25. Скачать презентацию















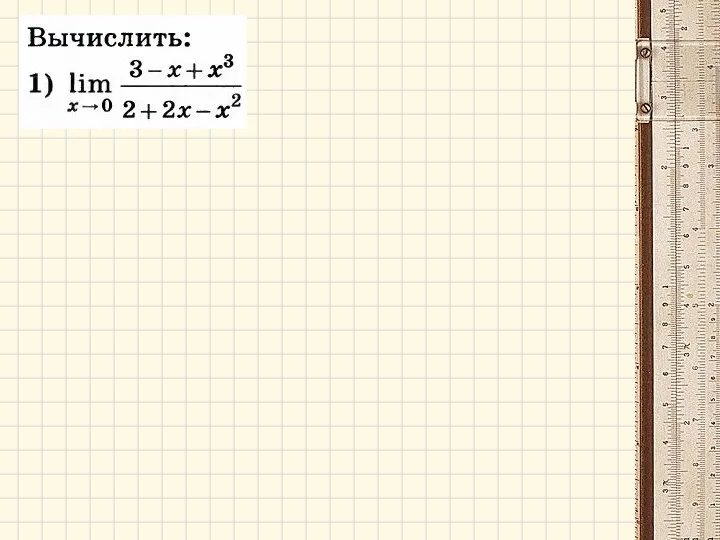
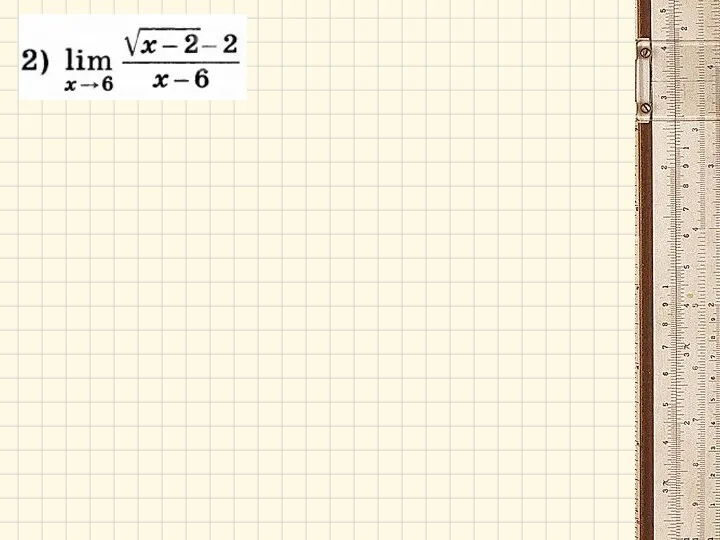
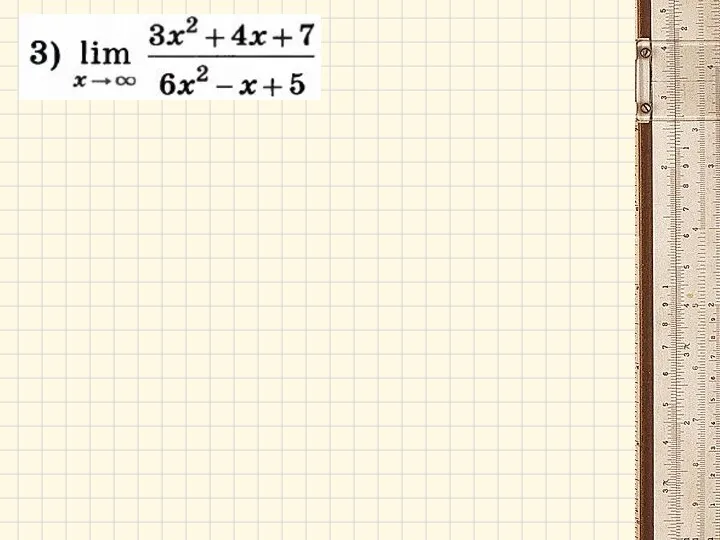
 Связь между бесконечно малыми и бесконечно большими величинами
Связь между бесконечно малыми и бесконечно большими величинами Сфера и шар
Сфера и шар Презентация к уроку математики в 4 классе Задачи на движение
Презентация к уроку математики в 4 классе Задачи на движение Геометрический смысл производной
Геометрический смысл производной Интерактивный тренажёр Сложение и вычитание чисел в пределах 100
Интерактивный тренажёр Сложение и вычитание чисел в пределах 100 Модуль числа (часть 1)
Модуль числа (часть 1) Система обобщающего повторения на уроках геометрии при подготовке к ГИА
Система обобщающего повторения на уроках геометрии при подготовке к ГИА График функции
График функции Аксонометрия
Аксонометрия Математика. Раздел 7. Функции и графики
Математика. Раздел 7. Функции и графики Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Задачи на нахождение процентов
Задачи на нахождение процентов Гномы 2(математические тренинги)
Гномы 2(математические тренинги) Алгоритм сложения трёхзначных чисел.
Алгоритм сложения трёхзначных чисел. Решение квадратных неравенств. 8 класс
Решение квадратных неравенств. 8 класс Алгоритми і виконавці
Алгоритми і виконавці Решение квадратных уравнений по формуле. 8 класс
Решение квадратных уравнений по формуле. 8 класс Основы математической обработки информации
Основы математической обработки информации Задача по финансовой математике
Задача по финансовой математике Принцип Дирихле
Принцип Дирихле Сложения и вычитания десятичных дробей
Сложения и вычитания десятичных дробей Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Формирование понятия об арифметических действиях и их свойствах в начальной школе
Формирование понятия об арифметических действиях и их свойствах в начальной школе Задачи на построение. 7 класс
Задачи на построение. 7 класс вероятность с теорией
вероятность с теорией Банк мультимедийных презентаций по ФЭМП
Банк мультимедийных презентаций по ФЭМП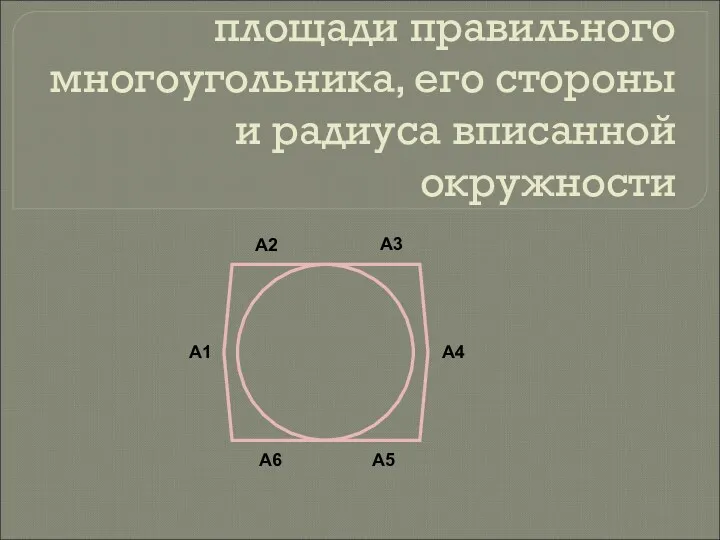 Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Делители и кратные. 5 класс
Делители и кратные. 5 класс