Содержание
- 2. Содержание Определение промежутков возрастания и убывания функции (исследование функции на монотонность) Нахождение точек экстремума функции Построение
- 3. Исследование функции на монотонность (т.е. определение промежутков возрастания и убывания функции).
- 4. Исследовать функцию на монотонность – это значит выяснить, на каких промежутках из области определения функция возрастает,
- 5. Вспомним
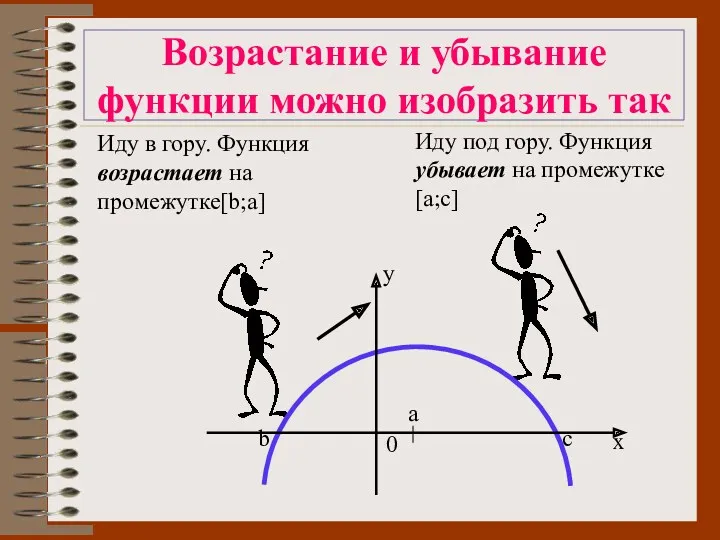
- 6. Возрастание и убывание функции можно изобразить так Иду в гору. Функция возрастает на промежутке[b;a] Иду под
- 7. Для определения промежутков возрастания и убывания функции можно использовать и производную .
- 8. Теорема: Если f(x) – непрерывна на промежутке и имеет f´(x), то а) если f´(x) > 0,
- 9. Алгоритм исследования функции на монотонность Найти производную функции f ΄(х) Найти стационарные (f ΄(х) = 0)
- 10. Определения Внутренние точки области определения функции, в которых производная функции равна нулю, называются стационарными. Внутренние точки
- 11. Например: найти промежутки монотонности функции f(x) = x³ - 6x² + 9x – 1 1) f´(x)
- 12. Найти промежутки монотонности функции у = 2х³ +3х² -100 у = х³ + 2х² + 6
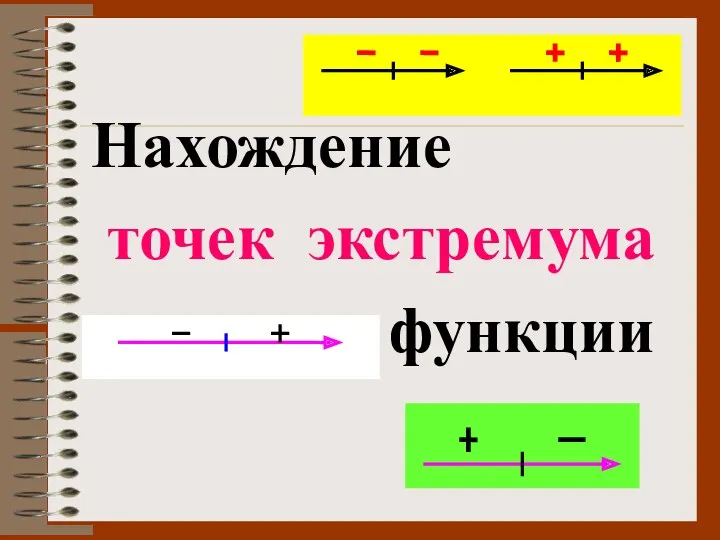
- 13. Нахождение точек экстремума функции
- 14. Определения Точка хо называется точкой минимума функции у = f(х), если у этой точки существует окрестность,
- 15. Определения Значение функции в точке максимума обозначают уmax (но на определенном участке вокруг точки максимума, а
- 16. Теорема Пусть функция у = f(х) непрерывна на промежутке Х и имеет внутри промежутка стационарную или
- 17. б) если у этой точки существует такая окрестность, в которой при х 0, а при х>х0
- 18. в) если у этой точки существует такая окрестность, что в ней и слева и справа от
- 19. Алгоритм нахождения точек экстремума функции Найти производную функции f ΄(х) Найти стационарные и критические точки функции
- 20. Например: найти точки экстремума функции Решение. 1) у΄=12 х³ - 48х² + 48х = = 12х(х²-4х+4)
- 21. Найдите точки экстремума функции и определите их характер у = 7 + 12х - х² у
- 22. Построение графиков функций
- 23. В тех случаях, когда речь идет о построении графика незнакомой функции или когда заранее трудно представить
- 24. План построения графика функции с помощью производной Найти область определения функции и определить точки разрыва если
- 25. Как найти промежутки выпуклости, вогнутости и точку перегиба графика функции Промежутки выпуклости и вогнутости кривой можно
- 26. Для нахождения интервалов выпуклости графика функции используют следующий алгоритм: Находят f΄(х), а затем f ΄΄(х) Находят
- 27. Точкой перегиба кривой называется такая точка, которая отделяет выпуклую часть кривой от вогнутой её части. Точкой
- 28. Найти интервалы выпуклости и точку перегиба функции Решение. Найдем у΄(х) и у΄΄(х): у΄(х) = 4х³-12х =>
- 29. Например: исследовать функцию у = 2х³+3х² -1 и построить её график Решение. D(у)= (-∞; +∞), четность
- 30. Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞) - функция возрастает при
- 31. Найдем ещё некоторые точки (контрольные, дополнительные): т.к. х=-1 – точка максимума, то уmax=0 => (-1; 0)
- 32. Составим таблицу: Найдем f ΄΄(х). f΄΄(х) =(6х(х+1))΄=12х+6 = 6(2х+1) f΄΄(х)=0 => 6(2х+1)=0 => х = -0,5
- 33. Построим график функции: х у 0 -1 -2 4 1 -5
- 34. Исследовать функцию и построить её график 1) у = 3х² - х³ 2) у = -
- 35. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
- 36. Теорема Дифференцируемая на (а;b) и непрерывная на [a;b] функция у=f(x) достигает своего наибольшего (наименьшего) значения на
- 37. Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у=f(х) на отрезке [а;в] 1) Найти производную f
- 38. Например: найти наименьшее и наибольшее значения функции у= х³ - 3х² - 45х + 1 на
- 39. Решение. б) на [-2;2] 1) у΄= 3х² - 6х – 45 2) у΄= 0 => 3х²
- 40. Самостоятельно найдите наименьшее и наибольшее значения функции у= х³ - 3х² - 45х + 1 на
- 41. Найдите наименьшее и наибольшее значения функции на заданном промежутке. 1) у = х²-8х+19 на [-1;5] 2)
- 42. Работа с графиками функций
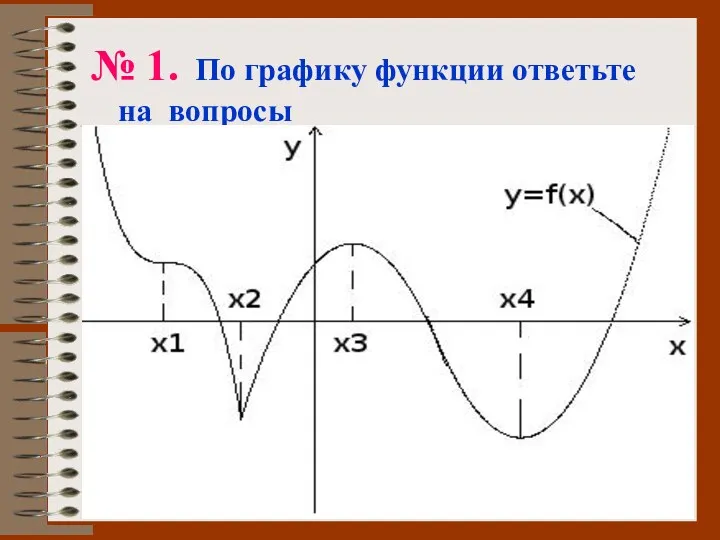
- 43. № 1. По графику функции ответьте на вопросы
- 44. 1) Отметьте стационарные точки. 2) Что можно сказать о производной в точке х1? 3) Назовите точки
- 45. Проверим ответы 1. (х1,х3,х4). 2. не существует. 3. (х2,х3,х4). 4. f′(х) ≤ 0. 5. [х2; х3]U
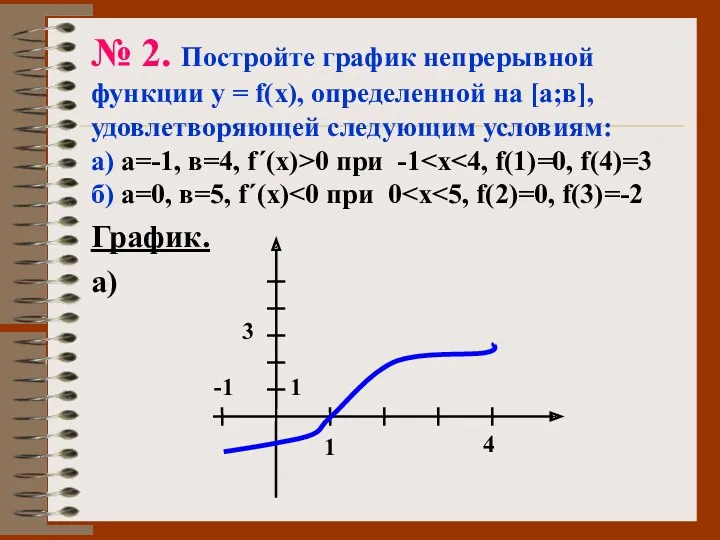
- 46. № 2. Постройте график непрерывной функции у = f(х), определенной на [а;в], удовлетворяющей следующим условиям: а)
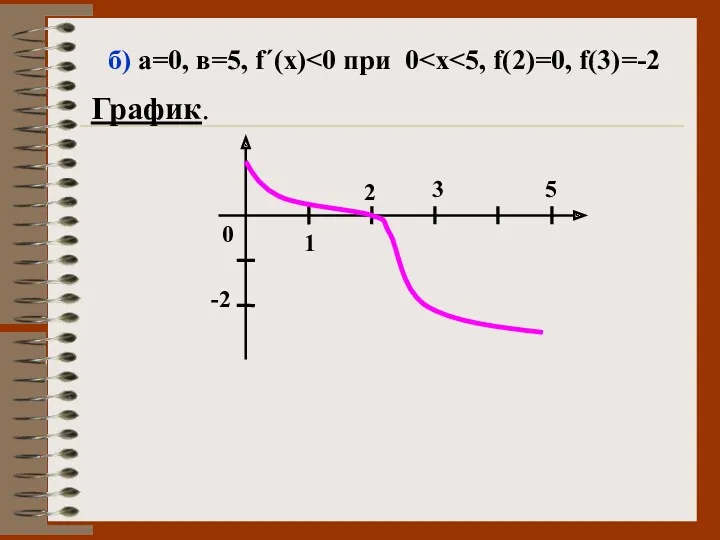
- 47. б) а=0, в=5, f΄(х) График. 0 -2 3 5 2 1
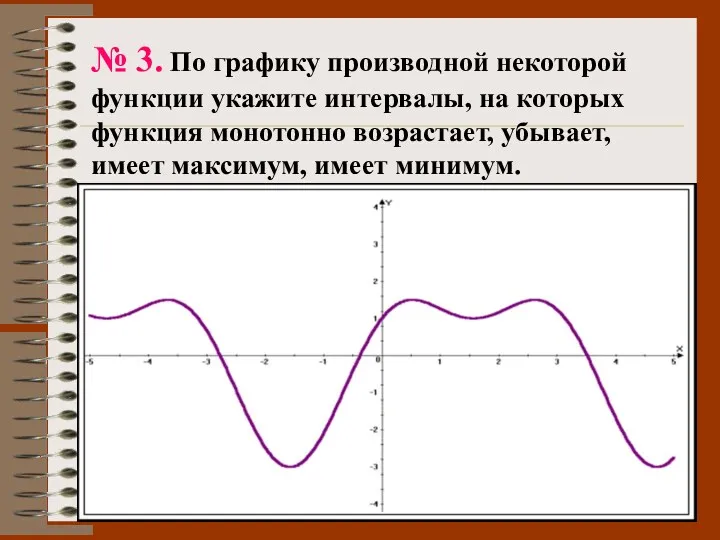
- 48. № 3. По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет
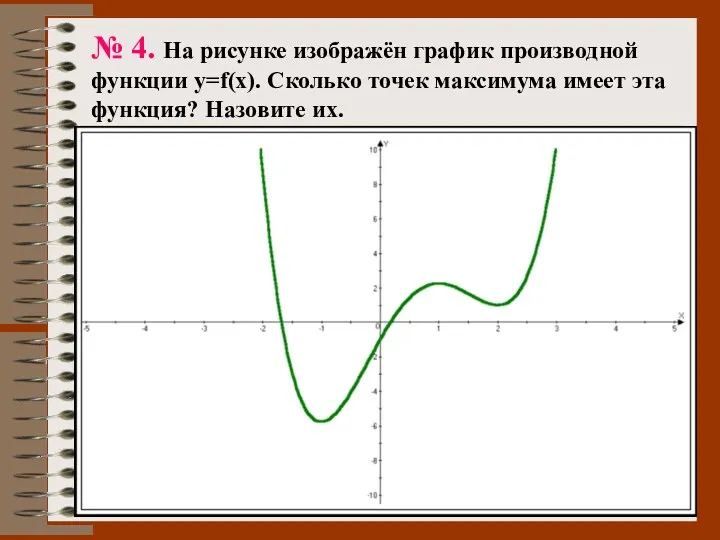
- 49. № 4. На рисунке изображён график производной функции y=f(x). Сколько точек максимума имеет эта функция? Назовите
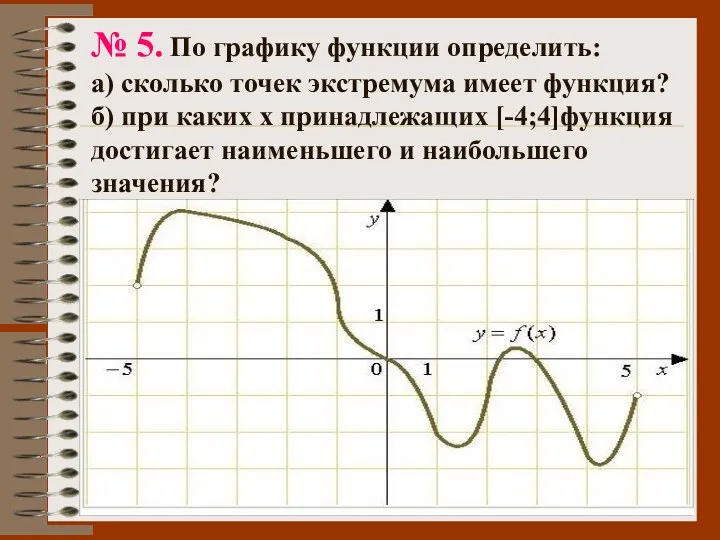
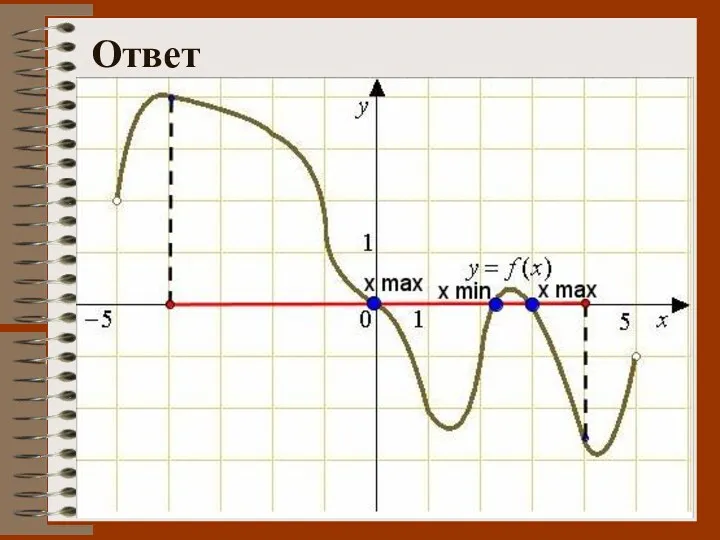
- 50. № 5. По графику функции определить: а) сколько точек экстремума имеет функция? б) при каких х
- 51. Ответ
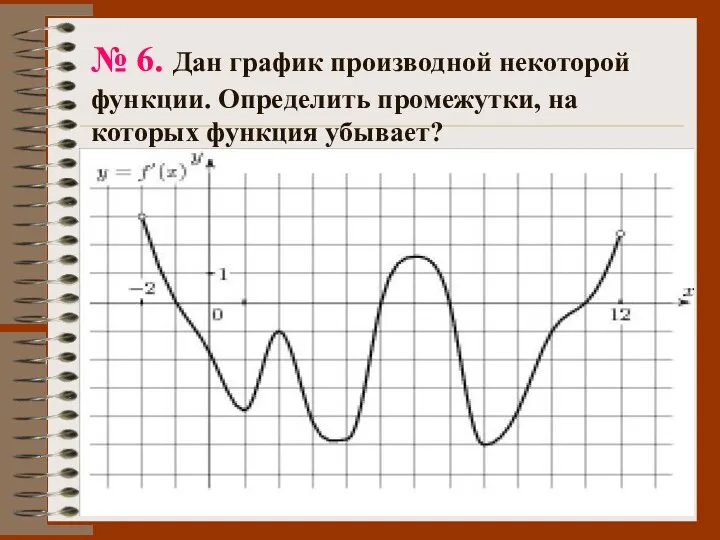
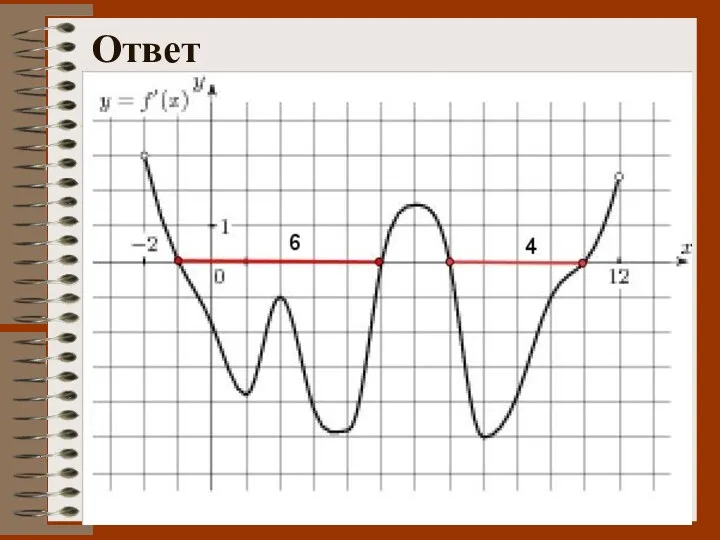
- 52. № 6. Дан график производной некоторой функции. Определить промежутки, на которых функция убывает?
- 53. Ответ
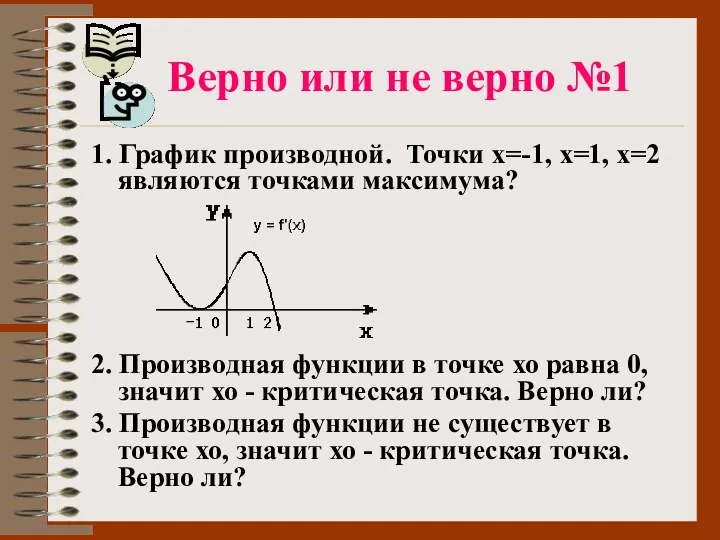
- 54. Верно или не верно №1 1. График производной. Точки х=-1, х=1, х=2 являются точками максимума? 2.
- 55. 4. Критическая точка является точкой экстремума. Верно ли? 5. Точка экстремума является критической точкой. Верно ли?
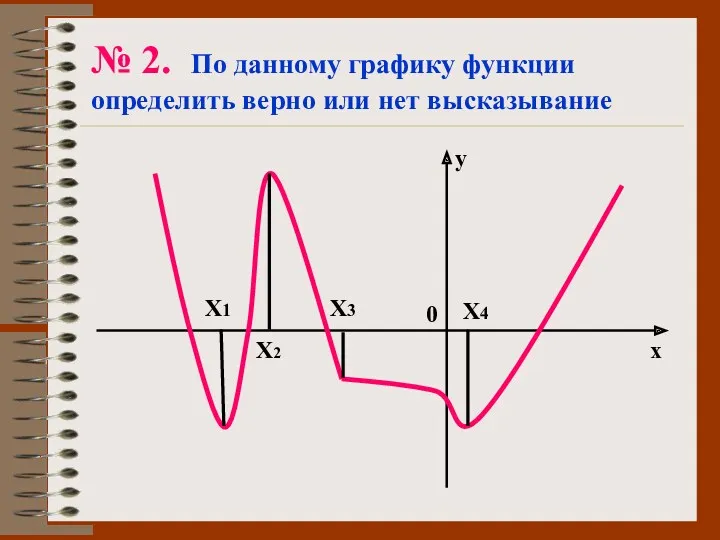
- 56. № 2. По данному графику функции определить верно или нет высказывание 0 х у Х1 Х2
- 57. Точка х1 – точка минимума. Точка х1 – точка перегиба. В точках х2 и х4 касательная
- 59. Скачать презентацию























![Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/607533/slide-29.jpg)




![Теорема Дифференцируемая на (а;b) и непрерывная на [a;b] функция у=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/607533/slide-35.jpg)


![Решение. б) на [-2;2] 1) у΄= 3х² - 6х –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/607533/slide-38.jpg)






 Интегрированный урок История и математика (6 класс)
Интегрированный урок История и математика (6 класс)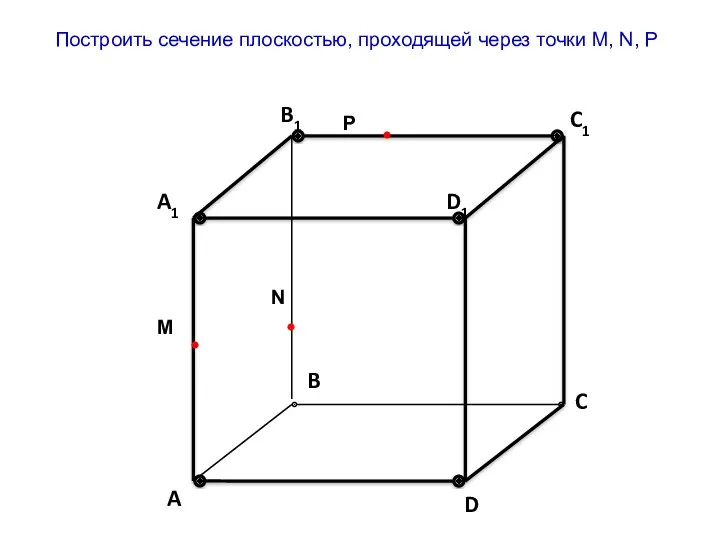 Построение сечения плоскостью
Построение сечения плоскостью Методы кибернетики
Методы кибернетики Параллелепипед. Геометрия. 10 класс
Параллелепипед. Геометрия. 10 класс Приёмы устных вычислений вида 100 разд. на 50
Приёмы устных вычислений вида 100 разд. на 50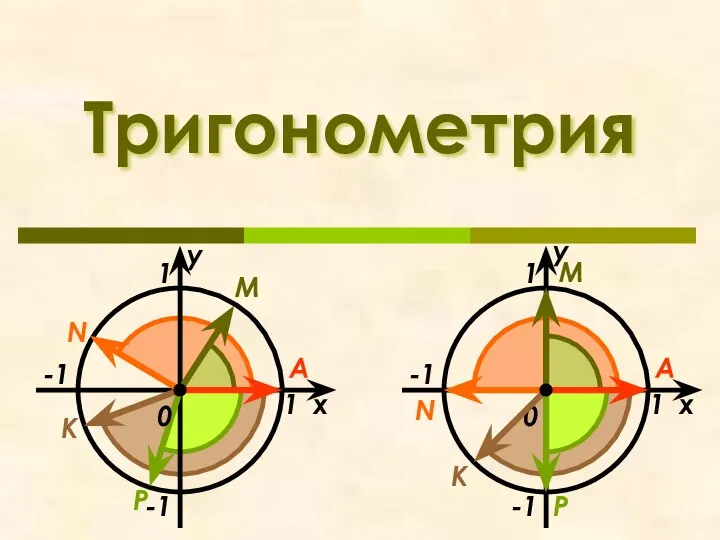 Тригонометрия
Тригонометрия Числовой набор
Числовой набор Дифференциал функции
Дифференциал функции Дискретные структуы. Теория графов. Основные понятия
Дискретные структуы. Теория графов. Основные понятия Сучасні методи наближення функцій багатьох змінних (інтерлінація)
Сучасні методи наближення функцій багатьох змінних (інтерлінація) Обучение детей измерению с помощью общепринятыхединиц измерения: см, дм, м
Обучение детей измерению с помощью общепринятыхединиц измерения: см, дм, м Координатна пряма. Математика. 6 клас
Координатна пряма. Математика. 6 клас Десятичная запись дробей
Десятичная запись дробей Параллельные прямые и секущие. Задания для устного счета. Упражнение 8. 7 класс
Параллельные прямые и секущие. Задания для устного счета. Упражнение 8. 7 класс Умножение десятичных дробей
Умножение десятичных дробей Формулы сложения
Формулы сложения ОГЭ 2016. Модуль Алгебра №2
ОГЭ 2016. Модуль Алгебра №2 Descriptive statistics. Frequency distributions and their graphs. (Section 2.1)
Descriptive statistics. Frequency distributions and their graphs. (Section 2.1) Анализ одномерных распределений
Анализ одномерных распределений Метод анализа иерархий (МАИ)
Метод анализа иерархий (МАИ) Экспоненциальные методы для анализа временных рядов
Экспоненциальные методы для анализа временных рядов Математика. 1 класс. Урок 95. Табличное сложение и вычитание - Презентация
Математика. 1 класс. Урок 95. Табличное сложение и вычитание - Презентация Алгебра и начала анализа 10 – 11 класс. Муравин Георгий Константинович, Муравина Ольга Викторовна
Алгебра и начала анализа 10 – 11 класс. Муравин Георгий Константинович, Муравина Ольга Викторовна Развёртка прямоугольного параллелепипеда. Урок 143
Развёртка прямоугольного параллелепипеда. Урок 143 Длина окружности и площадь круга
Длина окружности и площадь круга Свойства прямой и обратной функций
Свойства прямой и обратной функций Системы с нечеткой логикой. Лекция 21-22
Системы с нечеткой логикой. Лекция 21-22 Математическое моделирование. Движение по градиенту
Математическое моделирование. Движение по градиенту