Содержание
- 2. 4.2. Интерполяция многочленами
- 3. Если приближение строится на заданном дискретном множестве точек {xi}, то аппроксимация называется точечной. При построении приближения
- 4. Теорема. Какие бы ни были заданы значения функции в n+1 узлах, всегда существует и притом единственный
- 6. 4.3. Погрешность интерполирования Погрешность аппроксимации функции f (x) полиномом ϕ(x ) можно оценивать по величине среднеквадратичного
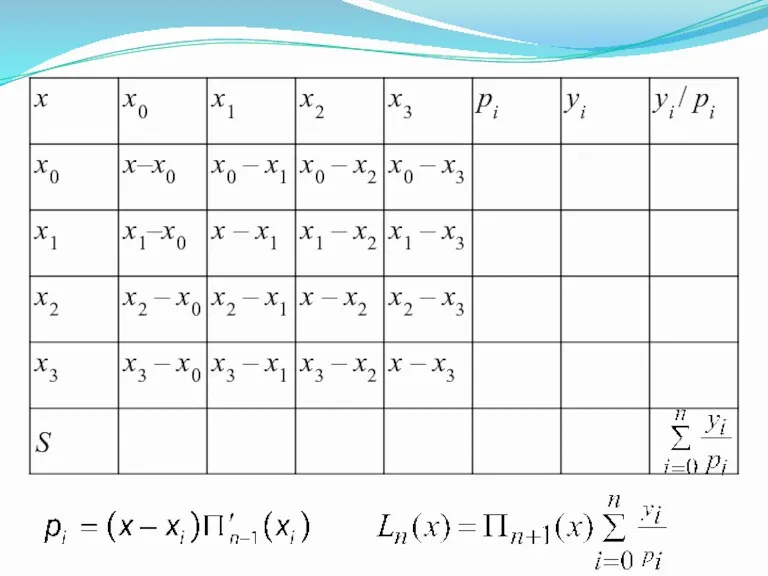
- 7. 4.4. Интерполяционный многочлен Лагранжа
- 10. Пример. Построить интерполяционный многочлен Лагранжа для функции заданной таблицей. =
- 11. Пример. Построить интерполяционный многочлен Лагранжа для функции заданной таблицей. =
- 14. Погрешность формулы Лагранжа
- 15. Многочлен Лагранжа для равноудаленных узлов
- 18. 4.5. Интерполяционные многочлены Ньютона Конечной разностью первого порядка называется разность между двумя соседними значениями функции f:
- 19. Таблица конечных разностей
- 20. Первый интерполяционный многочлен Ньютона для равноотстоящих узлов Используется тогда, когда точка, в которой требуется вычислить приближенное
- 21. Первая интерполяционная формула Ньютона. Используется для интерполирования вперед и экстраполирования назад.
- 22. Второй интерполяционный многочлен Ньютона для равноотстоящих узлов Используется тогда, когда точка, в которой требуется вычислить приближенное
- 23. Вторая интерполяционная формула Ньютона. Используется для интерполирования назад и экстраполирования вперед.
- 28. Интерполяционные многочлены Ньютона для неравноотстоящих узлов Разделенными разностями первого порядка называются отношения:
- 29. Разделенными разностями порядка k называются отношения:
- 30. Первый интерполяционный многочлен Ньютона с разделенными разностями
- 31. Второй интерполяционный многочлен Ньютона с разделенными разностями
- 32. 4.6. Интерполирование сплайнами Пусть на [a; b] задана сетка - множество полиномов степени m - множество
- 33. Функция называется полиномиальным сплайном степени m дефекта k с узлами если:
- 34. Пусть на [a; b] задана сетка и некоторые числа Говорят, что сплайн интерполирует функцию f(x) на
- 35. Узлы сетки - узлы сплайна Узлы сетки – узлы интерполяции Для сплайнов чётной степени Для сплайнов
- 36. Пример
- 43. Интерполяционным кубическим сплайном, соответствующим данной функции f(x), называется функция s(x), удовлетворяющая условиям:
- 47. 4.7. Метод наименьших квадратов y = F(x)
- 48. y = F(x, a, b, c) F(xi, a, b, c) = yi (i = 1, 2,...,n)
- 49. yi – F(xi, a, b, c) = εi (i = 1, 2,..., n)
- 50. F(x) = ax + b (*)
- 52. ln F(x) = ln a + mln x в таблице логарифмируем все значения xi и yi
- 53. ln F(x) = ln a + mx В таблице логарифмируем только значения yi , находим параметры
- 54. В таблице все значения yi заменяются на обратные, xi остаются без изменения. Параметры a и b
- 55. Все значения xi заменяются на обратные, а yi остаются без изменения. Параметры a и b находятся
- 56. Все значения xi и yi заменяются на обратные. Параметры a и b находятся из системы (*)
- 57. Логарифмируем только значения xi. Параметры a и b находятся из системы (*)
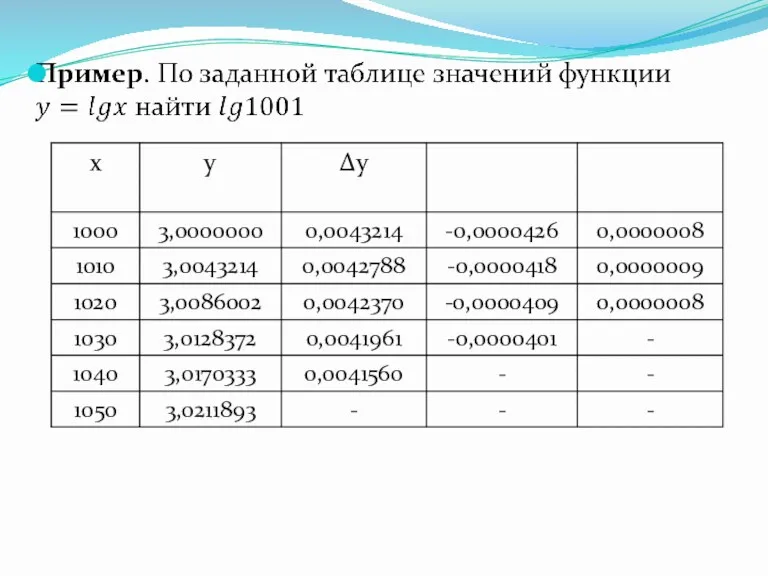
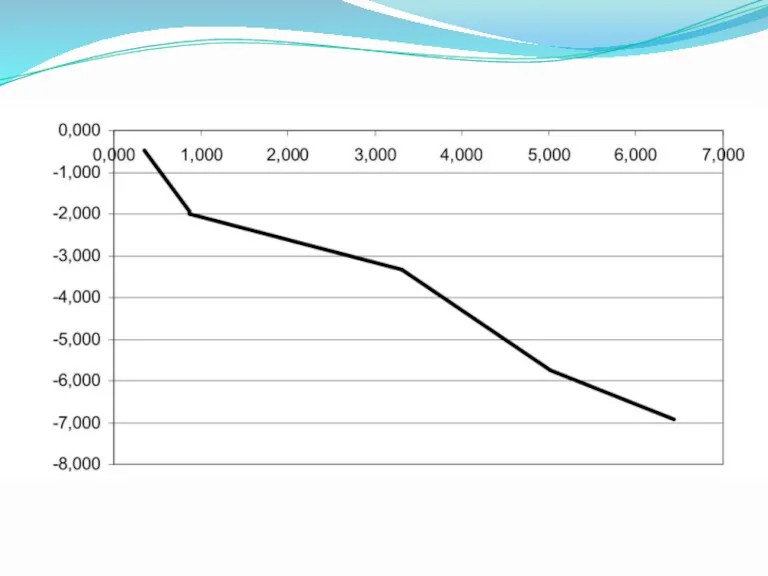
- 58. Пример. По заданной таблице значений x и y найти методом наименьших квадратов эмпирическую формулу F(x) =
- 60. Скачать презентацию













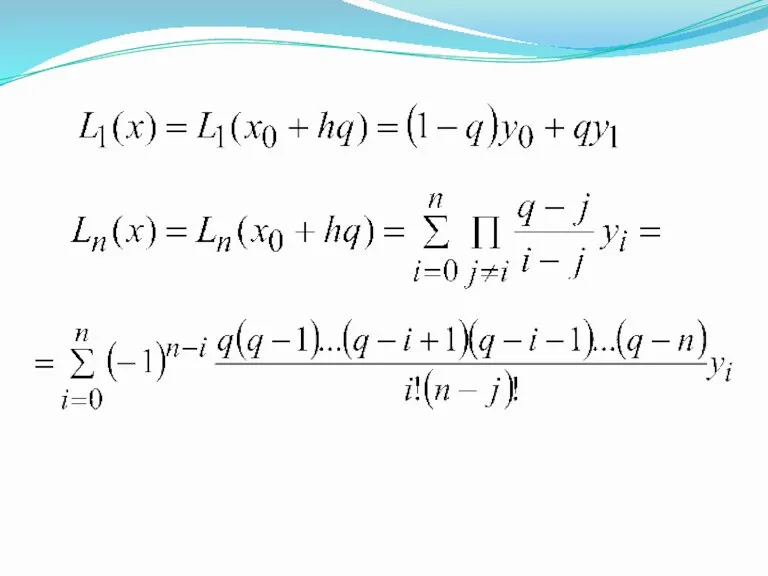














![4.6. Интерполирование сплайнами Пусть на [a; b] задана сетка -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/434065/slide-31.jpg)

![Пусть на [a; b] задана сетка и некоторые числа Говорят,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/434065/slide-33.jpg)













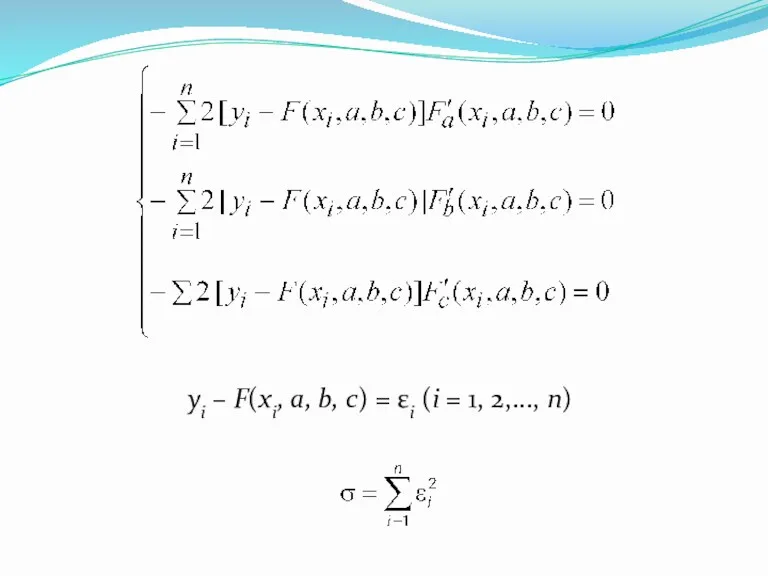









 Интегрированный урок История и математика (6 класс)
Интегрированный урок История и математика (6 класс)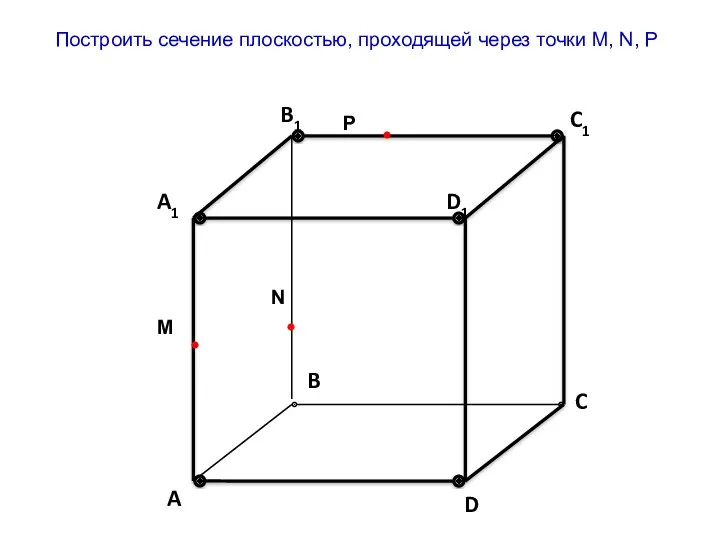 Построение сечения плоскостью
Построение сечения плоскостью Методы кибернетики
Методы кибернетики Параллелепипед. Геометрия. 10 класс
Параллелепипед. Геометрия. 10 класс Приёмы устных вычислений вида 100 разд. на 50
Приёмы устных вычислений вида 100 разд. на 50 Тригонометрия
Тригонометрия Числовой набор
Числовой набор Дифференциал функции
Дифференциал функции Дискретные структуы. Теория графов. Основные понятия
Дискретные структуы. Теория графов. Основные понятия Сучасні методи наближення функцій багатьох змінних (інтерлінація)
Сучасні методи наближення функцій багатьох змінних (інтерлінація) Обучение детей измерению с помощью общепринятыхединиц измерения: см, дм, м
Обучение детей измерению с помощью общепринятыхединиц измерения: см, дм, м Координатна пряма. Математика. 6 клас
Координатна пряма. Математика. 6 клас Десятичная запись дробей
Десятичная запись дробей Параллельные прямые и секущие. Задания для устного счета. Упражнение 8. 7 класс
Параллельные прямые и секущие. Задания для устного счета. Упражнение 8. 7 класс Умножение десятичных дробей
Умножение десятичных дробей Формулы сложения
Формулы сложения ОГЭ 2016. Модуль Алгебра №2
ОГЭ 2016. Модуль Алгебра №2 Descriptive statistics. Frequency distributions and their graphs. (Section 2.1)
Descriptive statistics. Frequency distributions and their graphs. (Section 2.1) Анализ одномерных распределений
Анализ одномерных распределений Метод анализа иерархий (МАИ)
Метод анализа иерархий (МАИ) Экспоненциальные методы для анализа временных рядов
Экспоненциальные методы для анализа временных рядов Математика. 1 класс. Урок 95. Табличное сложение и вычитание - Презентация
Математика. 1 класс. Урок 95. Табличное сложение и вычитание - Презентация Алгебра и начала анализа 10 – 11 класс. Муравин Георгий Константинович, Муравина Ольга Викторовна
Алгебра и начала анализа 10 – 11 класс. Муравин Георгий Константинович, Муравина Ольга Викторовна Развёртка прямоугольного параллелепипеда. Урок 143
Развёртка прямоугольного параллелепипеда. Урок 143 Длина окружности и площадь круга
Длина окружности и площадь круга Свойства прямой и обратной функций
Свойства прямой и обратной функций Системы с нечеткой логикой. Лекция 21-22
Системы с нечеткой логикой. Лекция 21-22 Математическое моделирование. Движение по градиенту
Математическое моделирование. Движение по градиенту