Содержание
- 2. Преподаватель – Терехова Екатерина Олеговна Katerin.terekhova@gmail.com terekhova.e.o@muctr.ru https://vk.com/terekhova_kate 8-906-758-54-10 (Telegram, What’s app) Каб. 523 5 этаж
- 3. Конспекты лекций размещены на сайте (*.pdf): http://quant.hostronavt.ru/ Внимание! На экзамене/зачете можно пользоваться распечатками конспектов лекций, своими
- 4. Учебные пособия: Цирельсон В.Г., Бобров М.Ф. «Многоэлектронный атом». 2. Цирельсон В.Г. , Бобров М.Ф. «Квантовая химия
- 5. Организационные моменты Рейтинговая система. Максимальное количество баллов: весь курс – 100. экзамен или зачет – 40
- 6. Часть 1. Что такое квантовая химия и в чем ее особенности? Физика, немного математики и капелька
- 7. Зачем изучать квантовую химию? Квантовая химия – наука, использующая методы квантовой механики для описания химических явлений.
- 8. Что такое химический элемент? совокупность атомов с одинаковым зарядом ядра и числом протонов, совпадающим с порядковым
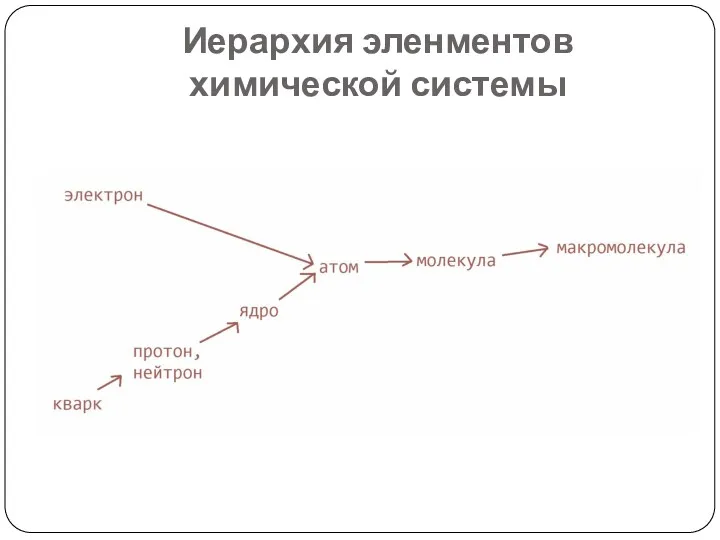
- 9. Иерархия эленментов химической системы
- 10. Квантово-волновой дуализм материальных объектов природы Макс Планк М. Планк вывел формулу для энергии излучения абсолютно черного
- 11. Луи Де Бройль В свое время, Де Бройль высказал идею о двойственной природе всех объектов природы.
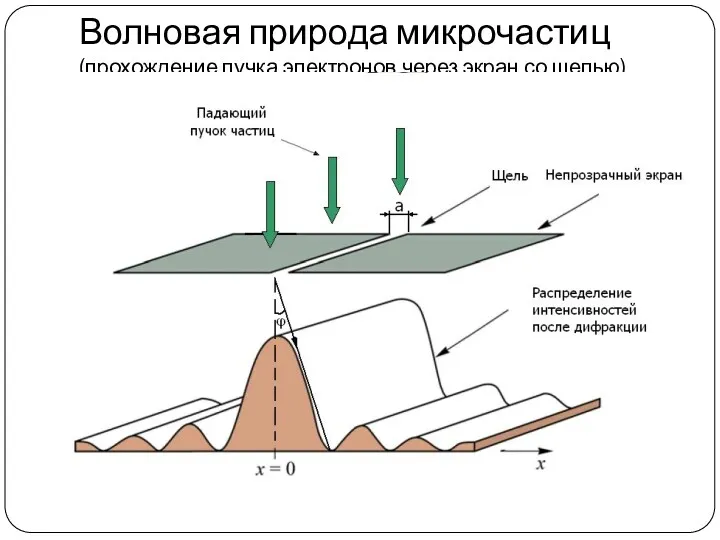
- 12. Волновая природа микрочастиц (прохождение пучка электронов через экран со щелью)
- 13. Макромир Координаты частиц, их скорости и законы их изменения полностью определяет всю эволюцию системы. Микромир Малые
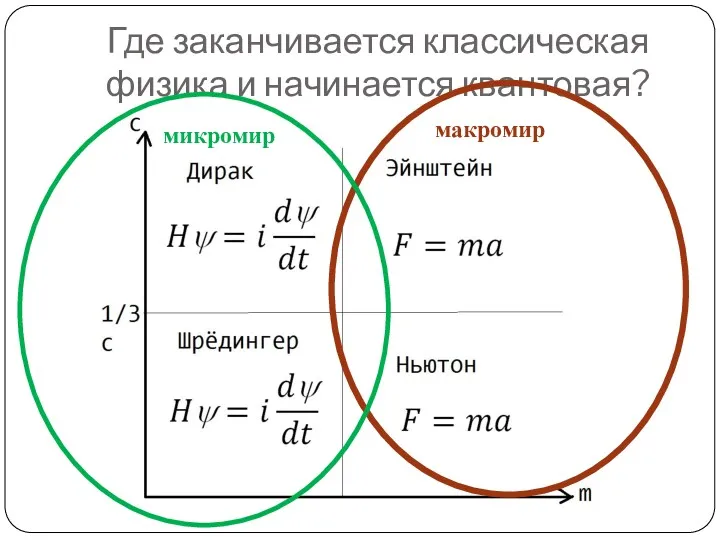
- 14. Где заканчивается классическая физика и начинается квантовая? микромир макромир
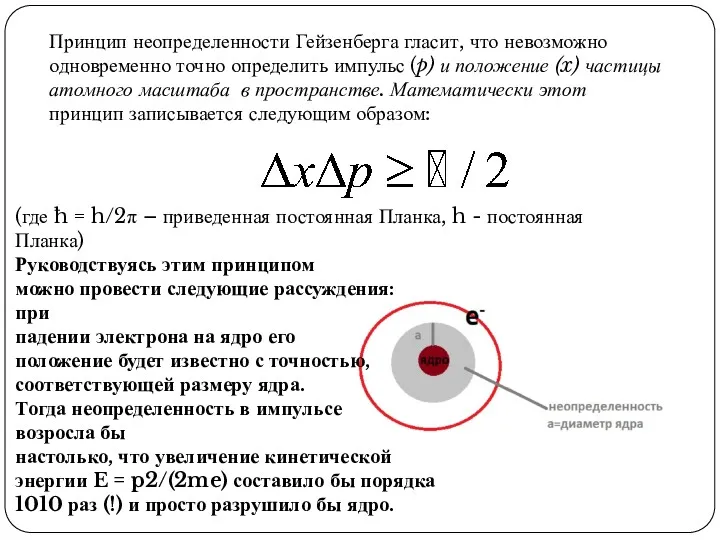
- 15. Принцип неопределенности Гейзенберга гласит, что невозможно одновременно точно определить импульс (p) и положение (x) частицы атомного
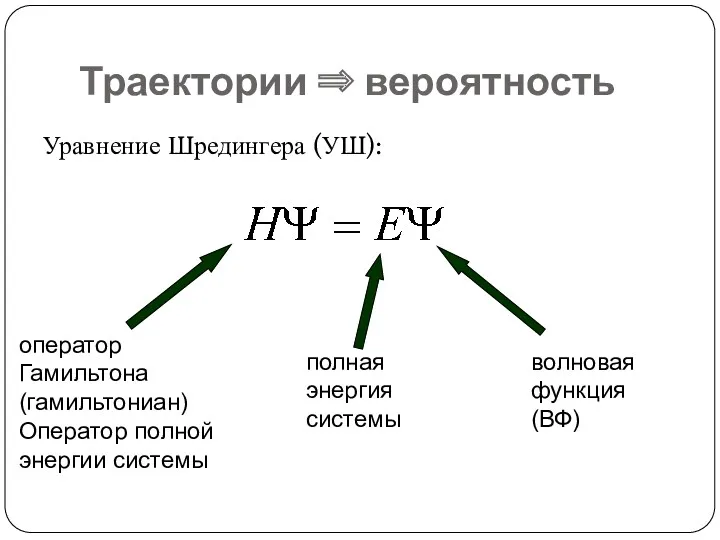
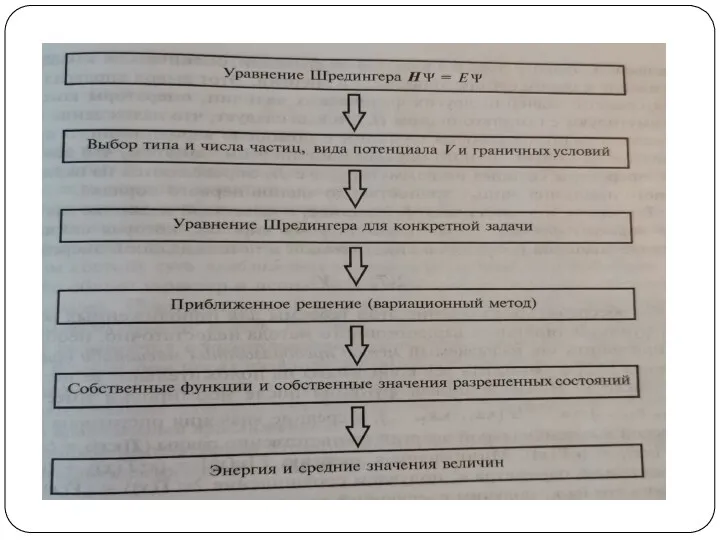
- 16. Траектории ⇒ вероятность Уравнение Шредингера (УШ): оператор Гамильтона (гамильтониан) Оператор полной энергии системы волновая функция (ВФ)
- 17. Основные постулаты квантовой механики Каждое состояние системы n частиц полностью описывается функцией координат частиц xi и
- 18. Волновая функция (ВФ) ВФ – функция координат всех частиц системы и времени: Если временной зависимости нет:
- 19. Требования к «идеальной» ВФ Непрерывна -электрон всегда существует и не может вдруг исчезнуть, затем вдруг появиться
- 20. Физический смысл ВФ ⎜Ψ(r)⎜2dV вероятность найти частицу в объеме dV вблизи точки r. ⎜Ψ(r)⎜2 плотность вероятности
- 21. 2. Каждой доступной измерению величине А в любом из возможных состояний соответствует линейный эрмитов оператор А.
- 22. Что такое оператор? В квантовой механике и квантовой химии, оператор – это линейное отображение (математическое правило),
- 23. В квантовой механике все операторы линейные, чтобы не нарушался принцип суперпозиции состояний (чтобы не было такого,
- 24. Что это за эрмитовы операторы? Такие операторы еще называют самосопряженными. Т.е. выполняется равенство: Выражение выше значит,
- 25. Эрмитовы операторы 1. Представляют собой квадратную матрицу – т.е. число строк всегда совпадает с числом столбцов
- 26. Эрмитово сопряжение Ранее было сказано, что для всех эрмитовых операторов выполняется равенство: + в данном случае
- 27. Что это за скобки дирака? В квантовой механике и в квантовой химии свой, достаточно специфичный математический
- 28. Еще немного математики Скобки дирака носят названия «бра» и «кет», от английского слова bracket – скобка.
- 29. Скалярное произведение векторов
- 30. 3. Независящая от времени волновая функция Ψ удовлетворяет стационарному уравнению Шредингера: HΨ = ЕΨ H=T+V -
- 31. Оператор кинетической энергии частицы кинетическая энергия в классической механике оператор кинетической энергии в квантовой механике
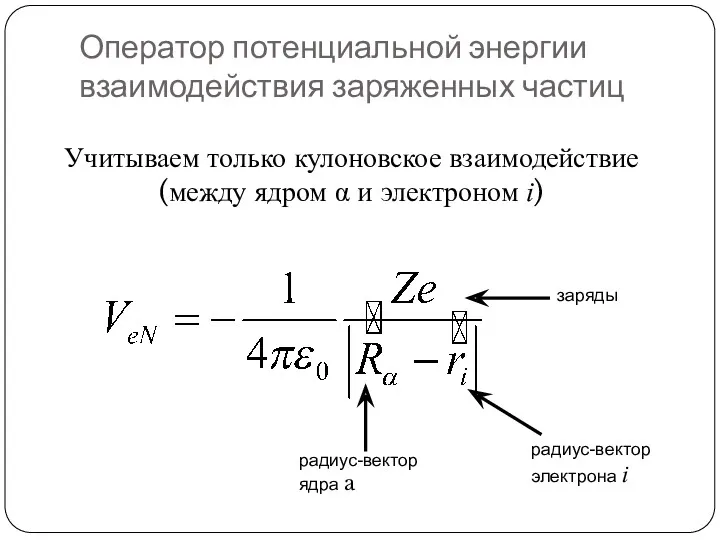
- 32. Оператор потенциальной энергии взаимодействия заряженных частиц Учитываем только кулоновское взаимодействие (между ядром α и электроном i)
- 33. 4. Все одинаковые частицы тождественны. Именно поэтому можно говорить о неразличимости электронов: замена одного из них
- 34. 5. Значения величины А, которые могут быть измерены, являются собственными значениями аi уравнения на собственные значения
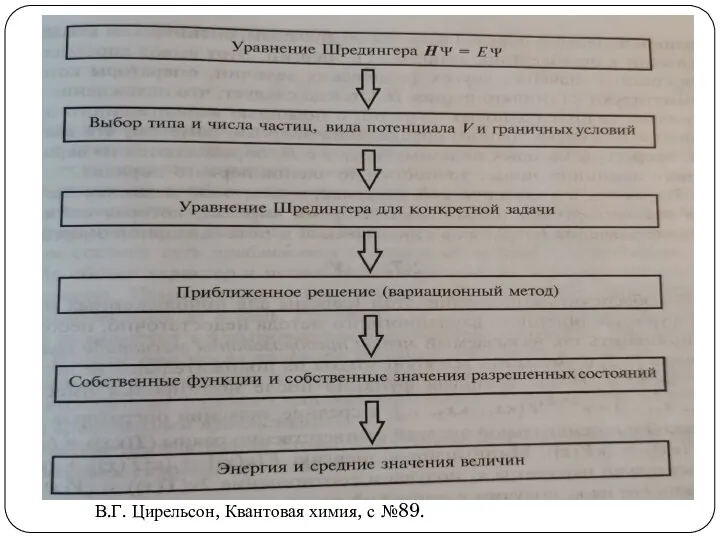
- 35. Иначе: решение уравнения Шредингера есть не что иное, как решение задачи на собственные значения для оператора
- 36. 6. Среднее значение величины А для системы, находящейся в состоянии i, определяется выражением (предполагается, что волновые
- 37. где wi - вероятность пребывания системы в состоянии i, Принцип суперпозиции состояний дает рецепт определения измеряемых
- 39. Часть 2. Атом водорода Уже больше химии с капелькой математики и физики.
- 40. Эрвин Шредингер Уравнение Шредингера Волновая функция зависит от координат электрона. Она не имеет физического смысла Физический
- 41. Глобально, в квантовой химии все методы и задачи направлены на решение одной глобальной проблемы – решить
- 42. Вариационный принцип Любая система стремится занять состояние с минимальной энергией (всякая система хочет быть стабильной) Вариационный
- 43. Док-во: Среднее значение оператора Н для приближенной волновой функции Ψ, нормированной на 1 : Разложим Ψ
- 44. На языке вариационного исчисления условие минимума эквивалентно требованию обращения в нуль первой вариации среднего значения Н:
- 45. - матричные элементы оператора Н в базисе функций Sij - элементы матрицы интегралов перекрывания, вычисленной c
- 46. Приравняем нулю определитель (детерминант) из коэффициентов при ci : или вековое или секулярное уравнение При разложении
- 47. В.Г. Цирельсон, Квантовая химия, с №89.
- 48. Состояние атома водорода полностью определяется волновой функцией, зависящей только от координат электрона. Гамильтониан атома Н: движение
- 49. Операторы T и V: разные системы координат. Электрон в атоме Н – пример центрального поля, сила
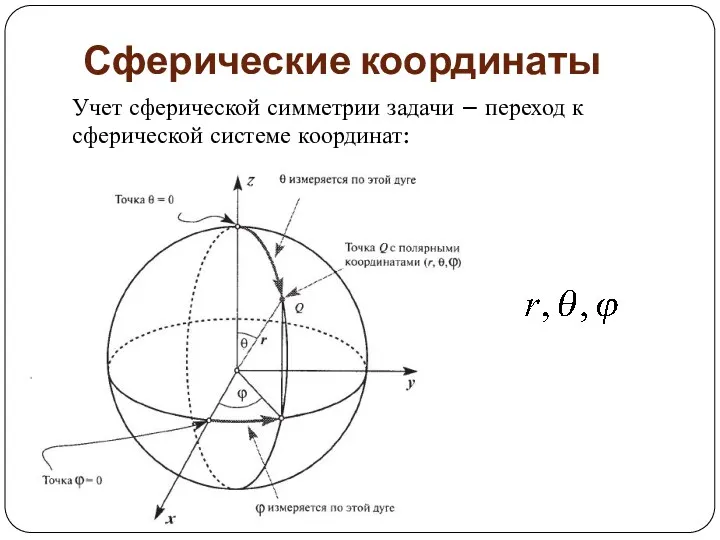
- 50. Сферические координаты Учет сферической симметрии задачи – переход к сферической системе координат:
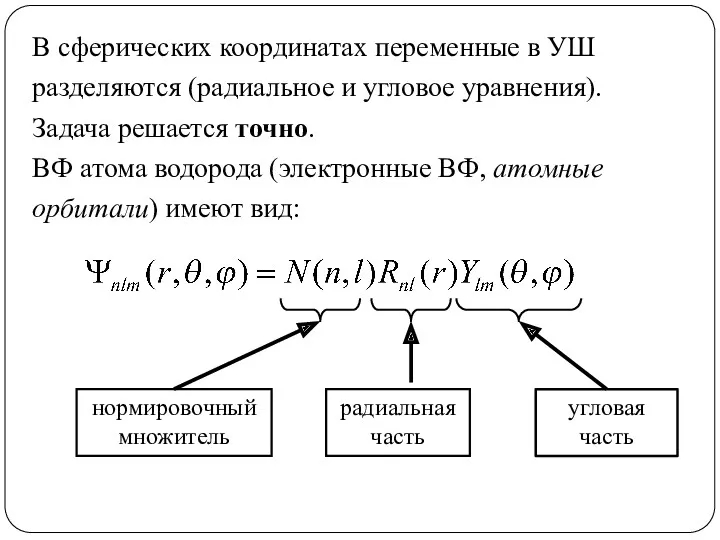
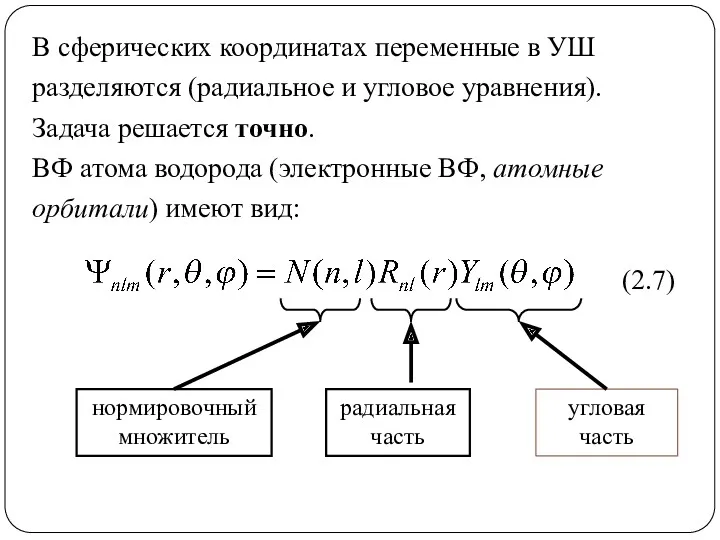
- 51. В сферических координатах переменные в УШ разделяются (радиальное и угловое уравнения). Задача решается точно. ВФ атома
- 52. Радиальная часть ВФ водородоподобных атомов N – нормировочный множитель, L – присоединенные полиномы Лягерра, Z –
- 53. Угловые функции Угловые функции Ylm(θ, ϕ) описывают в сферических координатах (θ, ϕ) угловую зависимость вероятностного распределения
- 54. n – главное, l – орбитальное, m – магнитное квантовые числа. Уравнение Шредингера с гамильтонианом имеет
- 55. Квантовые числа Три квантовых числа согласно УШ определяют состояние атома водорода: 1. n =1, 2, 3...
- 56. n – главное квантовое число, характеризующее полную энергию электрона на n оболочке, определяет размер орбитали L-определяет
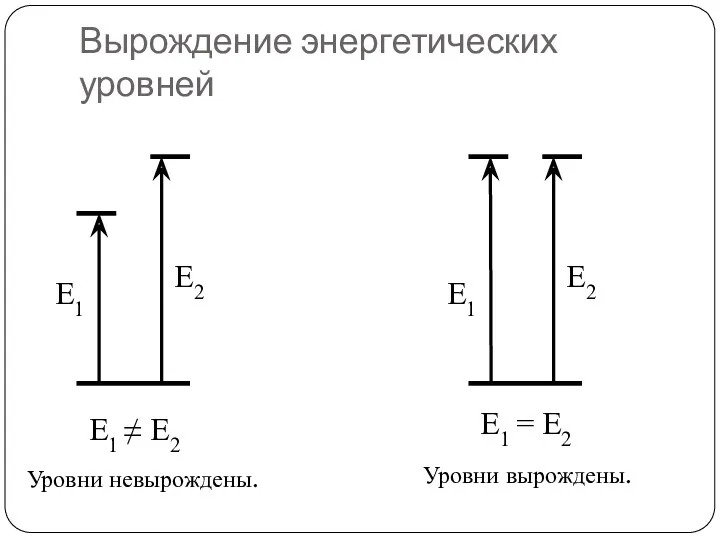
- 57. Вырождение энергетических уровней E1 E2 E1 E2 E1 ≠ E2 E1 = E2 Уровни невырождены. Уровни
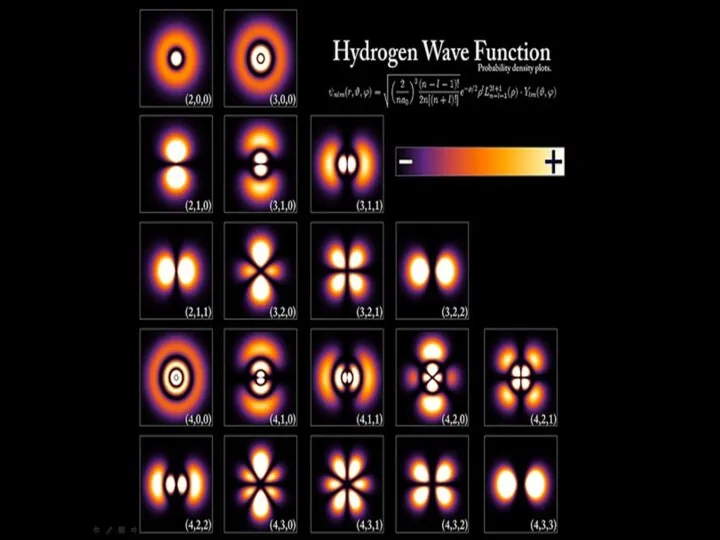
- 58. Атом водорода – простая реальная система В результате решения уравнения Шредингера для атома водорода возникают квантовые
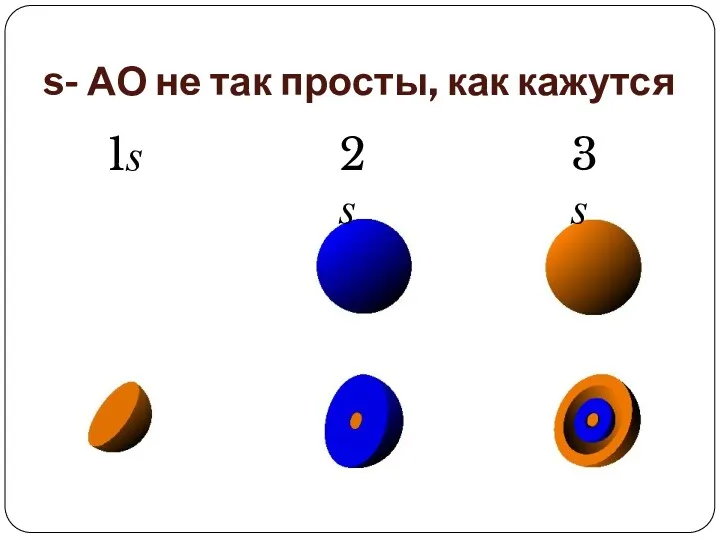
- 60. s- АО не так просты, как кажутся 1s 2s 3s
- 61. Спектральные линии Спектр поглощения водорода Спектр испускания водорода
- 62. Спектральные линии атома H
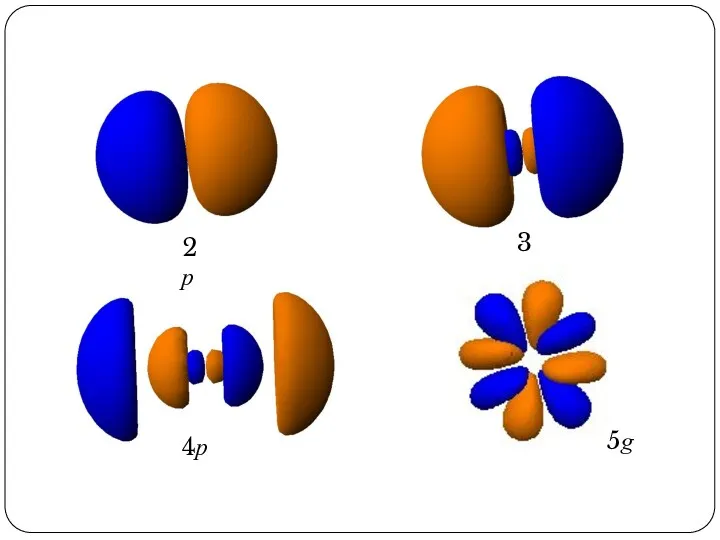
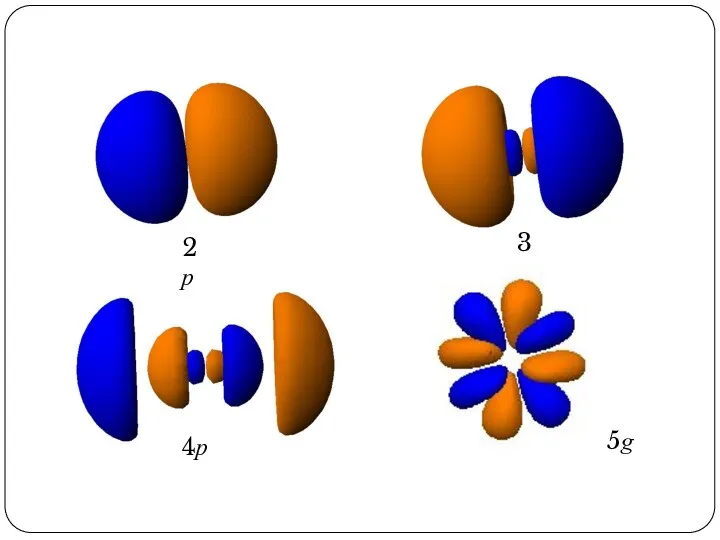
- 63. 2p 3p 4p 5g
- 64. Система СИ Система Хартри
- 65. Расчетные задания и примеры Часть 3. Радиальная и угловая ВФ
- 66. В сферических координатах переменные в УШ разделяются (радиальное и угловое уравнения). Задача решается точно. ВФ атома
- 67. Радиальная часть ВФ водородоподобных атомов N – нормировочный множитель, L – присоединенные полиномы Лягерра, Z –
- 68. Нормированные радиальные функции атома водорода Rnl (Z = 1, система СИ)
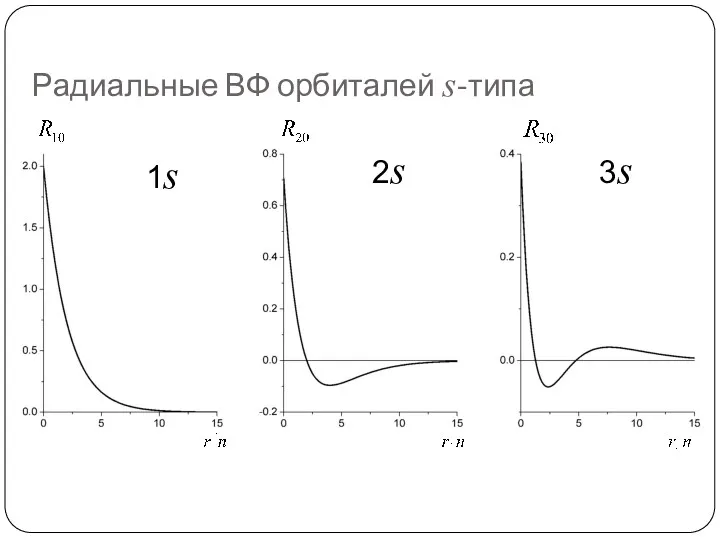
- 69. Радиальные ВФ орбиталей s-типа 1s 2s 3s
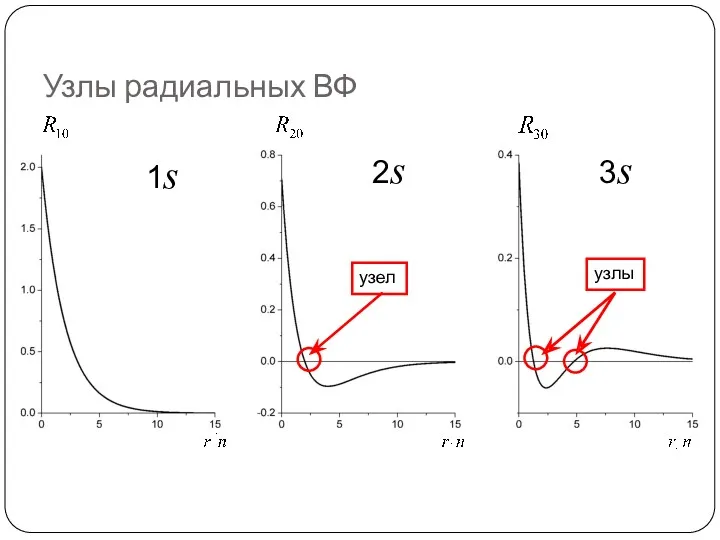
- 70. Узлы радиальных ВФ 1s 2s 3s узел узлы
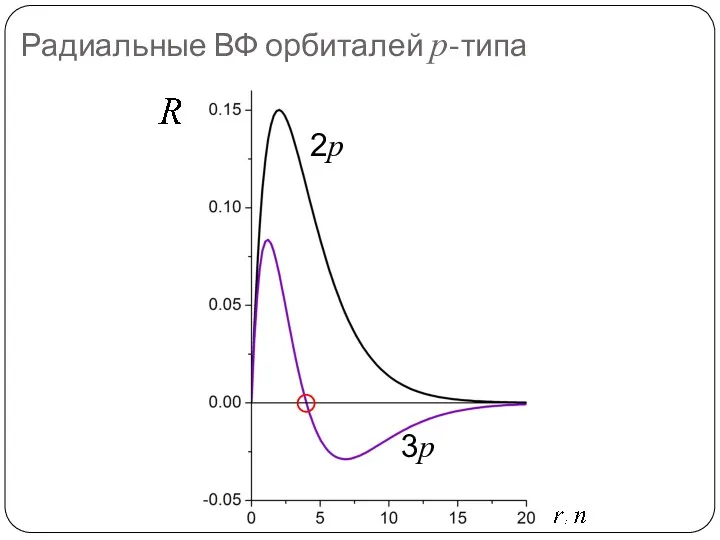
- 71. Радиальные ВФ орбиталей p-типа 2p 3p
- 72. Сколько узлов у радиальной части ВФ? Число узлов = n – l – 1 Откуда узлы
- 73. s- АО не так просты, как кажутся 1s 2s 3s
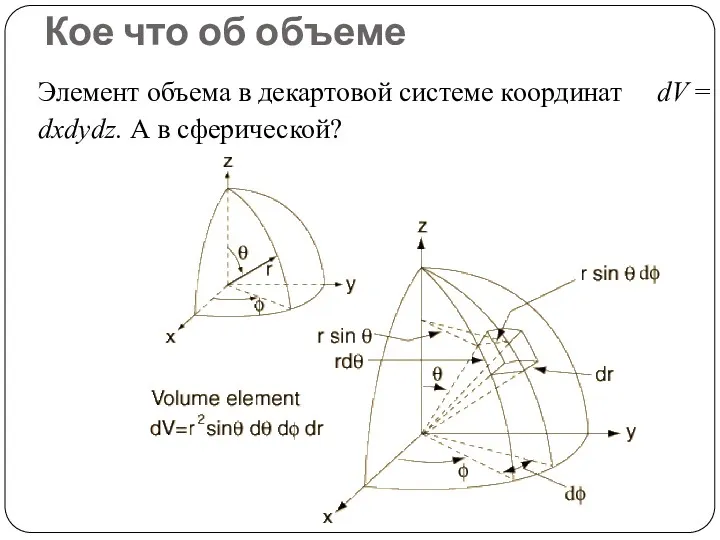
- 74. Кое что об объеме Элемент объема в декартовой системе координат dV = dxdydz. А в сферической?
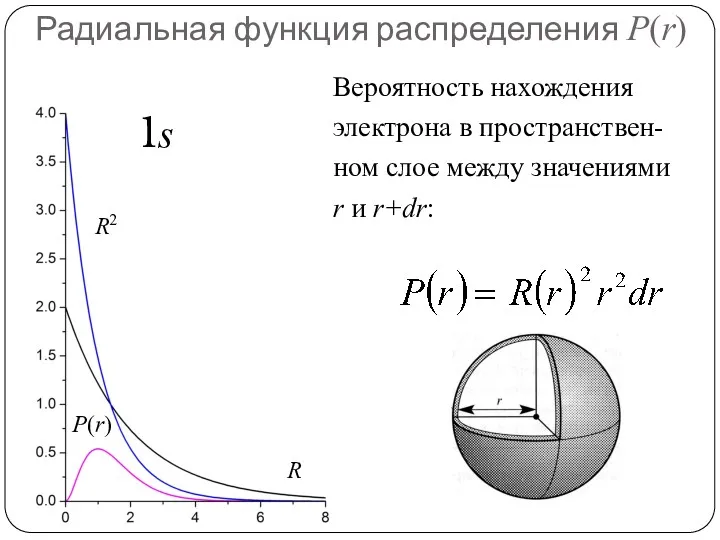
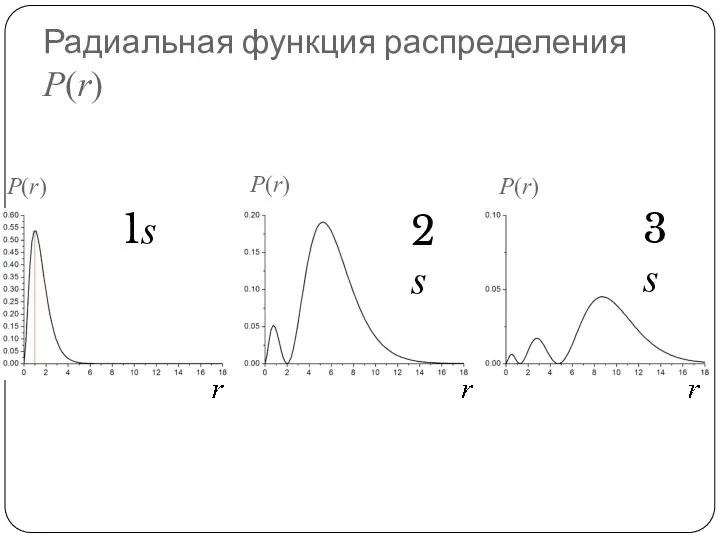
- 75. Радиальная функция распределения P(r) Её можно получить, проинтегрировав по угловым переменным θ и ϕ. Отметим, что
- 76. Радиальная функция распределения P(r) Вероятность нахождения электрона в пространствен-ном слое между значениями r и r+dr:
- 77. Наиболее вероятное положение электрона на орбитали Приравнивая нулю производную Pnl по r, можно найти наиболее вероятное
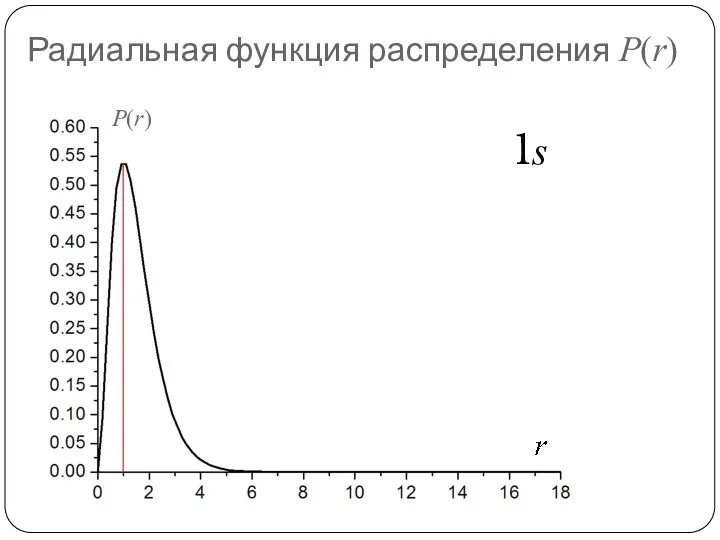
- 78. Радиальная функция распределения P(r)
- 79. Радиальная функция распределения P(r)
- 80. Угловые функции Угловые функции Ylm(θ, ϕ) описывают в сферических координатах (θ, ϕ) угловую зависимость вероятностного распределения
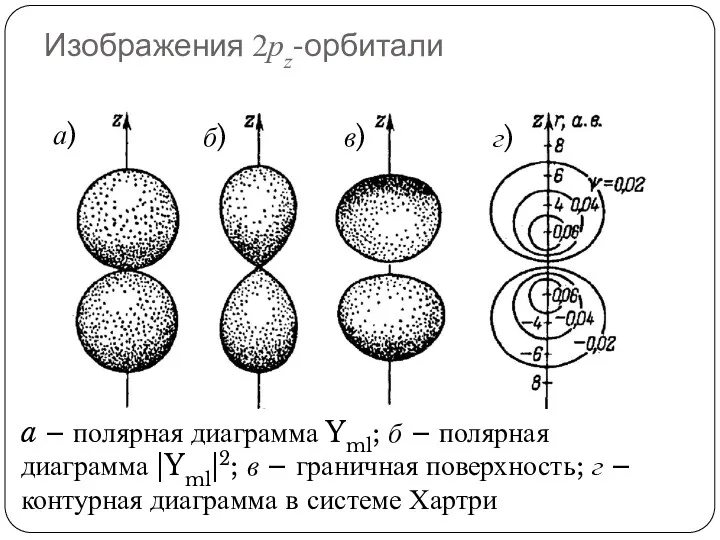
- 81. Изображения 2pz-орбитали a – полярная диаграмма Yml; б – полярная диаграмма |Yml|2; в – граничная поверхность;
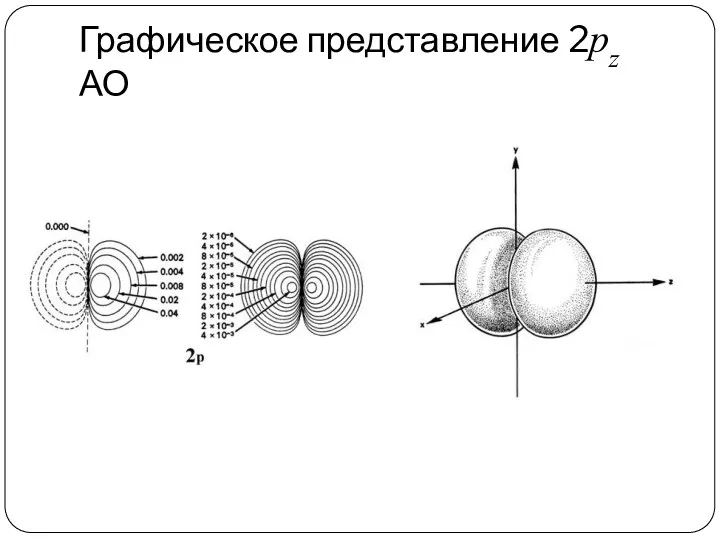
- 82. Графическое представление 2рz АО
- 83. Число узловых поверхностей у угловой составляющей ВФ Число узловых поверхностей = l
- 84. 2p 3p 4p 5g
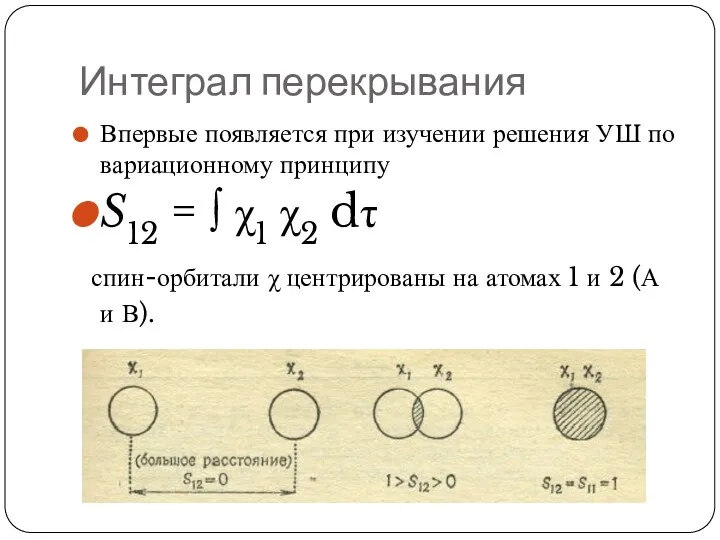
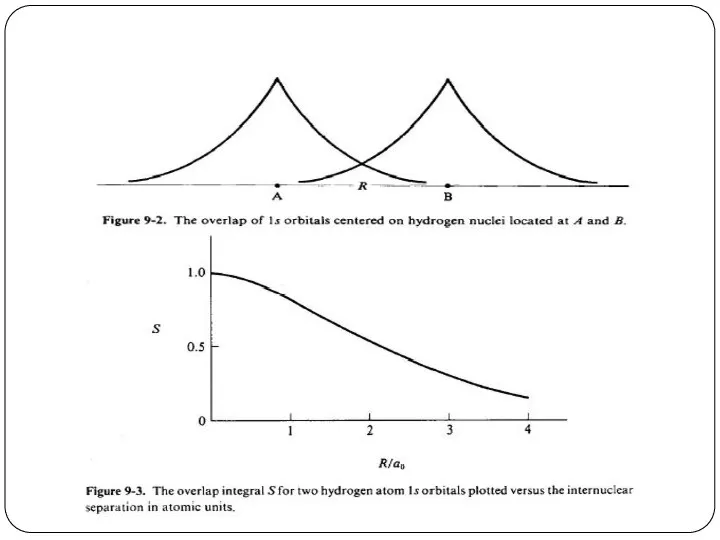
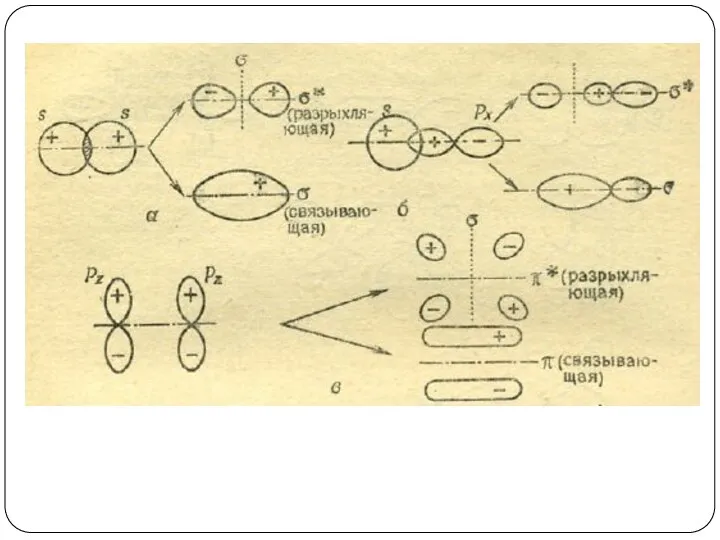
- 85. Интеграл перекрывания Впервые появляется при изучении решения УШ по вариационному принципу S12 = ∫ χ1 χ2
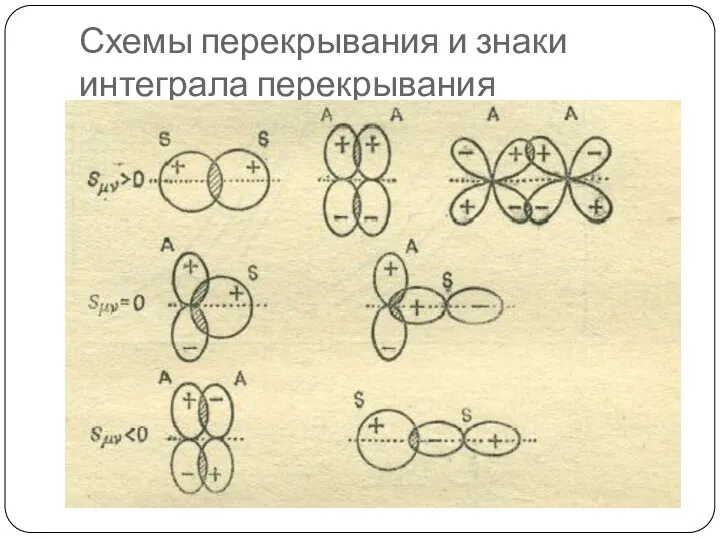
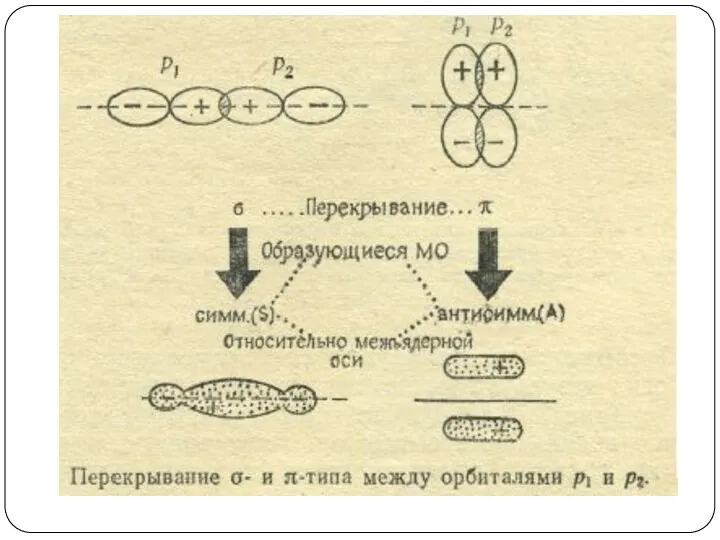
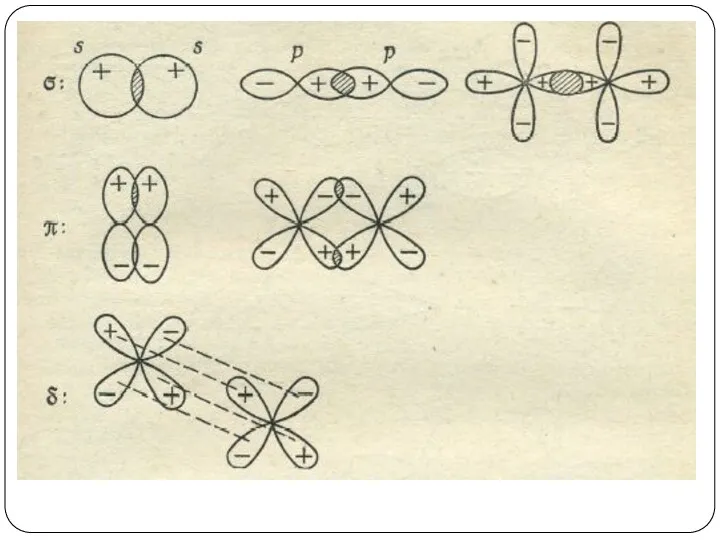
- 87. Схемы перекрывания и знаки интеграла перекрывания
- 91. Зависимость интеграла перекрывания некоторых типов связи от межъядерного расстояния
- 92. Кратко Часть 4. Неэмпирические методы расчета. Основные приближения
- 93. Вариационный принцип Приближенный метод решения УШ Минимизация энергии «Основа» для дальнейших методов решения УШ
- 95. Одноэлектронное приближение (приближение независимых частиц) Электроны неразличимы Электрон i имеет энергию ei и его состояние описывается
- 96. Для того, чтобы провести усреднение , надо уже знать функции, описывающие электроны j ≠ i! Как
- 97. и строят оператор (h0i)ССП. Затем решают набор одноэлектронных уравнений Хартри. Полученные решения χ1j(rj) используют, чтобы построить
- 98. ССП (метод Хартри) Межэлектронным отталкиванием не пренебрегают, но действие на каждый электрон всех остальных электронов заменяют
- 99. ЦП Поправка на атом водорода «Форма» того самого поля
- 100. Детерминант Слейтера Электроны обладают собственным моментом количества движения (спином), который в единицах ħ равен ±. Чтобы
- 101. Заполнение электронами состояний любого атома происходит в порядке возрастания их энергий согласно принципа Паули и каждое
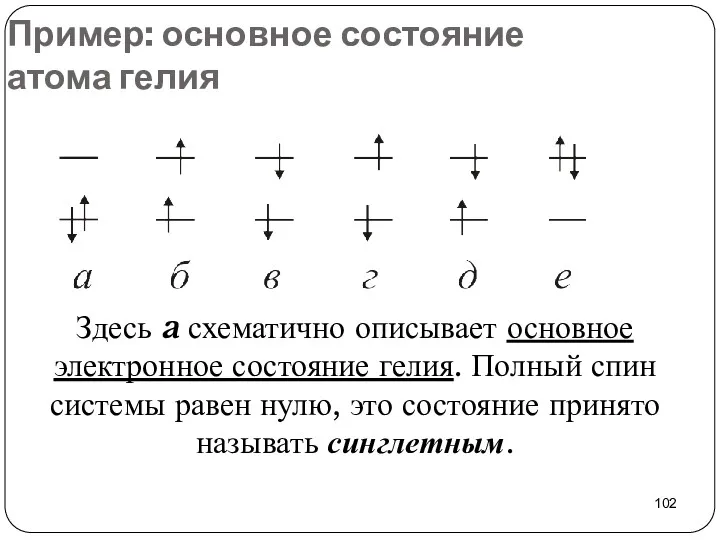
- 102. Пример: основное состояние атома гелия Здесь a схематично описывает основное электронное состояние гелия. Полный спин системы
- 103. Состояния и соответствующие им АО с одинаковыми квантовыми числами n и l заполняются так, чтобы суммарный
- 104. . Пример: атом гелия (2 электрона). Две эквивалентных волновых функции Хартри для этой системы имеют вид:
- 105. антисимметрична ( – нормировочный коэффициент). Если мы попытаемся поместить электроны 1 и 2 на одну и
- 106. С математической точки зрения волновая функция есть детерминант из спин-орбиталей χi(х): . Важным свойством детерминанта является
- 107. Принцип Паули диктует, что две спин-орбитали с одинаковыми пространственными частями (т.е. с одинаковыми n, l, m)
- 108. Волновая функция основного состояния атома He: где функция Функция имеет симметричную пространственную часть и антисимметричную спиновую.
- 109. Антисимметричная полная ВФ – детерминант Слэтера Спин-орбитали электроны
- 110. . Детерминант Слейтера - единственная функция, обеспечивающая антисимметричность волновой функции, записанной через орбитали (орбитальное приближение). Следовательно,
- 111. . Системы, в которых все электроны занимают орбитали попарно, называются системами с закрытыми (замкнутыми) электронными оболочками.
- 112. Приближение Борна-Оппенгеймера Решение стационарного уравнения Шредингера для многоатомных молекул − очень сложная задача. Поэтому в квантовой
- 113. Это позволяет заменить стационарное уравнение Шредингера (УШ) двумя другими уравнениями, которые решаются последовательно. На первом этапе
- 114. На втором этапе решают ядерное УШ: [Tя + U(R)]Ψяд(R) = ЕΨяд(R) Tя - кинетическая энергия ядер.
- 115. Метод Хартри-Фока Вместо привычного нам оператора гамильтона Н появляется оператор Фока F (фокиан). Фокиан – это
- 116. Недостатки метода Хартри-Фока-(Рутана) Взаимодействие между электронами рассчитывается приближенно (вводится эффективный потенциал). Электроны движутся независимо друг от
- 117. Метод Хартри-Фока для молекул Приближение Борна-Оппенгеймера ⇒ ядерная геометрия фиксирована Волновая функция – детерминант Слэтера, составленный
- 118. Приближение МО ЛКАО Молекулярная Орбиталь – Линейная Комбинация Атомных Орбиталей: M атомных орбиталей (АО) χμ называются
- 119. Что это такое, зачем это нужно, как считать, а также, почем нельзя обойтись без них Часть
- 120. Мы много говорили об орбиталях и ВФ, которые их описывают. Возникает вопрос: а как выглядят эти
- 121. Выбор базисных АО χ Должны давать хорошее приближение к истинной ВФ (например, возле ядер и на
- 122. АО состоит из угловой и радиальной частей. В качестве угловой части используются сферические гармоники Ylm –
- 123. OCT (STO) – орбитали Слейтеровского типа Функции STO – точные решения для радиальных частей орбиталей водородоподобного
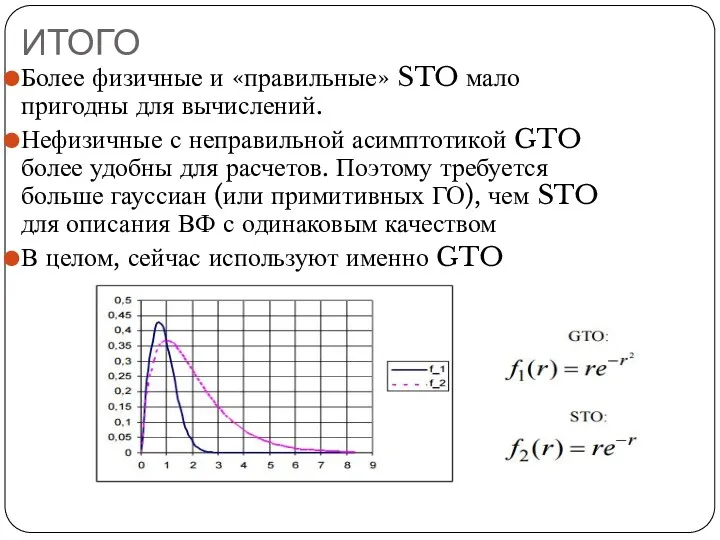
- 124. ИТОГО Более физичные и «правильные» STO мало пригодны для вычислений. Нефизичные с неправильной асимптотикой GTO более
- 125. Номенклатура базисных наборов STO-nG Пытаемся с помощью GTO описать STO. Отсюда обозначения STO-nG. n – число
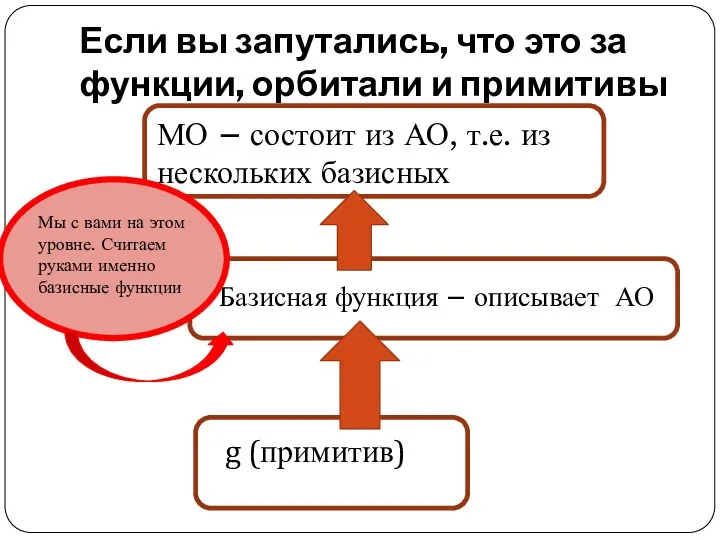
- 126. Если вы запутались, что это за функции, орбитали и примитивы g (примитив) Базисная функция – описывает
- 127. Минимальный базисный набор Тут все просто -одна функция на пару электронов остова и одна функцию на
- 129. Скачать презентацию
















































































![На втором этапе решают ядерное УШ: [Tя + U(R)]Ψяд(R) =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/179145/slide-113.jpg)











 Биогенді (s.p.d) элементтермен олардың қосылыстарының медициналық және биологиялық маңызы
Биогенді (s.p.d) элементтермен олардың қосылыстарының медициналық және биологиялық маңызы Кислоты, их состав и названия
Кислоты, их состав и названия Карбоновые кислоты и их функциональные производные
Карбоновые кислоты и их функциональные производные Ароматические углеводороды
Ароматические углеводороды Гетерофазный катализ. (Лекция 20)
Гетерофазный катализ. (Лекция 20) Горение топлива
Горение топлива Використання радіоактивних ізотопів, як індикаторів у тваринництві і археології
Використання радіоактивних ізотопів, як індикаторів у тваринництві і археології Основные классы неорганических соединений
Основные классы неорганических соединений Соли, их классификация и свойства
Соли, их классификация и свойства Органічна хімія
Органічна хімія Розв’язування задач за рівняннями реакцій з використанням розчинів із певною масовою часткою розчиненої речовини. Урок 13-14
Розв’язування задач за рівняннями реакцій з використанням розчинів із певною масовою часткою розчиненої речовини. Урок 13-14 Жёсткость воды
Жёсткость воды Полисахариды: крахмал и целлюлоза
Полисахариды: крахмал и целлюлоза Растворы. Часть 2. Лекция №7
Растворы. Часть 2. Лекция №7 Химия атмосферы. Химические процессы в тропосфере
Химия атмосферы. Химические процессы в тропосфере Буферные системы
Буферные системы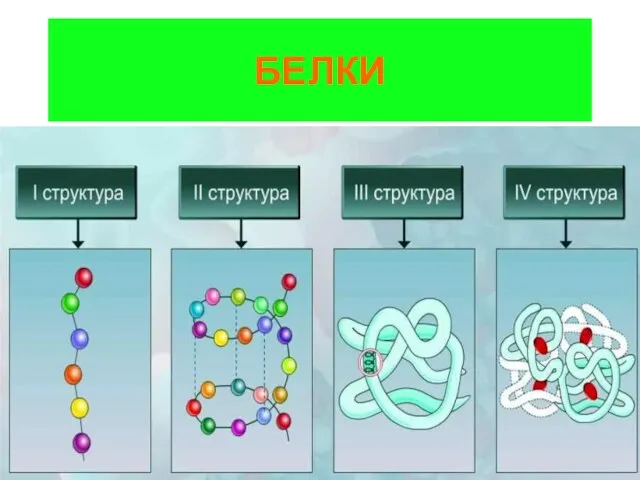 Белки. Строение
Белки. Строение Классификация химических элементов. Составитель. 8 класс
Классификация химических элементов. Составитель. 8 класс Минералы для ИЗБ
Минералы для ИЗБ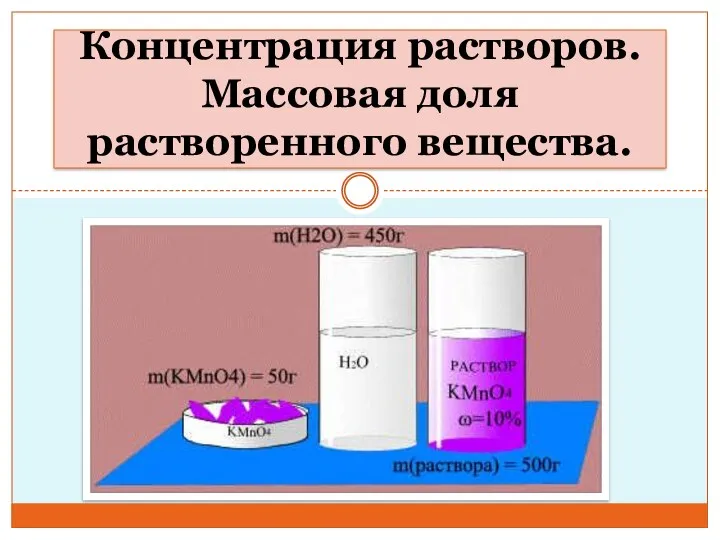 Концентрация растворов. Массовая доля растворенного вещества. Урок 1
Концентрация растворов. Массовая доля растворенного вещества. Урок 1 Химический элемент медь
Химический элемент медь Кинетика химических реакций
Кинетика химических реакций Кремний и его соединения
Кремний и его соединения Галогены. Расположите галогены в порядке их открытия
Галогены. Расположите галогены в порядке их открытия Важнейшие реакции в органической химии
Важнейшие реакции в органической химии Технология производства аминоальдегидных смол
Технология производства аминоальдегидных смол Углерод. Физические и химические свойства
Углерод. Физические и химические свойства Гидролиз солей
Гидролиз солей