Содержание
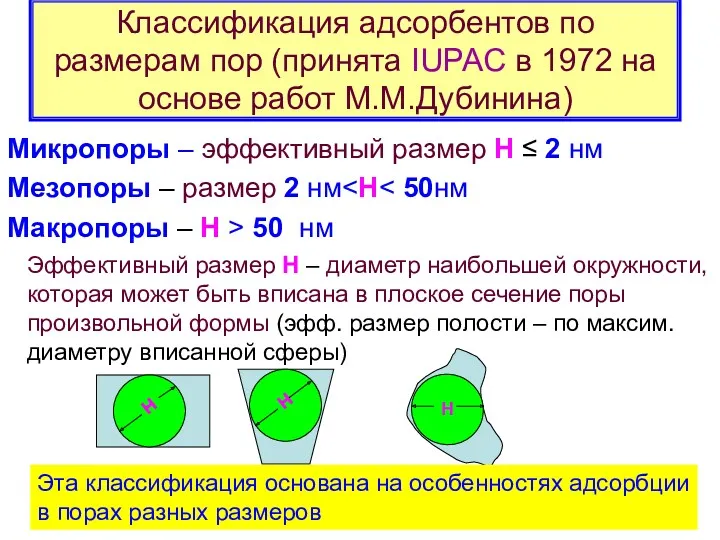
- 2. Классификация адсорбентов по размерам пор (принята IUPAC в 1972 на основе работ М.М.Дубинина) Микропоры – эффективный
- 3. В микропорах потенциал адсорбции повышен из-за сложения дисперсионных потенциалов близко расположенных стенок пор. Поэтому такие поры
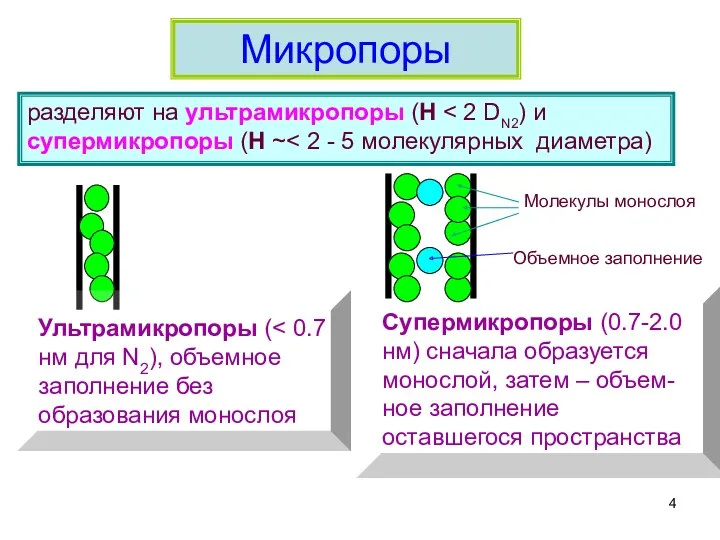
- 4. Микропоры
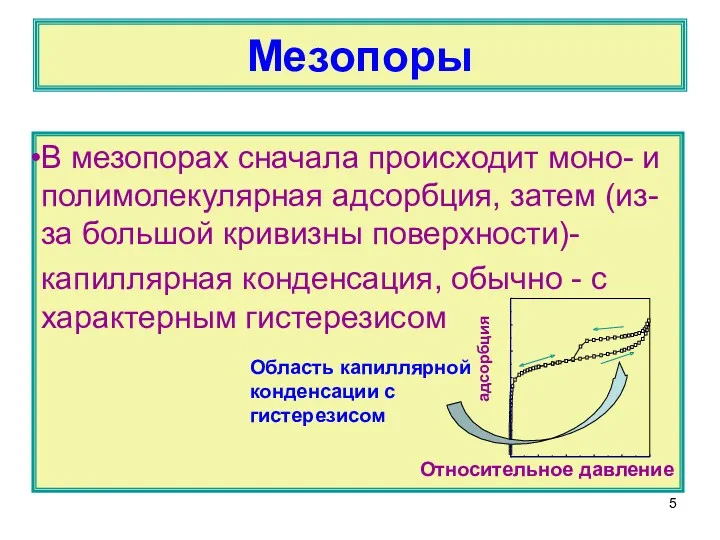
- 5. Мезопоры В мезопорах сначала происходит моно- и полимолекулярная адсорбция, затем (из-за большой кривизны поверхности)- капиллярная конденсация,
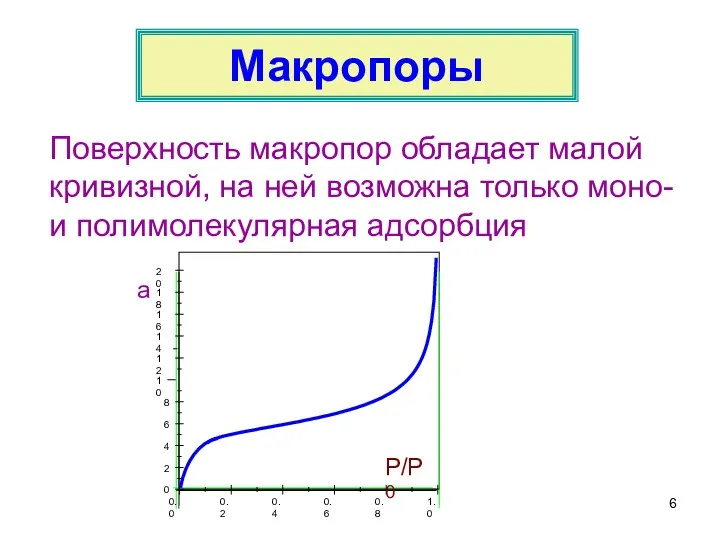
- 6. Поверхность макропор обладает малой кривизной, на ней возможна только моно- и полимолекулярная адсорбция Макропоры
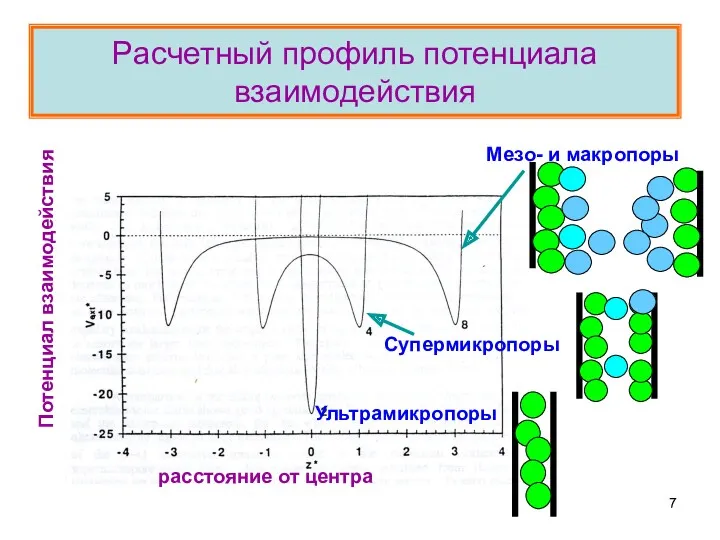
- 7. Pасчетный профиль потенциала взаимодействия
- 8. Расчет удельной поверхности по адсорбционным измерениям Наиболее распространенным является метод БЭТ (обычно – область Р/Р0 0.05-
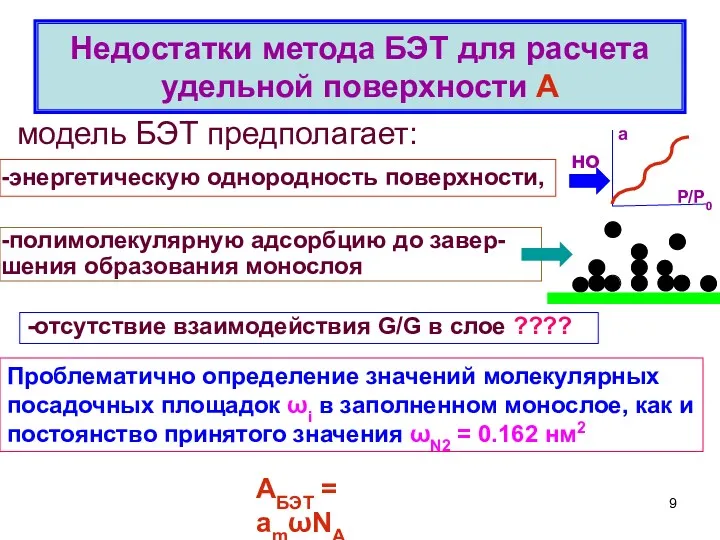
- 9. Недостатки метода БЭТ для расчета удельной поверхности А Проблематично определение значений молекулярных посадочных площадок ωi в
- 10. Создание альтернативных моделей адсорбции; Поиск более корректных методов расчета ω; Поиск методов, не использующих значения ω;
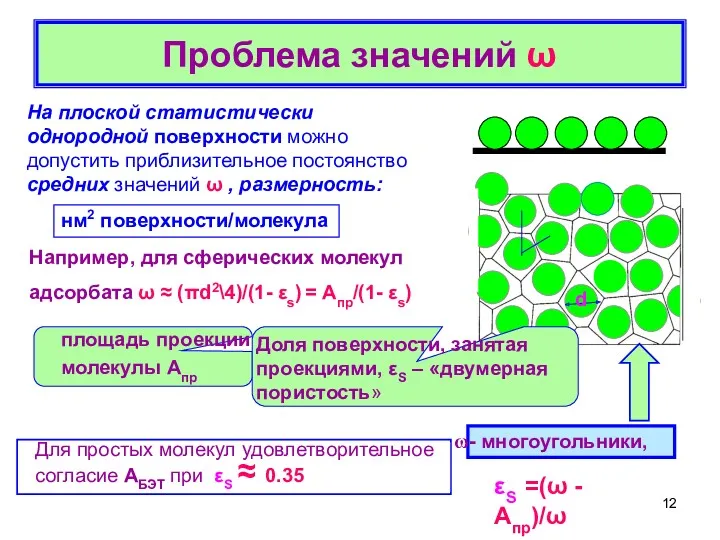
- 11. Проблема значений ω Одна из наиболее острых проблем связана с определением значений ω, которые необхо-димы для
- 12. Проблема значений ω
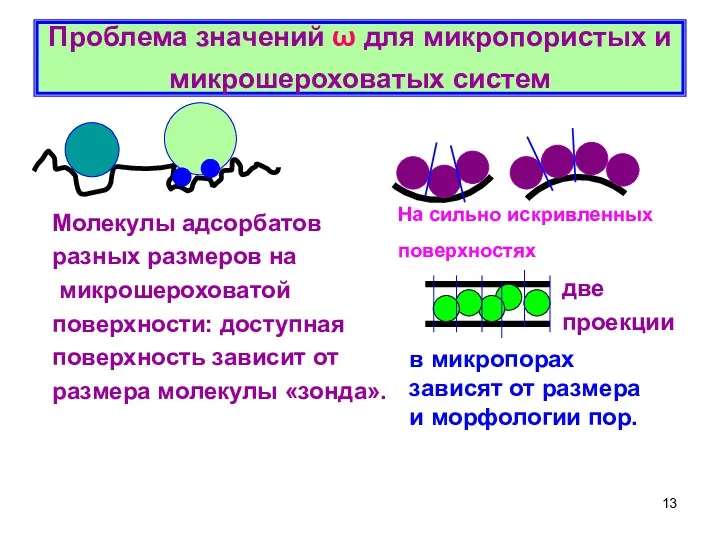
- 13. Проблема значений ω для микропористых и микрошероховатых систем
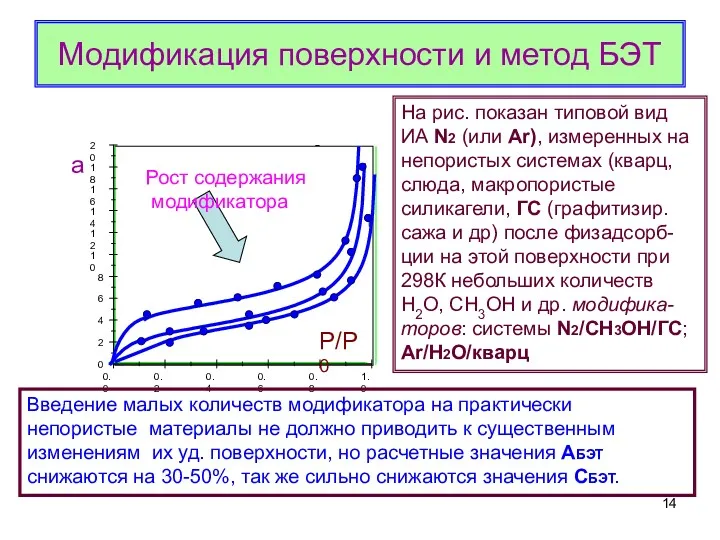
- 14. Модификация поверхности и метод БЭТ
- 15. Но как быть, если модифицирована только часть поверхности? Как обойтись без ω? Альтернатива – отказаться от
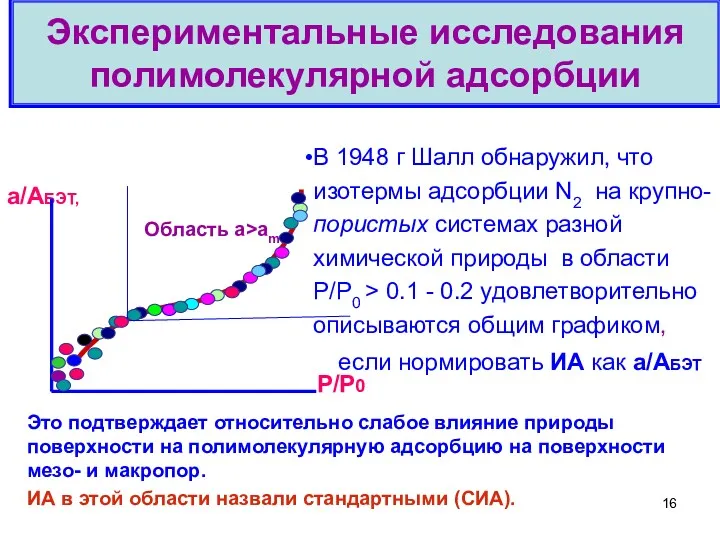
- 16. Экспериментальные исследования полимолекулярной адсорбции В 1948 г Шалл обнаружил, что изотермы адсорбции N2 на крупно- пористых
- 17. Идея СИА была подтверждена и развита многими авторами, получившими СИА для разных систем. Использовались разные способы
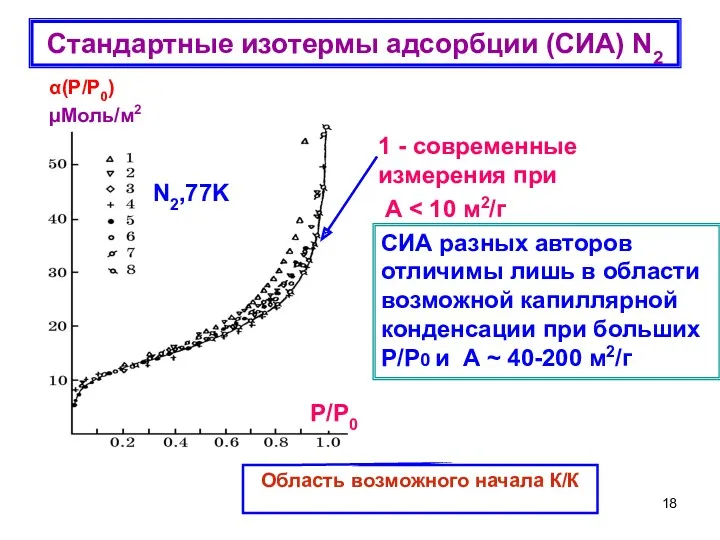
- 18. Стандартные изотермы адсорбции (СИА) N2 Область возможного начала К/К
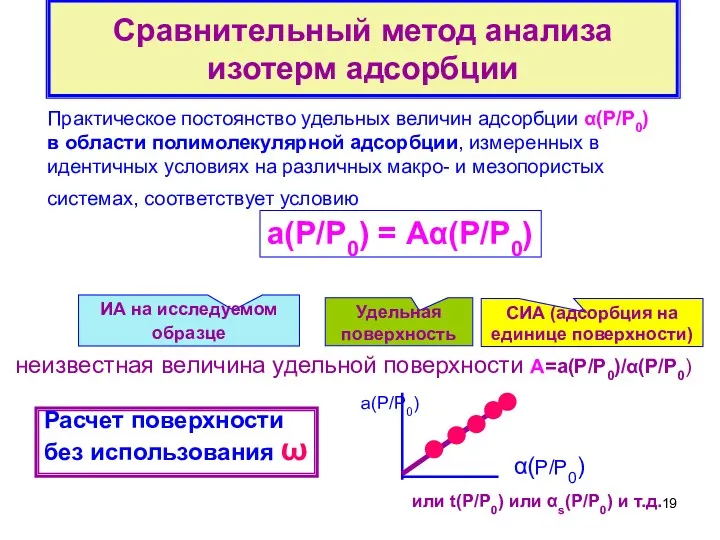
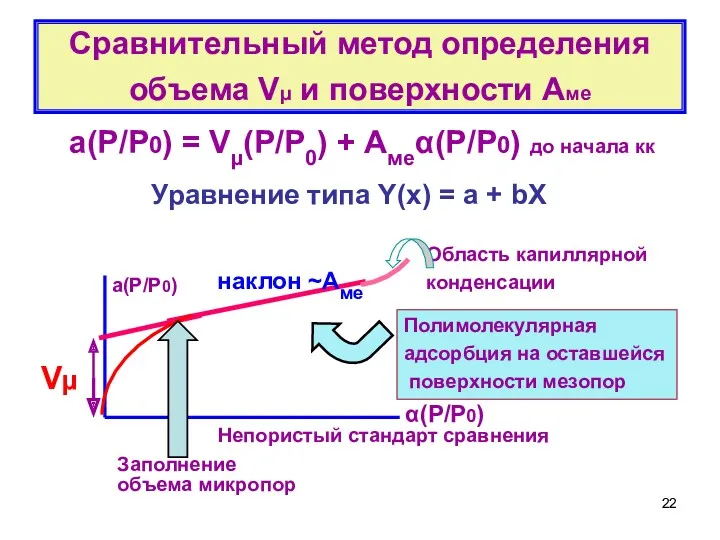
- 19. Сравнительный метод анализа изотерм адсорбции Практическое постоянство удельных величин адсорбции α(Р/Р0) в области полимолекулярной адсорбции, измеренных
- 20. Сравнительный метод анализа изотерм адсорбции Наличие микропор и капиллярной конденсации в мезопорах приводит к дополнительной адсорбции.
- 21. Сравнительный метод определения объема микропор Vµ и поверхности мезопор Aме ?
- 22. Сравнительный метод определения объема Vµ и поверхности Aме
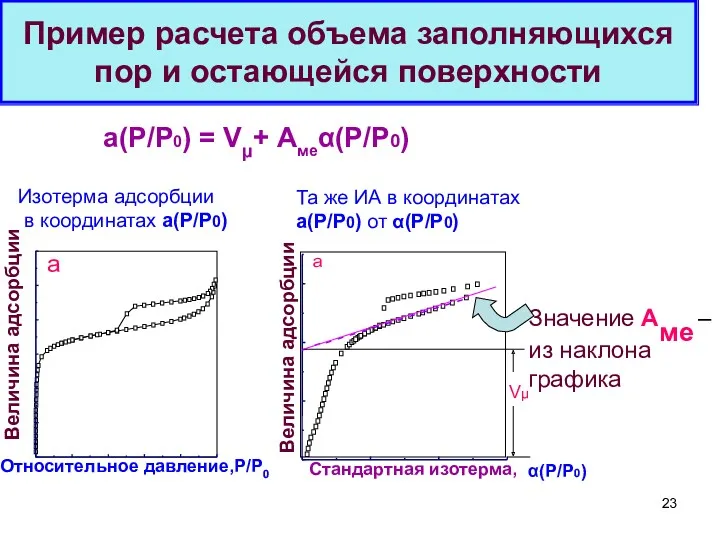
- 23. Пример расчета объема заполняющихся пор и остающейся поверхности
- 24. Сравнительный метод анализа изотерм адсорбции Такой сравнительный метод расчета А не- зависим от БЭТ, т.к. поверхность
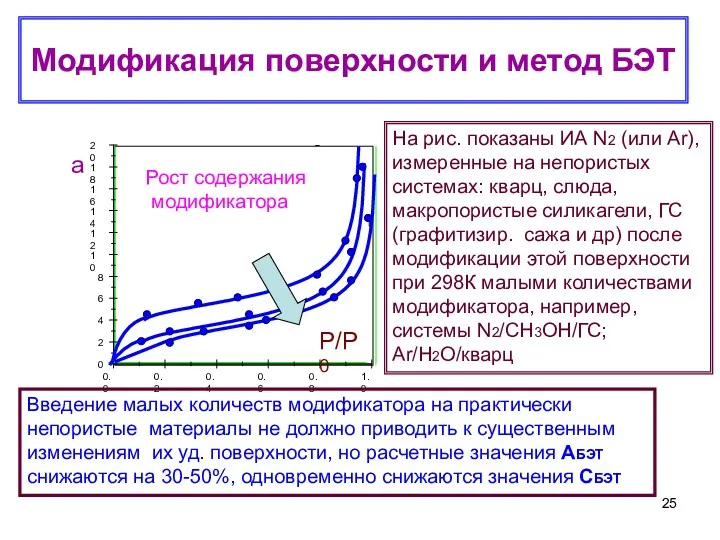
- 25. Модификация поверхности и метод БЭТ
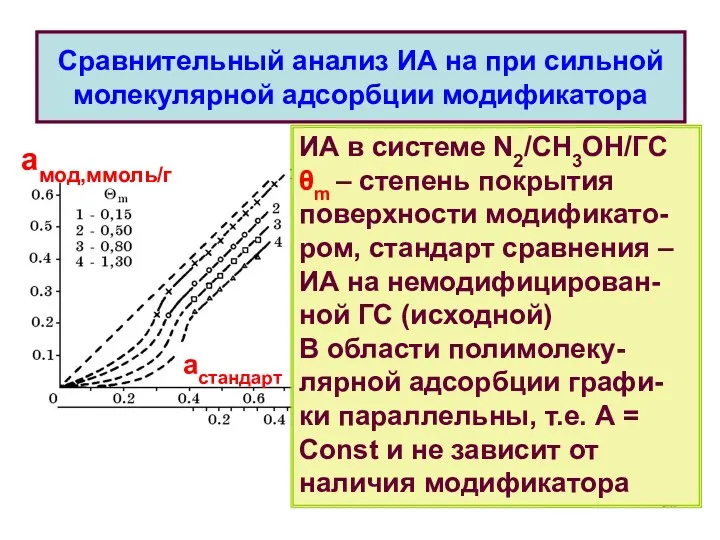
- 26. Сравнительный анализ ИА на при сильной молекулярной адсорбции модификатора астандарт амод,ммоль/г ИА в системе N2/СН3ОН/ГС θm
- 27. Сравнительные графики адсорбции N2 на микропористом TiO2, модифицированном нонаном (СН3(СН2)7СН3; данные Синга) Стандарт сравнения – СИА
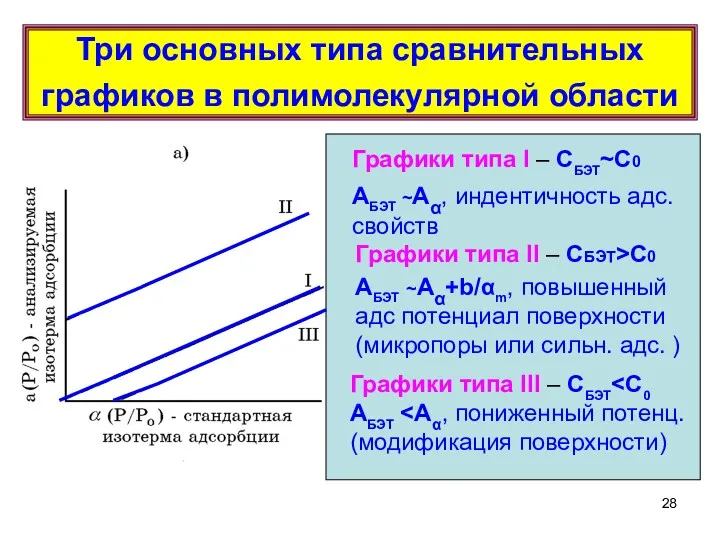
- 28. Три основных типа сравнительных графиков в полимолекулярной области
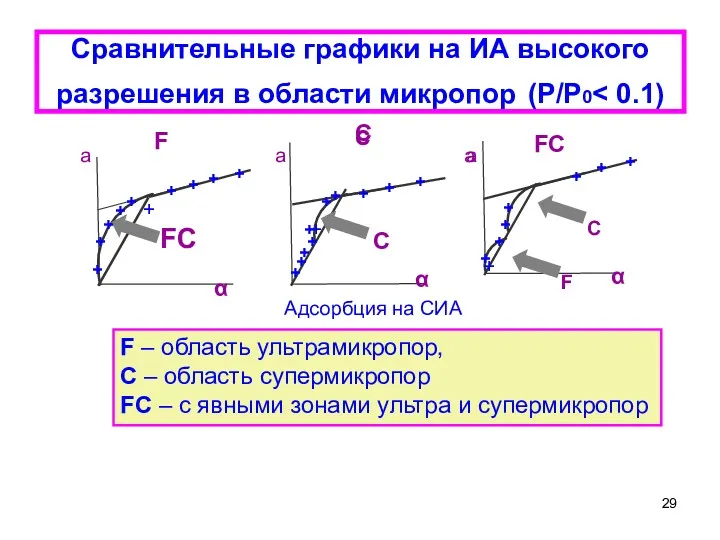
- 29. Сравнительные графики на ИА высокого разрешения в области микропор (Р/Р0
- 30. Проблема микропор Из других методов анализа микропористости кратко остановимся на некоторых возможностях Теории Объемного Заполнения Микропор
- 31. Основные постулаты ТОЗМ: - объемное заполнение микропор (вместо их послойного заполнения); адс. потенциал (дифференциальная мольная работа
- 32. Температурная инвариантность и ТОЗМ Важнейшее экспериментальное доказательство ТОЗМ – температурная инвариантность ИА – практическая независимость функции
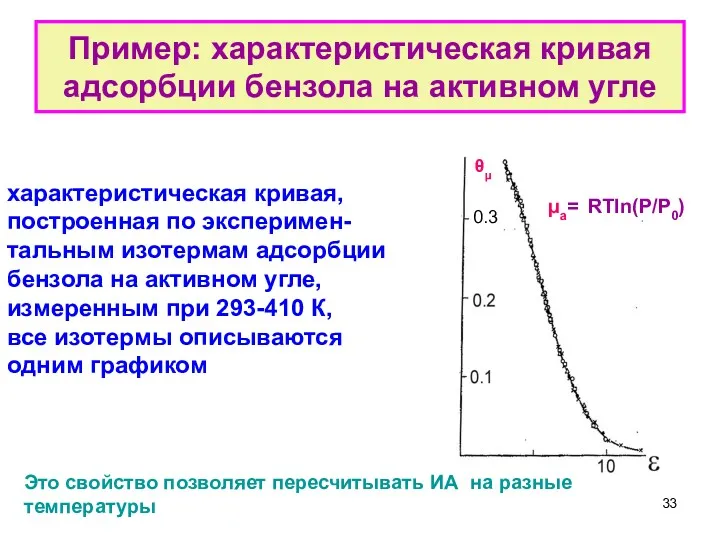
- 33. Пример: характеристическая кривая адсорбции бензола на активном угле
- 34. Уравнение Дубинина-Радушкевича (ДР) В простейшем случае характеристические кривые описываются уравнением Дубинина –Радушкевича, предложенным в 1947 г.
- 35. β - коэффициент афинности, численно равный отношению парахоров исследуе-мого и стандартного (N2 или C6H6) адсорбатов. Парахор
- 36. Адсорбция ряда газов при разных Т на активном угле в координатах уравнения ДР с учетом коэффициентов
- 37. Расчеты – по ДР lnW = ln(a/ρж) от [ln (/P/P0)]2 ИА в координатах ДР W/W0 =
- 39. Скачать презентацию
















![Расчеты – по ДР lnW = ln(a/ρж) от [ln (/P/P0)]2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/177699/slide-36.jpg)
 Биогенді (s.p.d) элементтермен олардың қосылыстарының медициналық және биологиялық маңызы
Биогенді (s.p.d) элементтермен олардың қосылыстарының медициналық және биологиялық маңызы Кислоты, их состав и названия
Кислоты, их состав и названия Карбоновые кислоты и их функциональные производные
Карбоновые кислоты и их функциональные производные Ароматические углеводороды
Ароматические углеводороды Гетерофазный катализ. (Лекция 20)
Гетерофазный катализ. (Лекция 20) Горение топлива
Горение топлива Використання радіоактивних ізотопів, як індикаторів у тваринництві і археології
Використання радіоактивних ізотопів, як індикаторів у тваринництві і археології Основные классы неорганических соединений
Основные классы неорганических соединений Соли, их классификация и свойства
Соли, их классификация и свойства Органічна хімія
Органічна хімія Розв’язування задач за рівняннями реакцій з використанням розчинів із певною масовою часткою розчиненої речовини. Урок 13-14
Розв’язування задач за рівняннями реакцій з використанням розчинів із певною масовою часткою розчиненої речовини. Урок 13-14 Жёсткость воды
Жёсткость воды Полисахариды: крахмал и целлюлоза
Полисахариды: крахмал и целлюлоза Растворы. Часть 2. Лекция №7
Растворы. Часть 2. Лекция №7 Химия атмосферы. Химические процессы в тропосфере
Химия атмосферы. Химические процессы в тропосфере Буферные системы
Буферные системы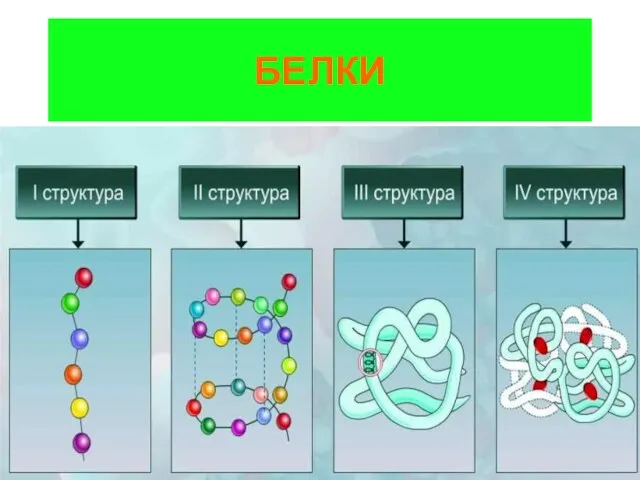 Белки. Строение
Белки. Строение Классификация химических элементов. Составитель. 8 класс
Классификация химических элементов. Составитель. 8 класс Минералы для ИЗБ
Минералы для ИЗБ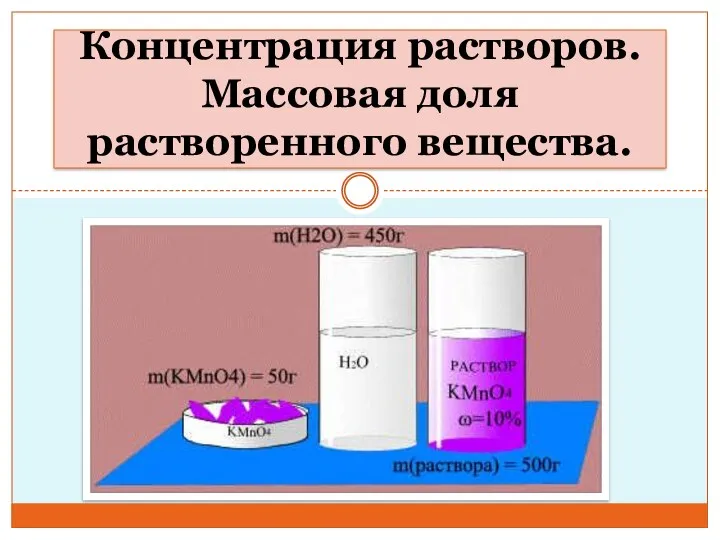 Концентрация растворов. Массовая доля растворенного вещества. Урок 1
Концентрация растворов. Массовая доля растворенного вещества. Урок 1 Химический элемент медь
Химический элемент медь Кинетика химических реакций
Кинетика химических реакций Кремний и его соединения
Кремний и его соединения Галогены. Расположите галогены в порядке их открытия
Галогены. Расположите галогены в порядке их открытия Важнейшие реакции в органической химии
Важнейшие реакции в органической химии Технология производства аминоальдегидных смол
Технология производства аминоальдегидных смол Углерод. Физические и химические свойства
Углерод. Физические и химические свойства Гидролиз солей
Гидролиз солей