Кристаллофизика_часть_1 презентация

ГЕОМЕТРИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
Для направлений:
«Техническая физика»,
«Электроника и наноэлектроника»,
«Материаловедение и технология материалов»
«Электроника и микроэлектроника»
(IV – семестр)
В.В. Гераськин

ПРИОБРЕТАЕМЫЕ КОМПЕТЕНЦИИ
Готовность:
- использовать кристаллографическую символику при описании симметрии кристаллов и кристаллических структур;
- использовать построения стереографических проекций элементов симметрии и граней кристаллов с применением различных кристаллографических сеток для описания симметрии кристаллических многогранников;
- использовать стереографические построения для решения кристаллографических задач;
- описывать симметрию кристаллических многогранников структур по международным стандартам;
- описывать симметрию кристаллических многогранников по международным стандартам.

Научить использовать теорию симметрии и метод кристаллографических проекций для описания и анализа структуры кристаллов.
Разделы курса:
1. симметрия кристаллических многогранников;
2. симметрия кристаллических структур;
3. элементы кристаллохимии и дефекты в кристаллах.
Цель обучения

Раздел 1
Симметрия кристаллических многогранников
Лекция 1
Структура кристалла и понятие о пространственной решетке
У кристаллов закономерное внутреннее атомарное строение,
это приводит к тому, что атомная структура кристаллов обладает трансляционно упорядоченным строением
Расположение отдельных Укладка
группировок атомов крупных
в кристаллической структуре молекул
Другим важнейшим свойством кристаллов является однородность
Третья характеристика кристаллов - анизотропия физических свойств
Кристалл - это одна из форм конденсированного состояния вещества
Идеальный кристалл - однородная анизотропная
симметричная конденсированная среда,
обладающая трансляционно упорядоченным атомным строением и способная самоограняться в процессе роста

Закон постоянства углов
Углы между соответственными гранями (и ребрами)
во всех кристаллах одного вещества одной полиморфной
модификации при одинаковых условиях постоянны
Кристаллы кварца Различные формы кристаллов кварца
Сечения кристаллов кварца перпендикулярные ребру ab

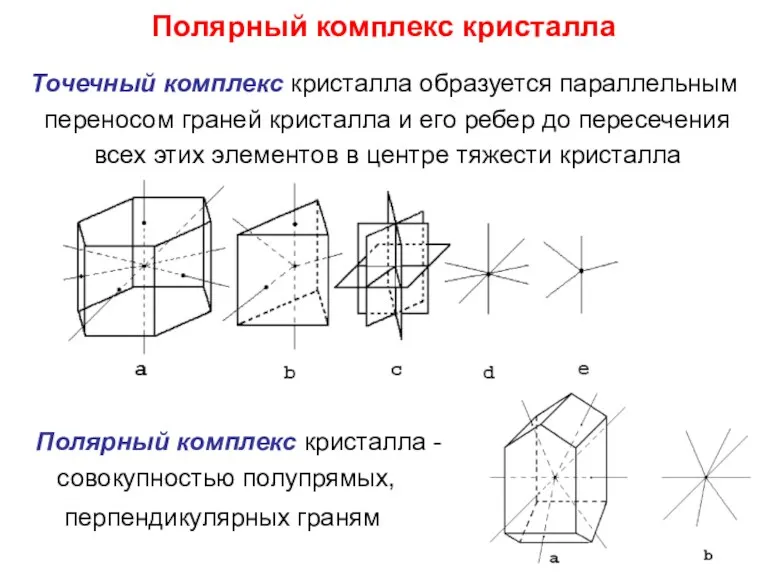
Полярный комплекс кристалла
Точечный комплекс кристалла образуется параллельным
переносом граней кристалла и его ребер до пересечения
всех этих элементов в центре тяжести кристалла
Полярный комплекс кристалла -
совокупностью полупрямых,
перпендикулярных граням

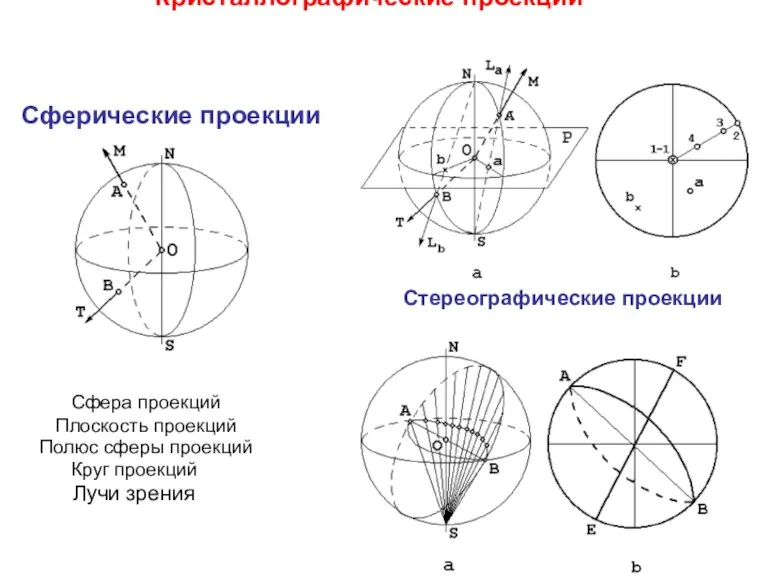
Кристаллографические проекции
Сферические проекции
Стереографические проекции
Сфера проекций
Плоскость проекций
Полюс сферы проекций Круг проекций
Лучи зрения

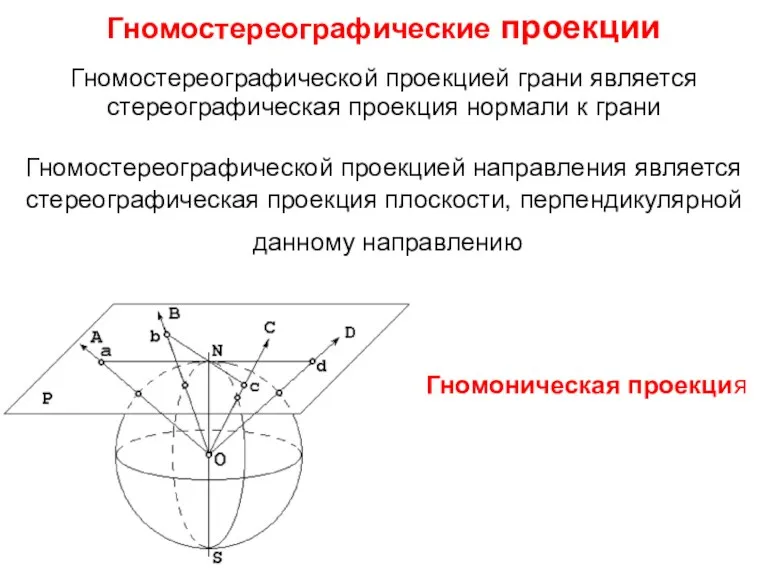
Гномостереографические проекции
Гномостереографической проекцией грани является
стереографическая проекция нормали к грани
Гномостереографической проекцией направления является
стереографическая проекция плоскости, перпендикулярной
данному направлению
Гномоническая проекция

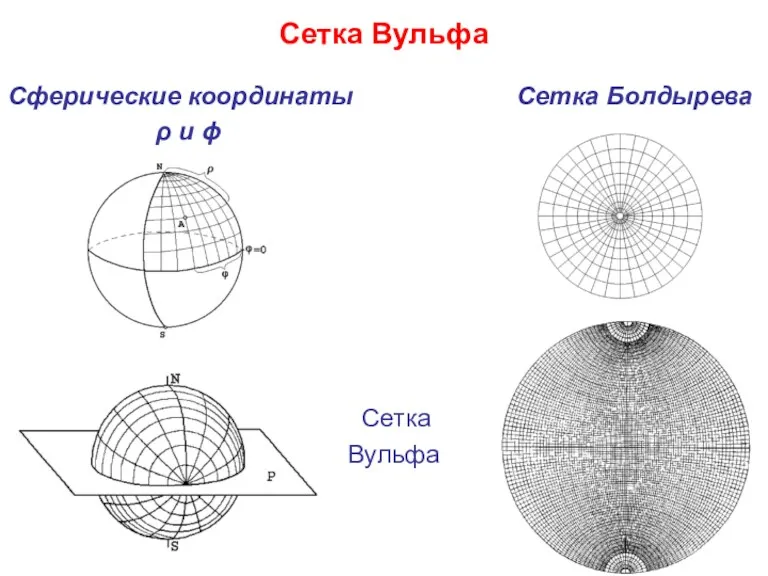
Сетка Вульфа
Сферические координаты Сетка Болдырева
ρ и ϕ
Сетка
Вульфа

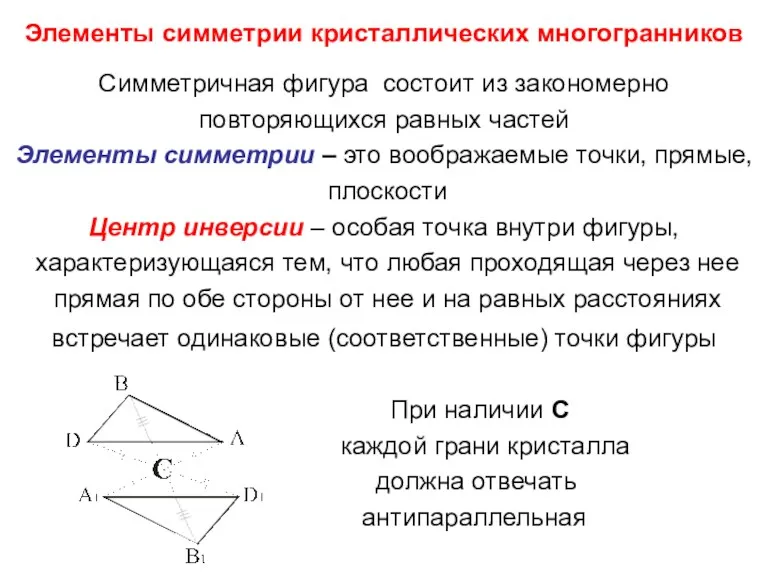
Элементы симметрии кристаллических многогранников
Симметричная фигура состоит из закономерно
повторяющихся равных частей
Элементы симметрии – это воображаемые точки, прямые,
плоскости
Центр инверсии – особая точка внутри фигуры,
характеризующаяся тем, что любая проходящая через нее
прямая по обе стороны от нее и на равных расстояниях
встречает одинаковые (соответственные) точки фигуры
При наличии С
каждой грани кристалла
должна отвечать
антипараллельная

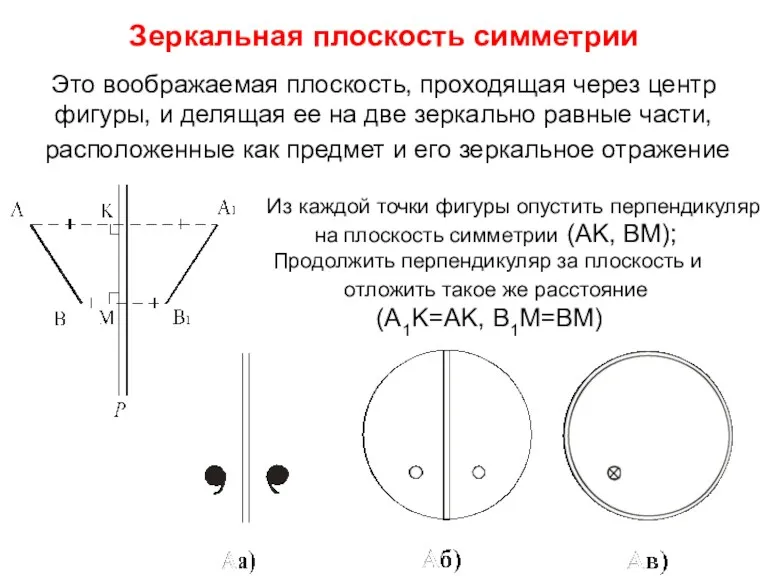
Зеркальная плоскость симметрии
Это воображаемая плоскость, проходящая через центр
фигуры, и делящая ее на две зеркально равные части,
расположенные как предмет и его зеркальное отражение
Из каждой точки фигуры опустить перпендикуляр
на плоскость симметрии (AK, BM);
Продолжить перпендикуляр за плоскость и
отложить такое же расстояние
(A1K=AK, B1M=BM)

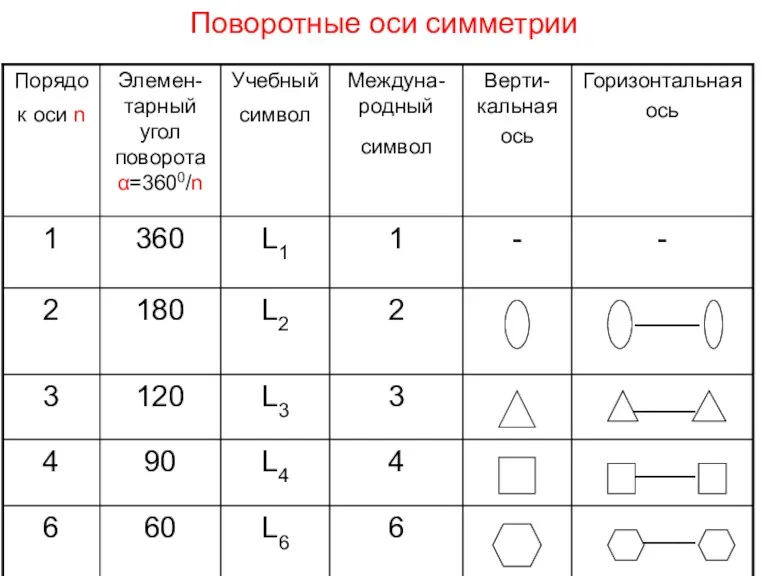
Поворотные оси симметрии
Поворотная ось симметрии – воображаемая прямая
линия, проходящая через центр фигуры, вокруг которой
несколько раз повторяются одинаковые части фигуры
Порядок оси симметрии (n) - число равных частей фигуры,
повторяющихся вокруг нее
Элементарный угол поворота (α) - минимальный угол,
приводящий фигуру к самосовмещению
Строение кристаллов делает
невозможным существование
в них осей симметрии
пятого порядка и
порядка выше шестого

Поворотные оси симметрии

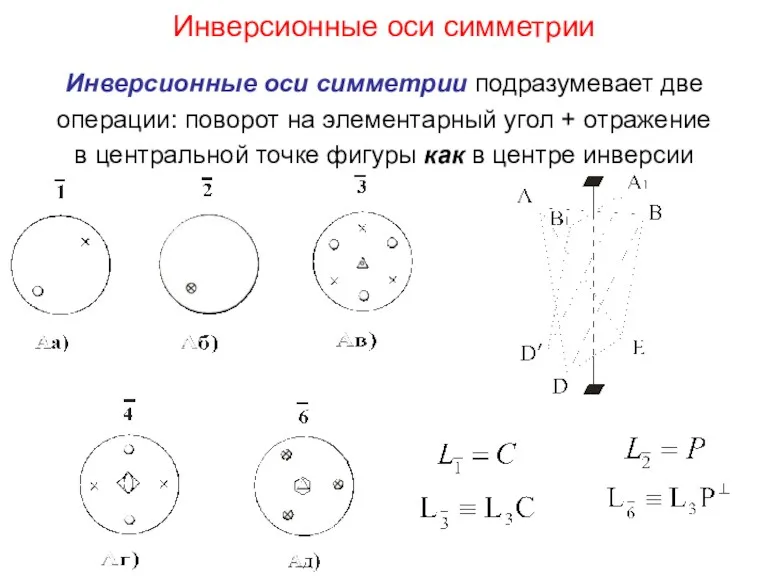
Инверсионные оси симметрии
Инверсионные оси симметрии подразумевает две
операции: поворот на элементарный угол + отражение
в центральной точке фигуры как в центре инверсии

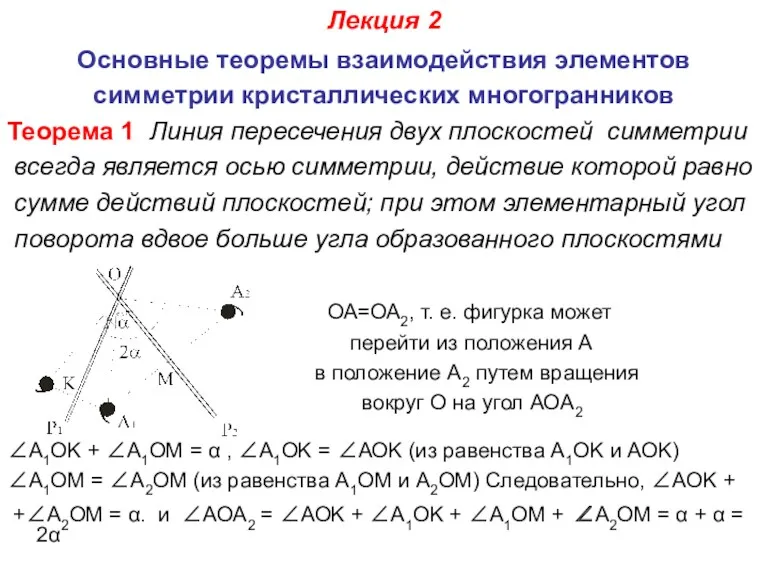
Лекция 2
Основные теоремы взаимодействия элементов
симметрии кристаллических многогранников
Теорема 1 Линия пересечения двух плоскостей симметрии
всегда является осью симметрии, действие которой равно
сумме действий плоскостей; при этом элементарный угол
поворота вдвое больше угла образованного плоскостями
ОА=ОА2, т. е. фигурка может
перейти из положения А
в положение А2 путем вращения
вокруг О на угол АОА2
∠А1ОK + ∠А1ОM = α , ∠А1ОK = ∠АОK (из равенства А1ОK и АОK)
∠А1ОМ = ∠А2ОМ (из равенства А1ОМ и А2ОМ) Следовательно, ∠АОK +
+∠А2ОM = α. и ∠АОА2 = ∠АОK + ∠А1ОK + ∠А1ОM + ∠А2ОМ = α + α = 2α

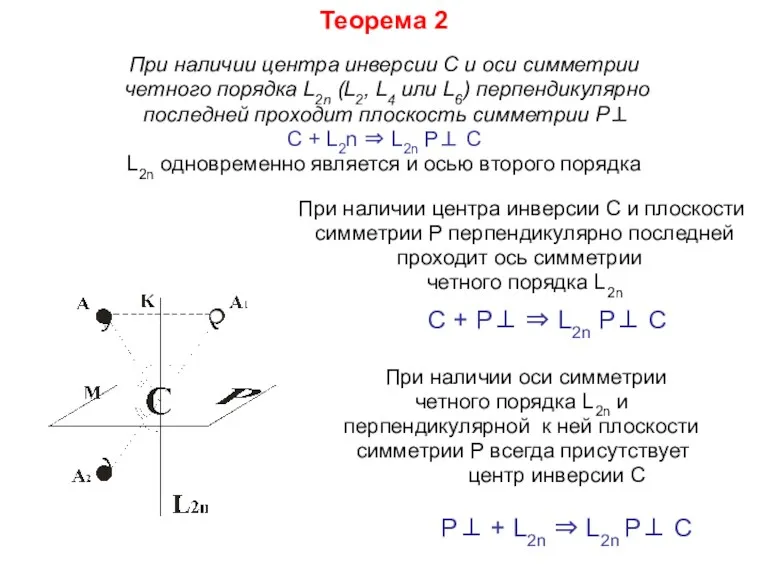
Теорема 2
При наличии центра инверсии С и оси симметрии
четного порядка L2n (L2, L4 или L6) перпендикулярно
последней проходит плоскость симметрии Р⊥
С + L2n ⇒ L2n Р⊥ С
L2n одновременно является и осью второго порядка
При наличии центра инверсии С и плоскости
симметрии P перпендикулярно последней
проходит ось симметрии
четного порядка L2n
С + Р⊥ ⇒ L2n Р⊥ С
При наличии оси симметрии
четного порядка L2n и
перпендикулярной к ней плоскости
симметрии P всегда присутствует
центр инверсии С
Р⊥ + L2n ⇒ L2n Р⊥ С

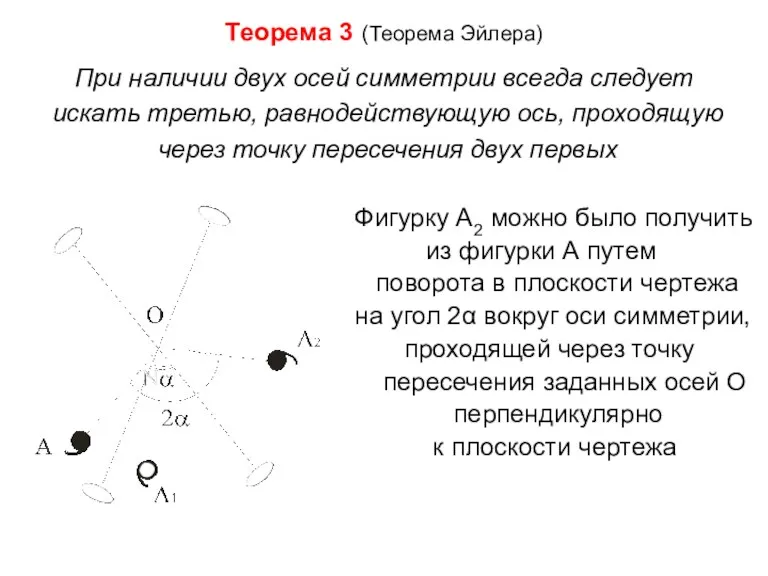
Теорема 3 (Теорема Эйлера)
При наличии двух осей симметрии всегда следует
искать третью, равнодействующую ось, проходящую
через точку пересечения двух первых
Фигурку А2 можно было получить
из фигурки А путем
поворота в плоскости чертежа
на угол 2α вокруг оси симметрии,
проходящей через точку
пересечения заданных осей О
перпендикулярно
к плоскости чертежа

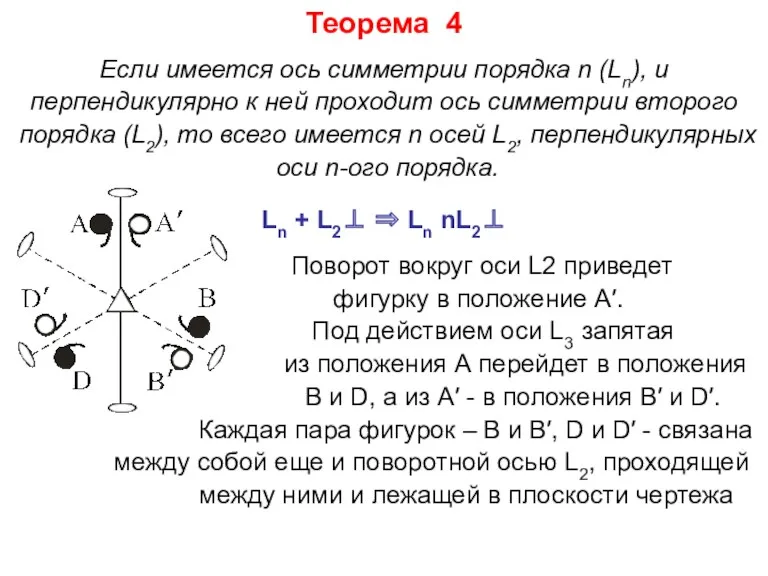
Теорема 4
Если имеется ось симметрии порядка n (Ln), и
перпендикулярно к ней проходит ось симметрии второго
порядка (L2), то всего имеется n осей L2, перпендикулярных
оси n-ого порядка.
Ln + L2⊥ ⇒ Ln nL2⊥
Поворот вокруг оси L2 приведет
фигурку в положение А′.
Под действием оси L3 запятая
из положения А перейдет в положения
В и D, а из А′ - в положения В′ и D′.
Каждая пара фигурок – В и В′, D и D′ - связана
между собой еще и поворотной осью L2, проходящей
между ними и лежащей в плоскости чертежа

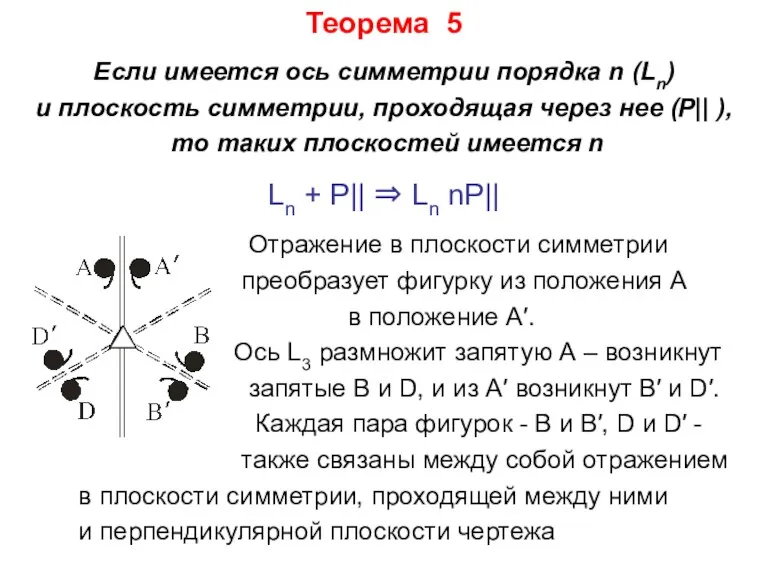
Теорема 5
Если имеется ось симметрии порядка n (Ln)
и плоскость симметрии, проходящая через нее (P|| ),
то таких плоскостей имеется n
Ln + P|| ⇒ Ln nP||
Отражение в плоскости симметрии
преобразует фигурку из положения А
в положение А′.
Ось L3 размножит запятую А – возникнут
запятые В и D, и из А′ возникнут В′ и D′.
Каждая пара фигурок - В и В′, D и D′ -
также связаны между собой отражением
в плоскости симметрии, проходящей между ними
и перпендикулярной плоскости чертежа

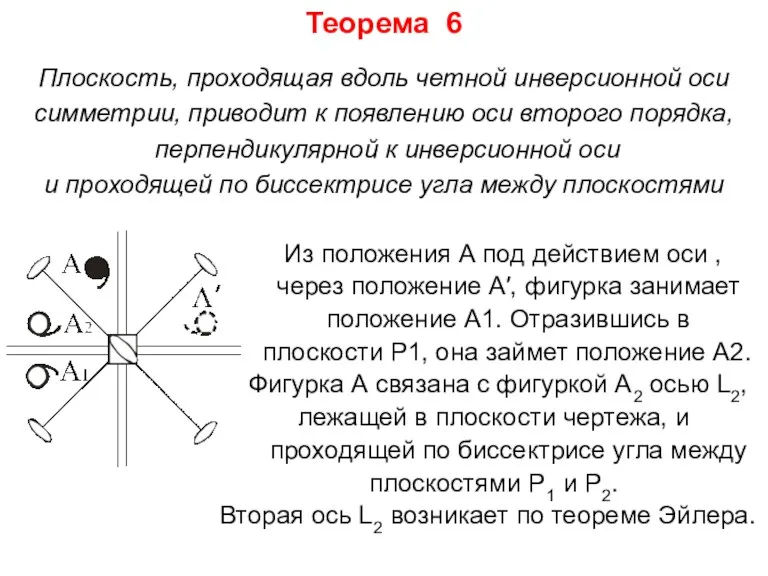
Теорема 6
Плоскость, проходящая вдоль четной инверсионной оси
симметрии, приводит к появлению оси второго порядка,
перпендикулярной к инверсионной оси
и проходящей по биссектрисе угла между плоскостями
Из положения А под действием оси ,
через положение А′, фигурка занимает
положение А1. Отразившись в
плоскости Р1, она займет положение А2.
Фигурка А связана с фигуркой А2 осью L2,
лежащей в плоскости чертежа, и
проходящей по биссектрисе угла между
плоскостями P1 и P2.
Вторая ось L2 возникает по теореме Эйлера.

Единичные и полярные направления
Не повторяющееся в кристалле направление называется единичным
Полярное направление – такое направление,
концы которого нельзя совместить действием элементов
симметрии, присущих данному кристаллу
полярными не могут быть направления:
в присутствии центра инверсии;
перпендикулярные плоскости симметрии;
перпендикулярные оси второго порядка

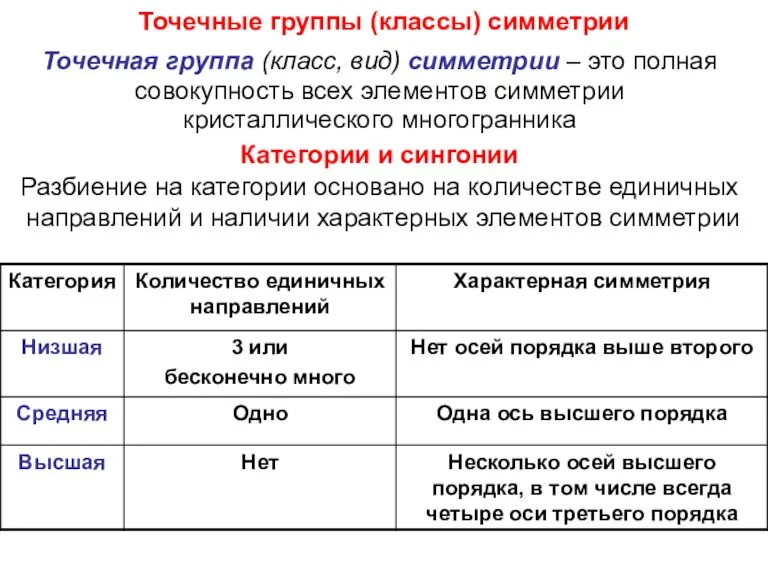
Точечные группы (классы) симметрии
Точечная группа (класс, вид) симметрии – это полная
совокупность всех элементов симметрии
кристаллического многогранника
Категории и сингонии
Разбиение на категории основано на количестве единичных
направлений и наличии характерных элементов симметрии

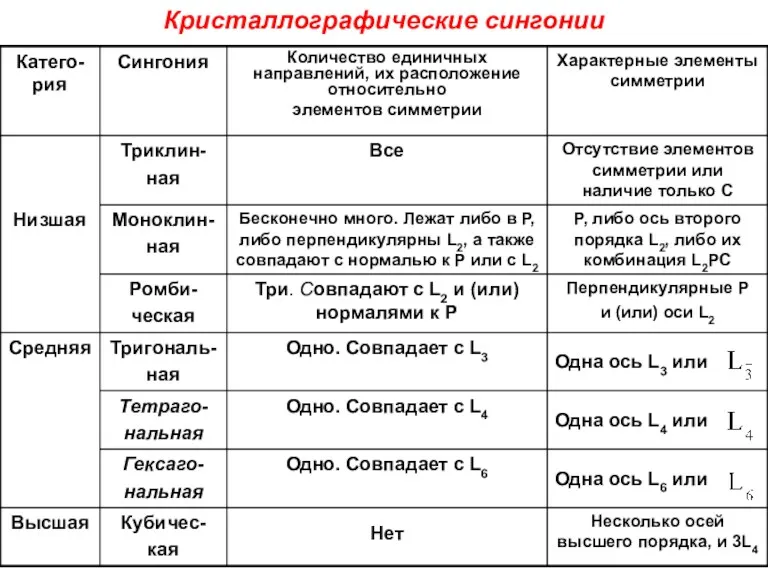
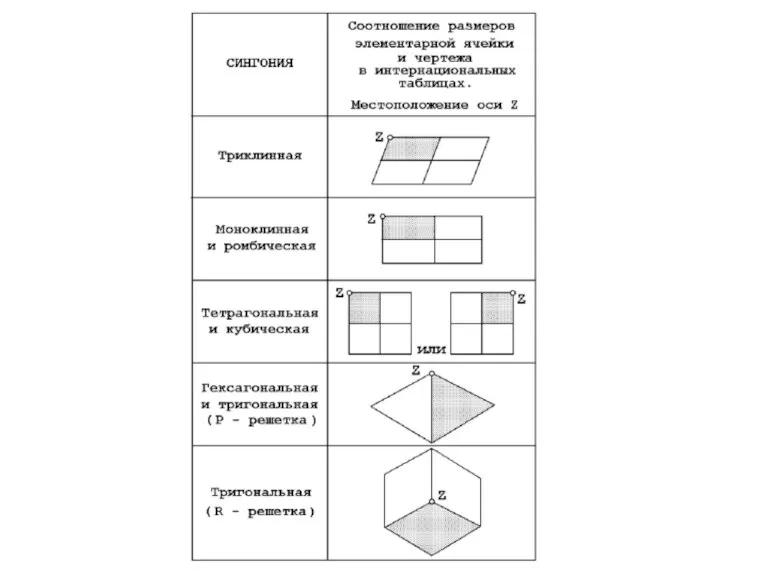
Кристаллографические сингонии

Принцип вывода 32 классов симметрии
Формула симметрии - это записанные все элементы симметрии кристалла: сначала оси симметрии (Ln), затем плоскости (P), и центр (C), например: 3L44L36L29PС
Для сингонии берут исходный характерный элемент данной симметрии (L1, L2, L3, L4, L6, 3L24L3 и инверсионные оси 3, 4 и 6 порядка) и добавляют возможные элементы симметрии
Тетрагональная сингония:
L4 – примитивный класс;
L4 + С → L4РС – центральный класс (L4 + ┴Р → L4РС );
L4 + L2 → L44L2 – аксиальный класс;
L4 + //Р→ L44Р – планальный класс;
L4 + //Р + С → L4 4L25РС - планаксиальный класс;
(L4 + L2 + //Р → L4 4L25РС , L4 + L2 + С → L4 4L25РС , L4 + ┴Р + //Р → L4 4L25РС)
- инверсионно-приметивный класс;
+ //Р→ 2L2 4Р - инверсионно-планальный класс

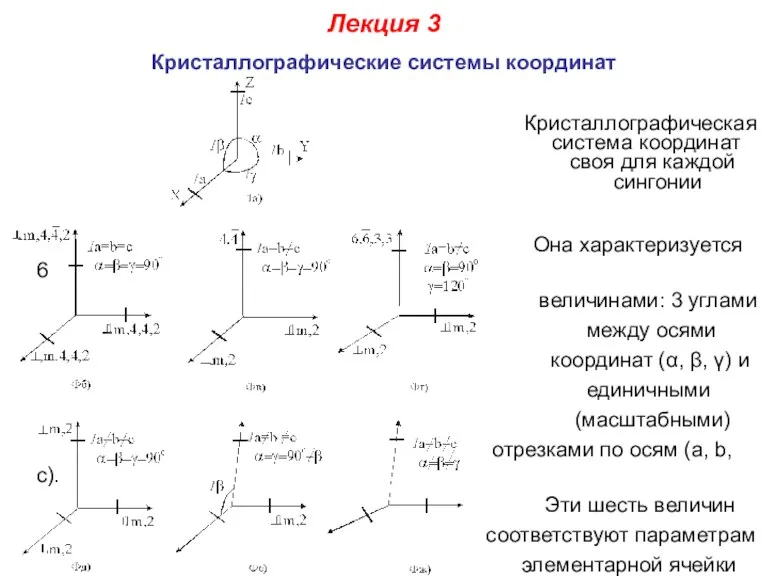
Лекция 3
Кристаллографические системы координат
Кристаллографическая
система координат
своя для каждой
сингонии Она характеризуется 6
величинами: 3 углами
между осями
координат (α, β, γ) и
единичными
(масштабными)
отрезками по осям (a, b, c).
Эти шесть величин
соответствуют параметрам
элементарной ячейки
кристалла

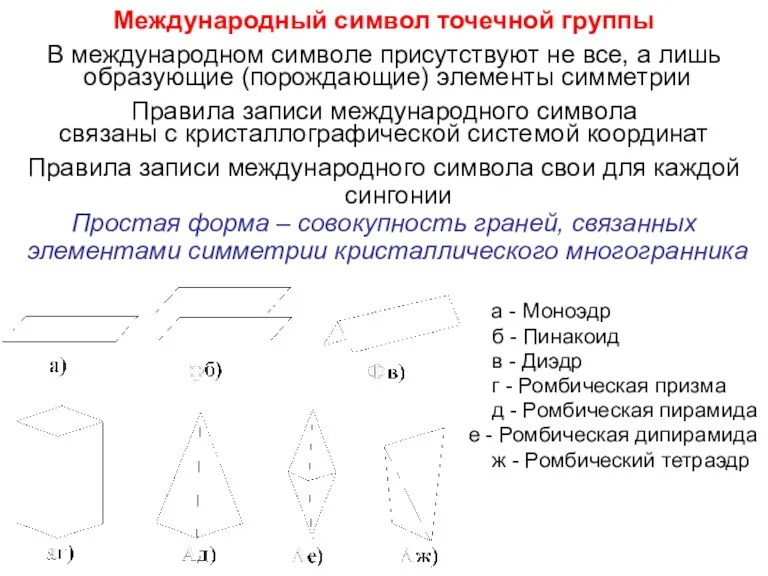
Международный символ точечной группы
В международном символе присутствуют не все, а лишь
образующие (порождающие) элементы симметрии
Правила записи международного символа
связаны с кристаллографической системой координат
Правила записи международного символа свои для каждой сингонии
Простая форма – совокупность граней, связанных
элементами симметрии кристаллического многогранника
а - Моноэдр
б - Пинакоид
в - Диэдр
г - Ромбическая призма
д - Ромбическая пирамида
е - Ромбическая дипирамида
ж - Ромбический тетраэдр

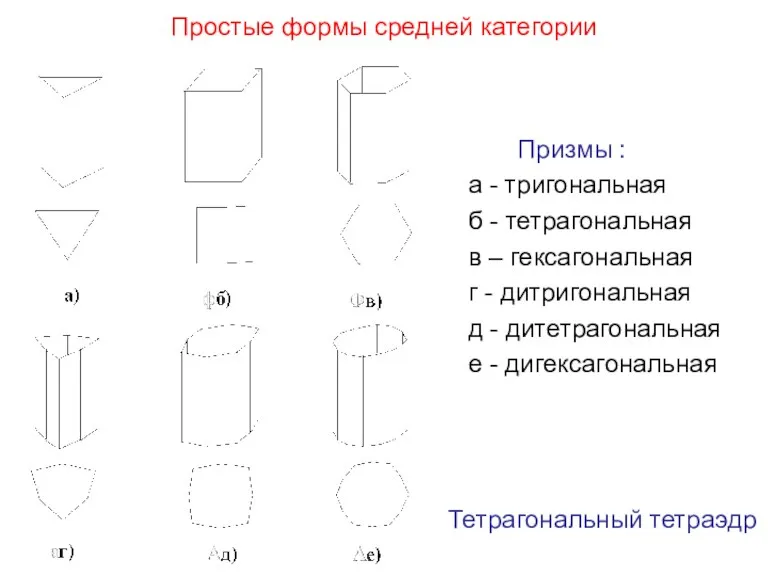
Простые формы средней категории
Призмы :
а - тригональная
б - тетрагональная
в – гексагональная
г - дитригональная
д - дитетрагональная
е - дигексагональная
Тетрагональный тетраэдр

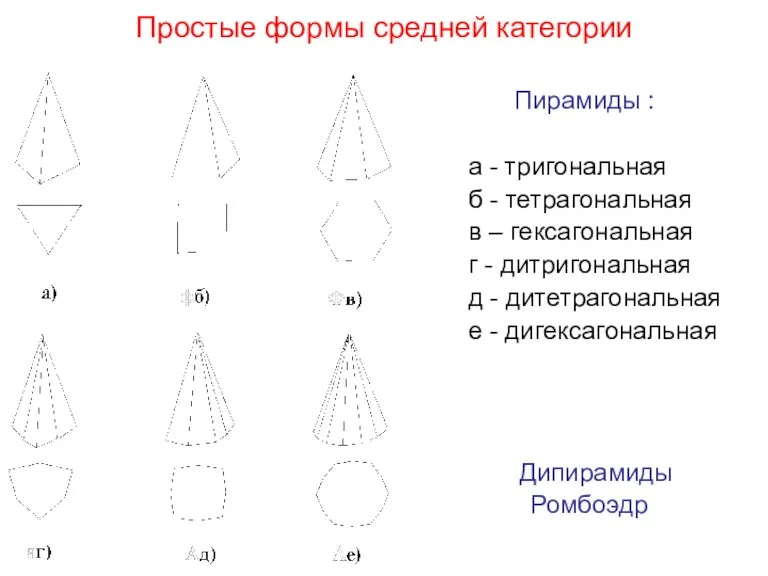
Простые формы средней категории
Пирамиды :
а - тригональная
б - тетрагональная
в – гексагональная
г - дитригональная
д - дитетрагональная
е - дигексагональная
Дипирамиды
Ромбоэдр

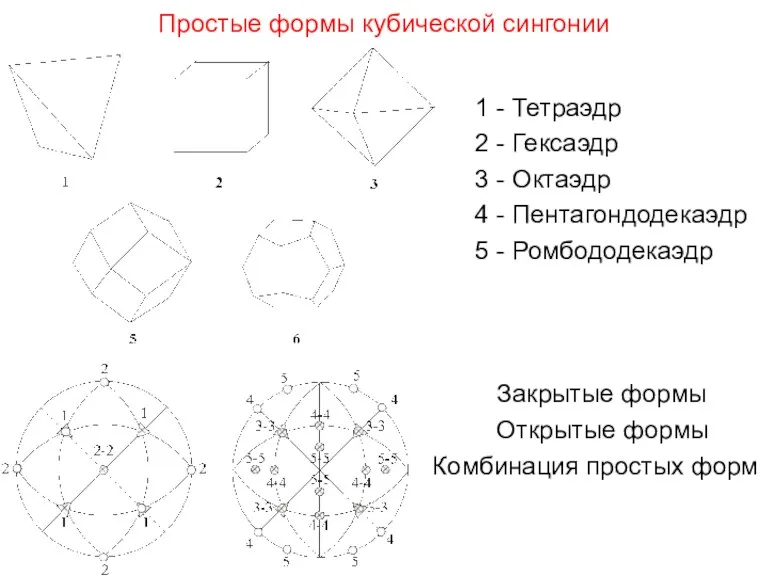
Простые формы кубической сингонии
1 - Тетраэдр
2 - Гексаэдр
3 - Октаэдр 4 - Пентагондодекаэдр
5 - Ромбододекаэдр
Закрытые формы
Открытые формы
Комбинация простых форм

Индицирование кристаллов
Индицирование узлов
Символ узла - [[mnp]] – совокупность чисел m, n, p,
заключенных в двойные квадратные скобки
Индицирование направлений (ребер кристалла)
Если направление проходит через начало координат [[000]],
то символом направления являются координаты [[mnp]]
любой точки через которую проходит это направление,
приведенные к взаимно простым целым числам [mnp]

Индицирование плоскостей (граней кристалла)
Закон рациональности отношений параметров
Двойные отношения параметров, отсекаемых двумя
любыми гранями кристалла на трех пересекающихся
ребрах его, равны отношениям целых и сравнительно
малых чисел
Если узлы плоских сеток (граней) А1В1С1 и
А2В2С2 лежат на самих ребрах 0I, OII и 0III,
то параметры граней соответственно равны:
r1a, s1b и t1c для грани А1В1С1 и r2a, s2b и
t2c для грани А2В2С2, где ri, si и ti – целые
числа ( r1 = 2, s1 = 3, t1 = 1, r2 = 8, s2 = 6, t2 = 3)
Двойные отношения параметров равны:
так как ri, si и ti целые числа, то

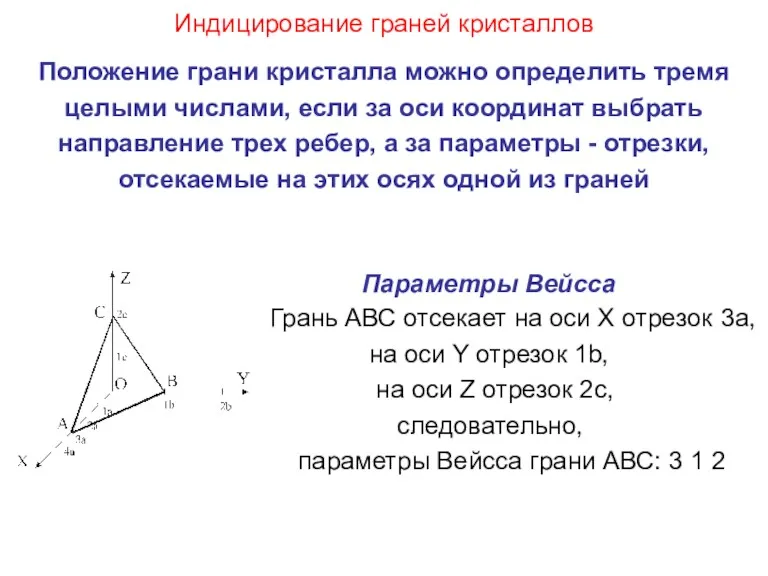
Индицирование граней кристаллов
Положение грани кристалла можно определить тремя
целыми числами, если за оси координат выбрать
направление трех ребер, а за параметры - отрезки,
отсекаемые на этих осях одной из граней
Параметры Вейсса
Грань АВС отсекает на оси X отрезок 3а,
на оси Y отрезок 1b,
на оси Z отрезок 2с,
следовательно,
параметры Вейсса грани АВС: 3 1 2

Индексы Миллера
это величины, обратно пропорциональные отрезкам (в осевых
единицах а, b, с), которые грань отсекает на трех
координатных осях, приведенные к взаимно простым
целым числам и заключенные в круглые скобки – (hkl)
Индексы Миллера являются величинами обратными параметрам Вейсса и приведены к целым числам:
Единичная грань – грань, отсекающая единичные отрезки на всех трех координатных осях - (111)
Грани, принадлежащие одной простой форме, образуют
совокупность симметрично-эквивалентных плоскостей {hkl}
и имеют одинаковый набор индексов Миллера в символе

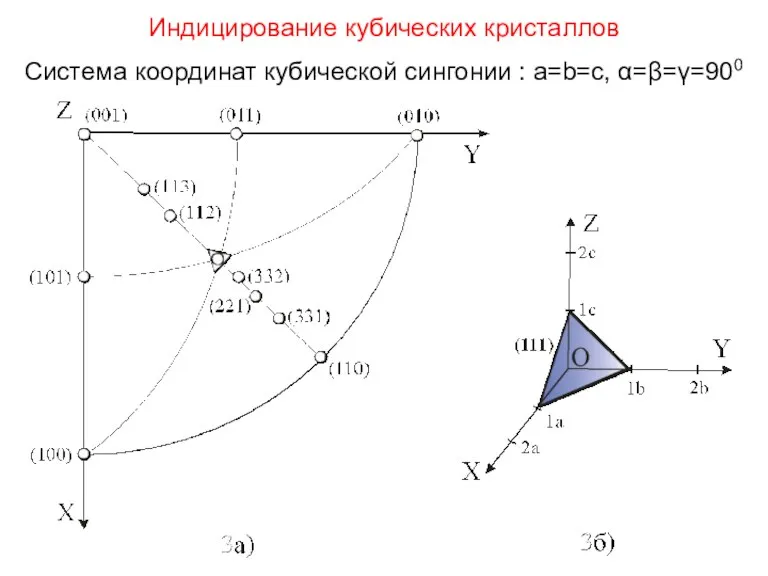
Индицирование кубических кристаллов
Система координат кубической сингонии : a=b=c, α=β=γ=900

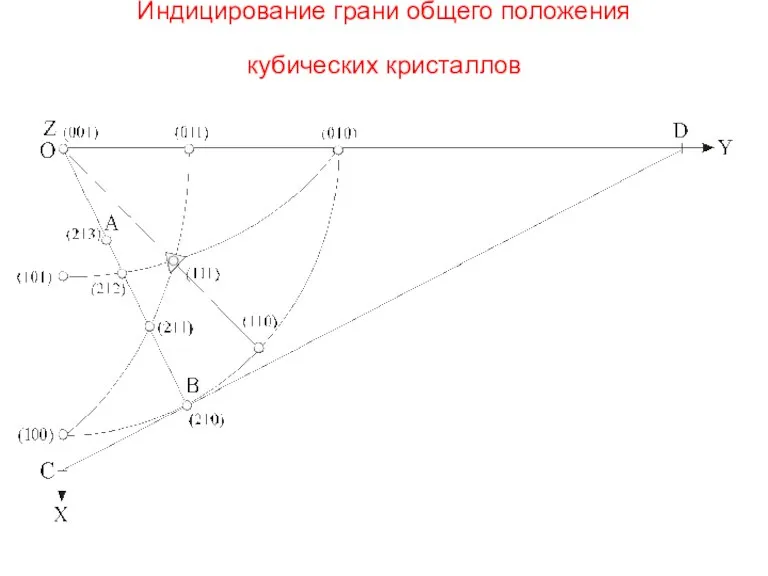
Индицирование грани общего положения
кубических кристаллов

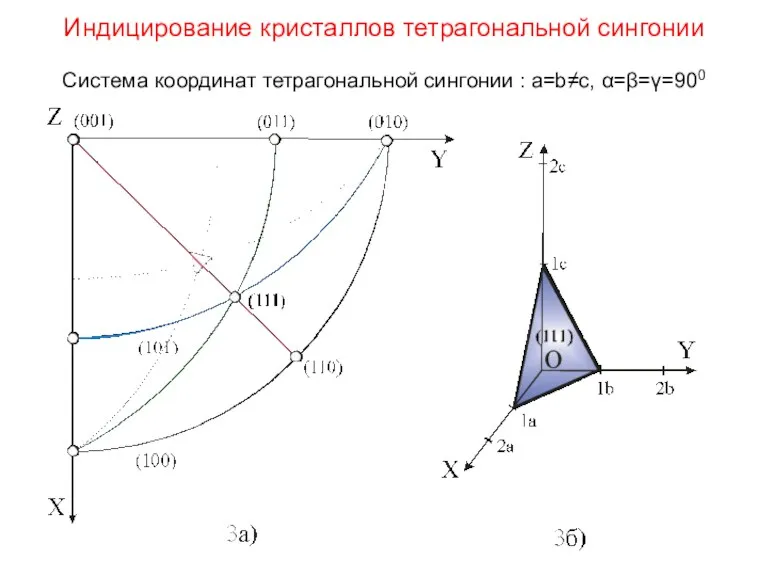
Индицирование кристаллов тетрагональной сингонии
Система координат тетрагональной сингонии : a=b≠c, α=β=γ=900

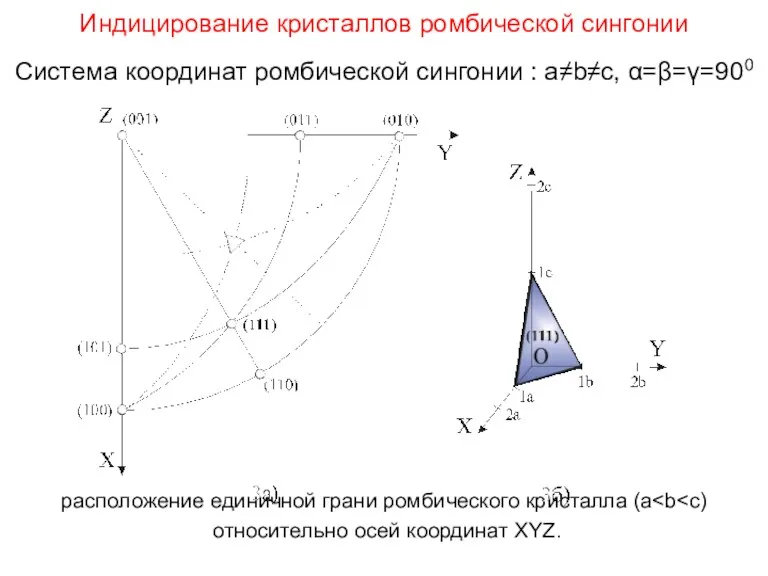
Индицирование кристаллов ромбической сингонии
Система координат ромбической сингонии : a≠b≠c, α=β=γ=900
расположение единичной грани ромбического кристалла (a
относительно осей координат XYZ.

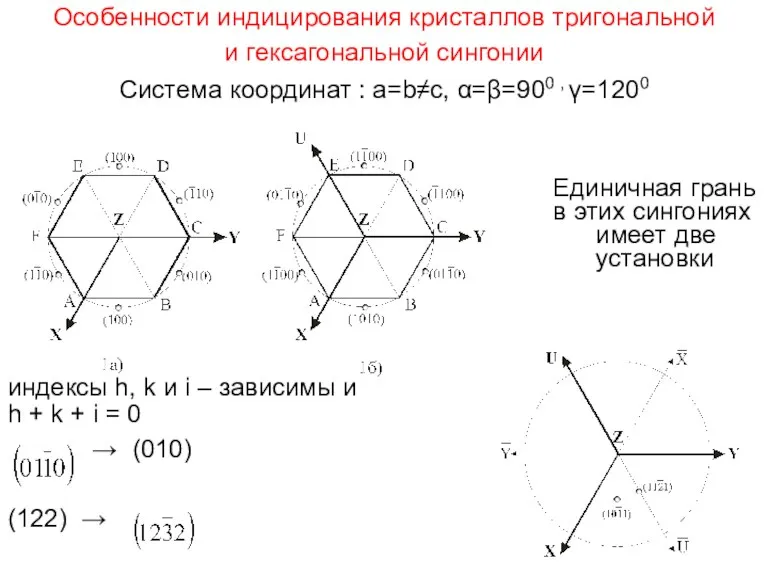
Особенности индицирования кристаллов тригональной
и гексагональной сингонии
Система координат : a=b≠c, α=β=900 , γ=1200
Единичная грань
в этих сингониях
имеет две
установки
индексы h, k и i – зависимы и
h + k + i = 0
→ (010)
(122) →

Определение символа грани кристалла по методу косинусов
Для ортогональной системы координат
Из треугольников AON, BON и CON
Кубическая сингония
Тетрагональная сингония
Гексагональная сингония

Зоны в кристаллах
Зона (пояс) в кристалле – совокупность граней,
пересекающихся по параллельным ребрам.
Ось зоны – общее направление этих ребер.
Критерий принадлежности грани (hkl) к зоне с осью [uvw]:
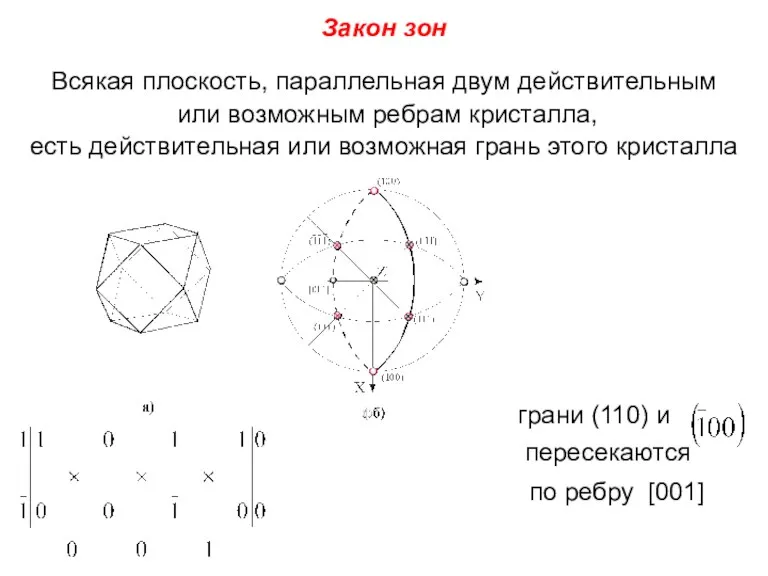
Символ ребра [mnp], пересекающихся граней (h1k1l1) и (h2k2l2)

Закон зон
Всякая плоскость, параллельная двум действительным
или возможным ребрам кристалла,
есть действительная или возможная грань этого кристалла
грани (110) и
пересекаются
по ребру [001]

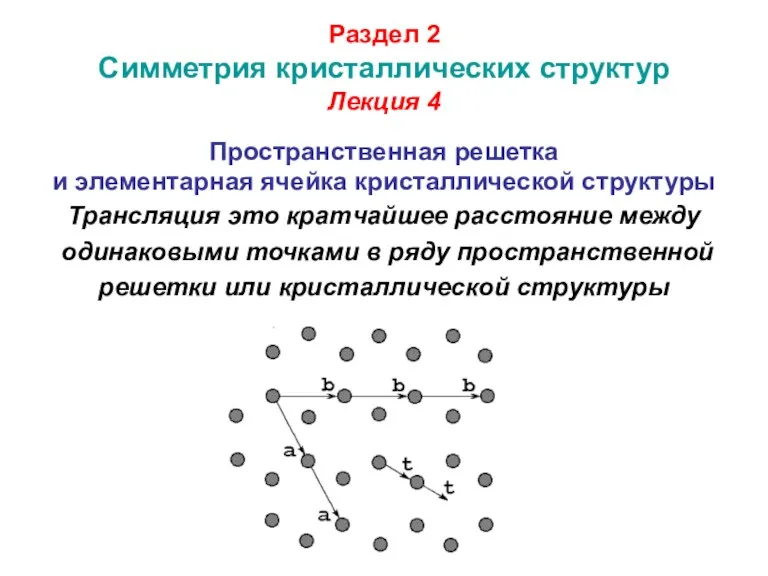
Раздел 2
Симметрия кристаллических структур
Лекция 4
Пространственная решетка
и элементарная ячейка кристаллической структуры
Трансляция это кратчайшее расстояние между
одинаковыми точками в ряду пространственной
решетки или кристаллической структуры

Пространственная решетка это тройка элементарных некомпланарных трансляций или система эквивалентных узлов, преобразующихся друг в друга с помощью трех основных трансляций, или же система одинаковых параллелепипедов, совмещающихся друг с другом с помощью трёх основных трансляций
Шесть параметров (а, b, с, α, β, γ) характеризуют внешнюю форму элементарной ячейки
В реальных кристаллических
структурах на местах узлов
пространственной решетки могут
находиться структурные единицы,
но узел пространственной решетки
не обязательно отождествлять
с материальной точкой

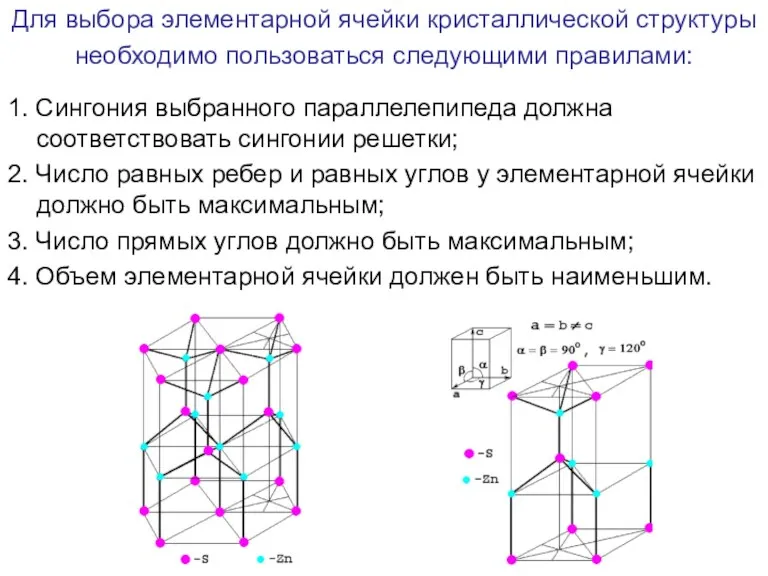
Для выбора элементарной ячейки кристаллической структуры необходимо пользоваться следующими правилами:
1. Сингония выбранного параллелепипеда должна соответствовать сингонии решетки;
2. Число равных ребер и равных углов у элементарной ячейки должно быть максимальным;
3. Число прямых углов должно быть максимальным;
4. Объем элементарной ячейки должен быть наименьшим.

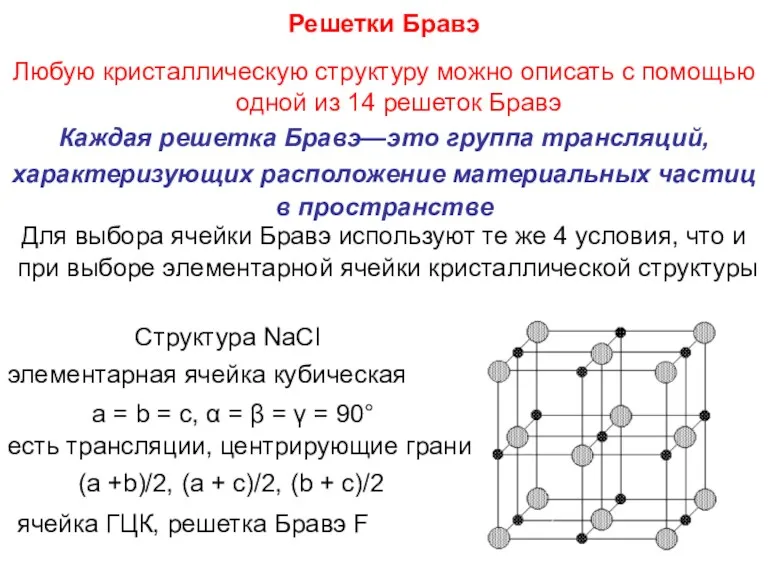
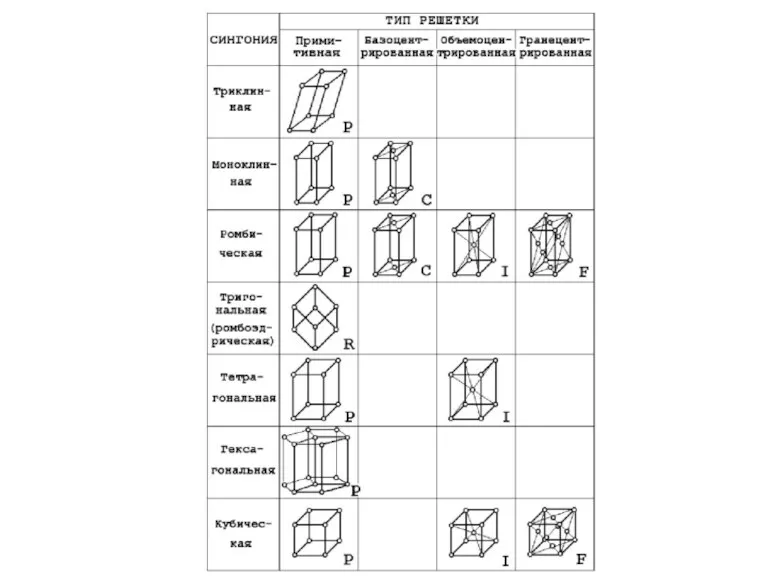
Решетки Бравэ
Любую кристаллическую структуру можно описать с помощью одной из 14 решеток Бравэ
Каждая решетка Бравэ—это группа трансляций,
характеризующих расположение материальных частиц
в пространстве
Для выбора ячейки Бравэ используют те же 4 условия, что и
при выборе элементарной ячейки кристаллической структуры
Структура NaCl
элементарная ячейка кубическая
a = b = c, α = β = γ = 90°
есть трансляции, центрирующие грани
(a +b)/2, (a + c)/2, (b + c)/2
ячейка ГЦК, решетка Бравэ F

Лекция 5
Элементы симметрии кристаллических структур
Сочетание трансляции с плоскостями m и поворотными
осями симметрии приводит к возникновению плоскостей
скользящего отражения и винтовых осей симметрии
Плоскостью скользящего отражения называется
совокупность совместно действующих плоскости
зеркального отражения и параллельной ей трансляции
(плоскости скользящего отражения: a, b, c, d, n)
Плоскости a, b, c
скольжение а/2, b/2, с/2
Плоскость d, скольжение
(а + b)/4, (а + с)/4, (b + с)/4
Плоскость n, скольжение
(а + b)/2, (а + с)/2, (b + с)/2

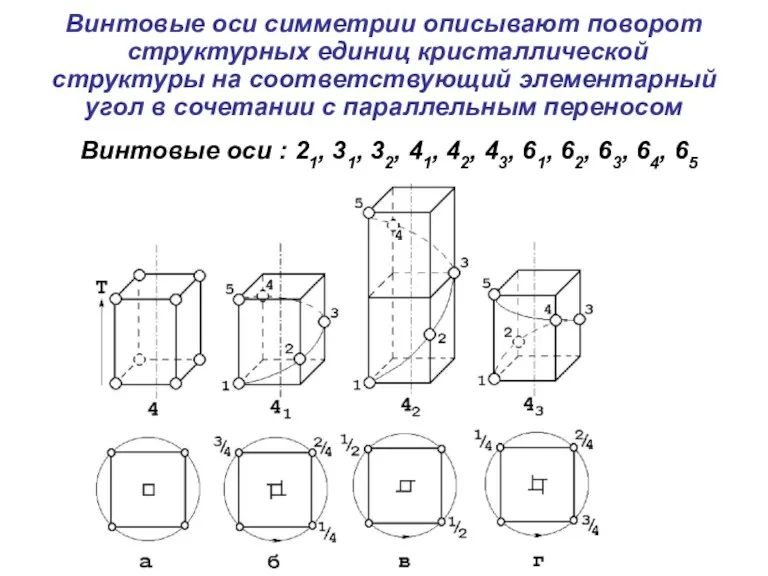
Винтовые оси симметрии описывают поворот
структурных единиц кристаллической структуры на соответствующий элементарный угол в сочетании с параллельным переносом
Винтовые оси : 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, 65

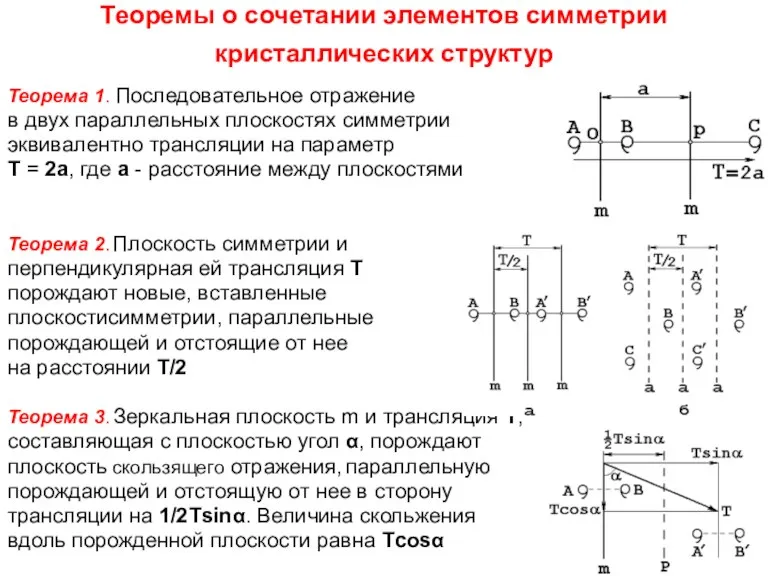
Теоремы о сочетании элементов симметрии кристаллических структур
Теорема 1. Последовательное отражение
в двух параллельных плоскостях симметрии
эквивалентно трансляции на параметр
Т = 2a, где а - расстояние между плоскостями
Теорема 2. Плоскость симметрии и
перпендикулярная ей трансляция Т
порождают новые, вставленные
плоскостисимметрии, параллельные
порождающей и отстоящие от нее
на расстоянии Т/2
Теорема 3. Зеркальная плоскость m и трансляция Т,
составляющая с плоскостью угол α, порождают
плоскость скользящего отражения, параллельную
порождающей и отстоящую от нее в сторону
трансляции на 1/2Тsinα. Величина скольжения
вдоль порожденной плоскости равна Тcosα

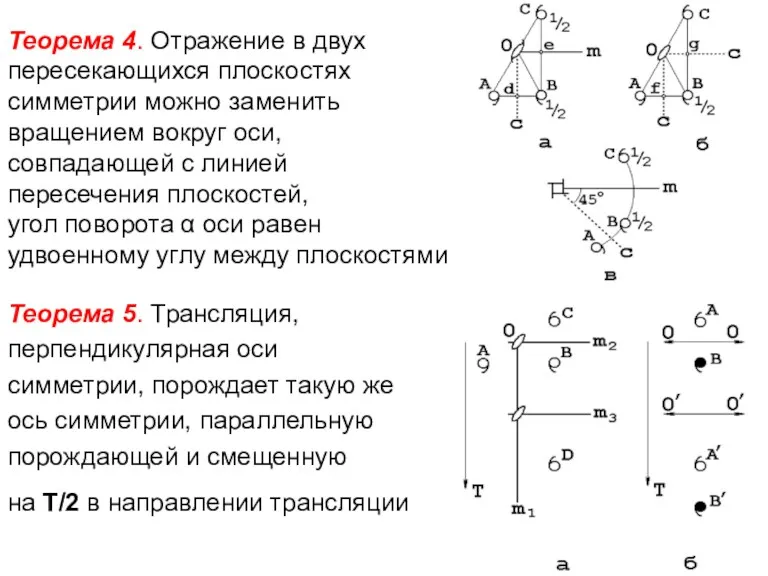
Теорема 4. Отражение в двух
пересекающихся плоскостях
симметрии можно заменить
вращением вокруг оси, совпадающей с линией
пересечения плоскостей,
угол поворота α оси равен
удвоенному углу между плоскостями
Теорема 5. Трансляция,
перпендикулярная оси
симметрии, порождает такую же
ось симметрии, параллельную
порождающей и смещенную
на Т/2 в направлении трансляции

Пространственные группы симметрии
Если к точечным группам симметрии (с учетом плоскостей скользящего отражения и винтовых осей) добавить группы трансляций (решетки Бравэ) получим 230 федоровских пространственных групп симметрии
Пример моноклинной сингонии. В моноклинную сингонию входят три точечных класса симметрии: 2, m и 2/m
Точечный
класс 2 →
→ Р-ячейка,
возникают
классы Р2 и P21
С-ячейка
С2 ≡ С21

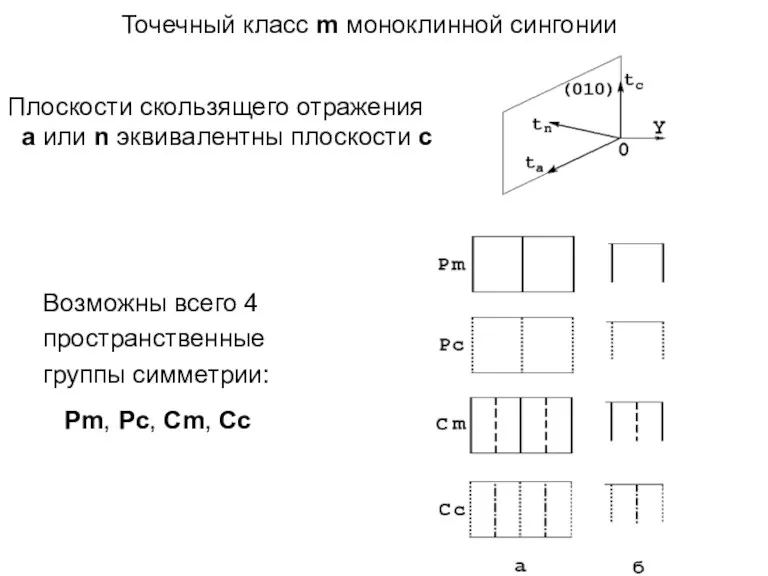
Точечный класс m моноклинной сингонии
Плоскости скользящего отражения
а или n эквивалентны плоскости с
Возможны всего 4
пространственные
группы симметрии:
Рm, Рс, Сm, Сс

Точечный класс 2/m моноклинной сингонии
Возможны 6 пространственных
групп симметрии:
Р2/m, Р2/с, С2/m, С2/с, Р21/m и Р21/с
В символе пространственной группы пишутся только
порождающие элементы симметрии. В международном
символе пространственной группы на первом месте всегда
стоит тип решетки Бравэ; далее - порождающие элементы
симметрии, каждый на определенном месте. Нарушение
порядка записи меняет смысл символа.

Лекция 6
Правильные системы точек
Правильной системой точек называется совокупность точек
(симметрично эквивалентных позиций), связанных между
собой элементами симметрии
Кратностью правильной системы точек называется число ее
точек, приходящихся на одну элементарную ячейку
Положение Кратность Позиция в межд.Табл.
1 (частная) 1 a
2 (частная) 1 b
3 (частная) 1 c
4 (частная) 1 d
5 (частная) 2 e
6 (частная) 2 f
7 (частная) 2 g
8 (частная) 2 h
9 (общая) 4 i
Для ПГС Рmm2

Базис структуры
Базисом кристаллической структуры называется
совокупность координат структурных единиц всех
правильных систем точек
Положение оси Z в элементарных ячейках Бравэ
(определяются только элементами симметрии
пространственной группы) относительно плоскости
чертежа для различных сингоний показано в
Международных таблицах
В Международных таблицах положение начала координат
относительно горизонтальных элементов симметрии
пространственной группы (если таковые имеются)
указано в долях трансляции с

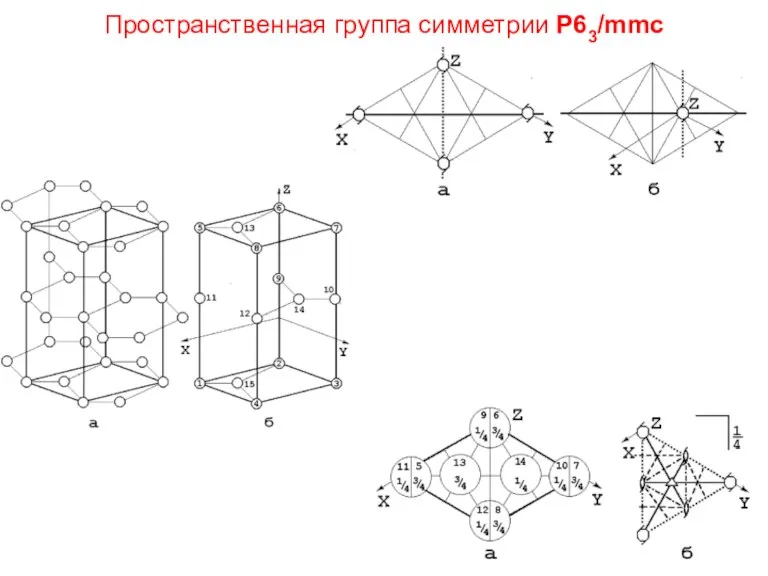
Пространственная группа симметрии Р63/mmс

Правильные системы точек в пространственных группах симметрии Р63/mmс и Р63mс

Понятие обратной решетки
Прямая решетка построена на векторах а, b, c (ai), а оси
обратной решетки (A, B, C)
[bc] = A , [ca] = B , [ab] = C
Можно нормировать оси обратной (bi)
в знаменателе стоит объем элементарной ячейки

Важнейшие свойства обратной решетки
Если провести радиус-вектор из начала координат в узел обратной решетки [[h1h2h3]]
, то:
1. радиус-вектор перпендикулярен к плоскости (h1h2h3)
прямой решетки;
2. по модулю обратно пропорционален межплоскостному
расстоянию

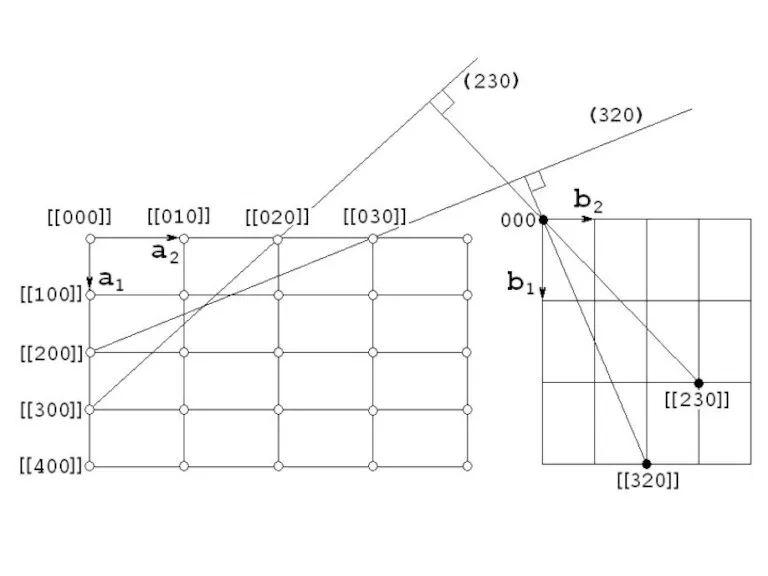
Проведем построение обратной решетки для плоской сетки
1. Выбираем начало координат для обратной решетки
2. Через начало координат проводим прямые,
перпендикулярные координатным плоскостям прямой
решетки – координатные оси обратной решетки
3. Откладываем на этих осях от начала координат
единичные векторы обратной решетки b1 и b2.
4. Для построения узла обратной решетки,
соответствующего плоскости (hkl) прямой решетки (например
320 или 230 ) откладываем «h» единиц вдоль b1 , «k» единиц
вдоль b2 и «l» единиц вдоль b3 (в нашем случае l = 0)

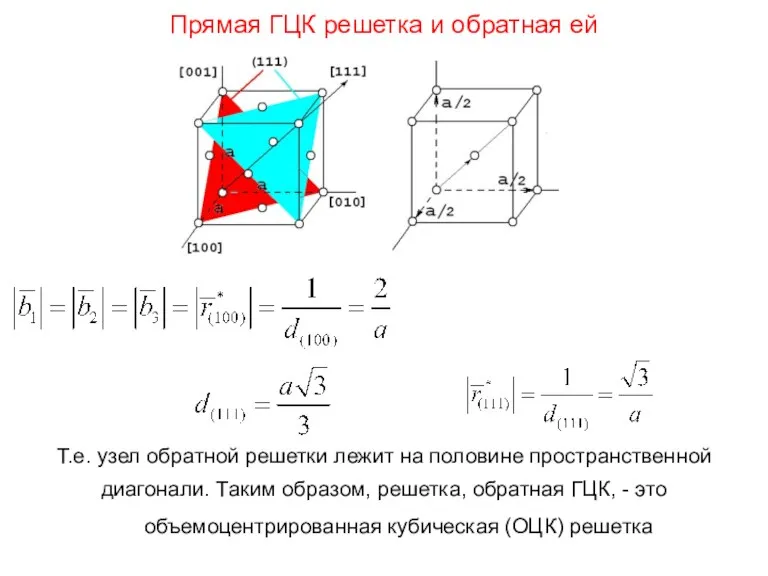
Прямая ГЦК решетка и обратная ей
Т.е. узел обратной решетки лежит на половине пространственной
диагонали. Таким образом, решетка, обратная ГЦК, - это объемоцентрированная кубическая (ОЦК) решетка

Раздел 3
Элементы кристаллохимии и дефекты в кристаллах
Лекция 8
Типы химической связи в кристаллах
Кристаллохимия - это теория, содержащая ряд
закономерностей, определяющих строение
кристаллических структур
Основные типы химической связи:
1. Ионная (гетерополярная) связь;
2. Ковалентная (гомеополярная) связь;
3. Металлическая связь;
4. Ван-дер-ваальсова связь;
5. Водородная связь.

Ионная связь
Потенциал ионизации - энергия, затрачиваемая на отрыв
валентных электронов от атома катиона
Атом металлоида, присоединяя электроны, выделяет энергию называемую сродством к электрону
Энергию ионной химической связи (U) можно определить как
сумму потенциала кулоновского взаимодействия (-Uk),
потенциала ионизации и сродства к электрону
Структуры ионных кристаллов делят на две группы:
Изодесмические структуры, образуют анионы F-, Cl-, Br-, I-, OH-, Se2-, Тe2-,
P3- и др., не являющиеся изолированными комплексами, и катионы Li+, Na+
K+ , Ag+, Mg2+, Al3+ и др. (NaCl, CaF2, Fe2O3, BaTiO3, Y3Al5O15)
Анизодесмические и мезодесмические структуры содержат структурные,
изолированные группы, являющиеся комплексными ионами (IO3)-, (MnO4)-,
(CrO4)-, (MoO4)-, (WO4)- - силикаты, бораты и германаты

Ковалентная связь
Сближающиеся атомы создают законченные электронные
оболочки, обобществляя валентные электроны
(с антипараллельными спинами ) соседей
Ковалентная связь, создающаяся спаренными электронами,
может возникать и в тех случаях, когда у одного атома
(донора) есть лишние электроны, а у другого (акцептора)
незаполненные - свободные, не занятые электронами
орбитали. Общее число электронов может быть таким, что
они образуют завершенные оболочки для каждого атома,
как например, в соединениях III и V групп или II и VI групп

Ионно-ковалентная связь
Для чисто ковалентной связи характерно одинаковое
распределение электронной плотности между атомами (Si,
Ge, C).
Если кристалл состоит из разных элементов, то связь между
ними имеет ту или иную долю ионности (или ковалентности).
Доля ионности в связи определяется электроотрицательностью атома.
Электроотрицательность - способность атома к присоединению электрона.
Степень ионности меньше единицы означает, что валентные
электроны не полностью принадлежат аниону, частично
локализованы у катиона и заряды отрицательного аниона и
положительного катиона меньше номинальной валентности.
Понятие эффективного заряда иона, как Z=ε n

Металлическая связь
Для металлической связи характерно равномерное
распределение валентных электронов между всеми атомами.
При металлической связи общим валентным электронам
не нужна дополнительная энергия для отрыва от своего
атома, т.к. они свободны и в равной мере принадлежат всем
атомам кристалла.
Это означает, что в металлах отсутствует зона запрещенных
энергий между валентной зоной и зоной проводимости и эти
зоны сливаются.
Связь обеспечивается взаимодействием положительных ядер остова с электронным газом.

Слабая (ван-дер-ваальсова) связь
Слабые связи наблюдаются между атомами с замкнутыми
электронными оболочками (благородные газы) или между
молекулами, сильные (ковалентные) связи внутри которых
полностью насыщены.
Атомные радиусы
Величины атомных радиусов зависят от номера Z атома и его
положения в периодической системе элементов.
Рассмотрение ионных радиусов, основанное на
геометрических представлениях о построении
кристаллических решеток определяет т.н. "классические"
ионные радиусы.
"физические" ионные радиусы определяются с учетом
распределение электронной плотности у аниона и катиона

Координационные числа и многогранники
Симметрия кристалла подчиняется принципу Кюри, т.е.
симметрия структурных единиц включает симметрию
кристалла и группа симметрии кристалла является
подгруппой симметрии структурных единиц, образующих
кристалл.
Для данного атома под координацией понимают тип соседей, число соседей и расстояния до соседей.
Ближайшие соседи образуют первую координационную
сферу.
Если соединить центры атомов координационной сферы
прямыми, то такие прямые являются ребрами
многогранника (полиэдра), называемого координационным
полиэдром (многогранником).

Типы координационных полиэдров

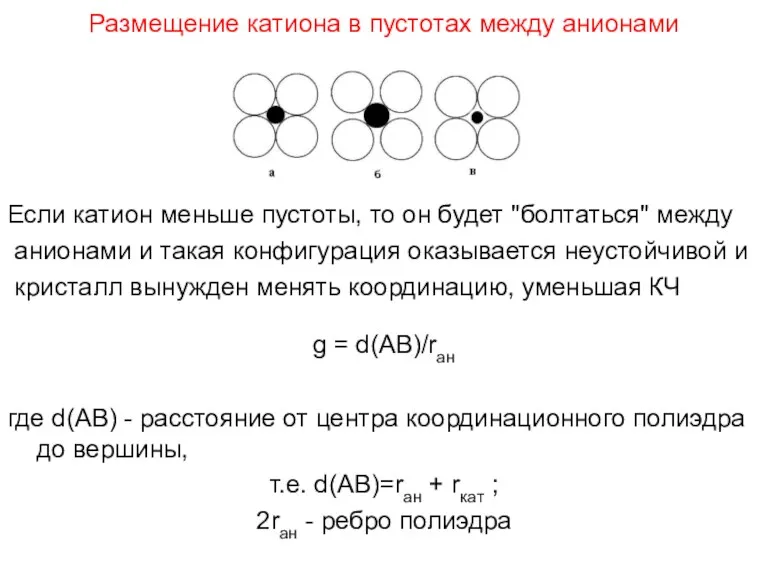
Размещение катиона в пустотах между анионами
Если катион меньше пустоты, то он будет "болтаться" между
анионами и такая конфигурация оказывается неустойчивой и
кристалл вынужден менять координацию, уменьшая КЧ
g = d(AB)/rан
где d(AB) - расстояние от центра координационного полиэдра до вершины,
т.е. d(AB)=rан + rкат ;
2rан - ребро полиэдра

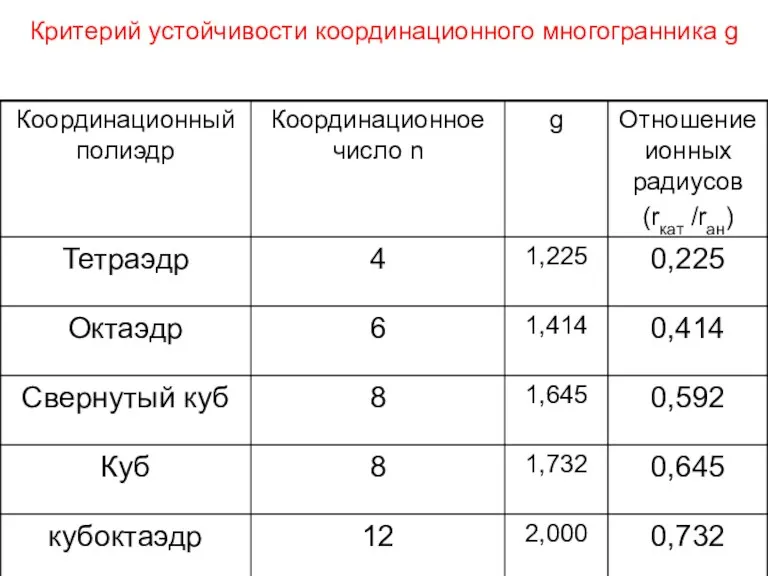
Критерий устойчивости координационного многогранника g

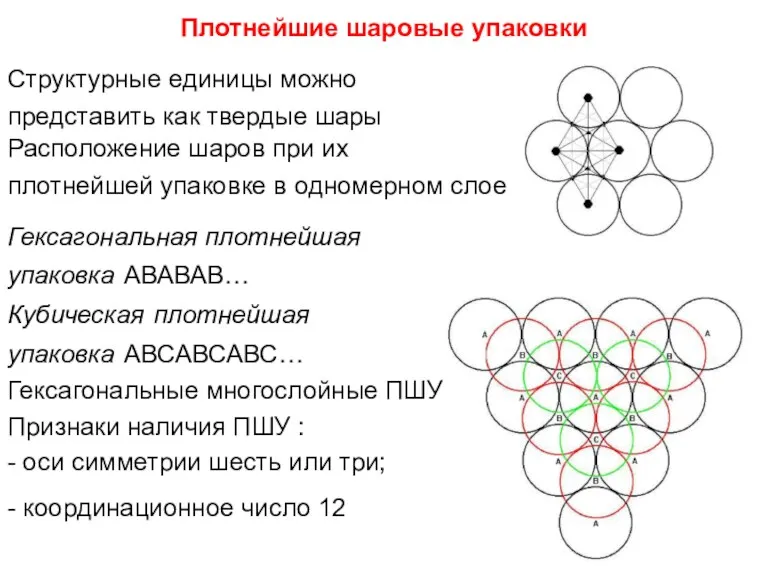
Плотнейшие шаровые упаковки
Структурные единицы можно
представить как твердые шары
Расположение шаров при их
плотнейшей упаковке в одномерном слое
Гексагональная плотнейшая
упаковка АВАВАВ…
Кубическая плотнейшая
упаковка АВСАВСАВС…
Гексагональные многослойные ПШУ
Признаки наличия ПШУ :
- оси симметрии шесть или три;
- координационное число 12

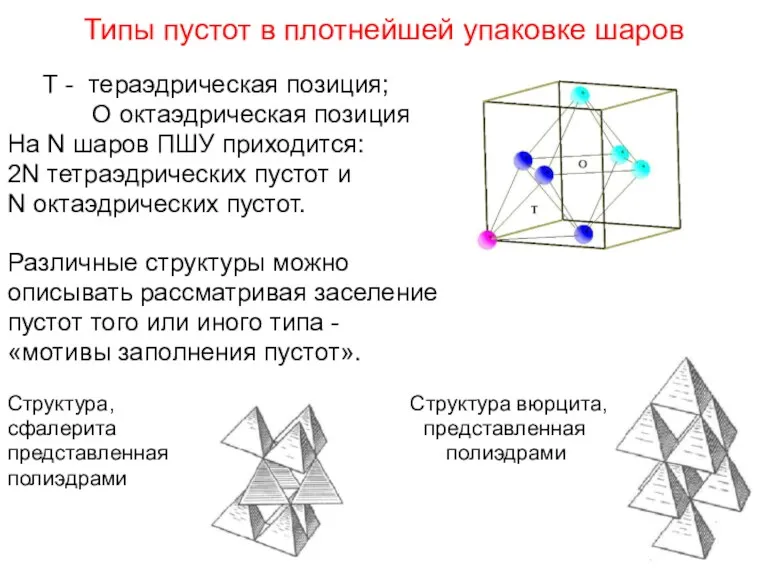
Типы пустот в плотнейшей упаковке шаров
Т - тераэдрическая позиция;
О октаэдрическая позиция
На N шаров ПШУ приходится:
2N тетраэдрических пустот и
N октаэдрических пустот.
Различные структуры можно
описывать рассматривая заселение
пустот того или иного типа -
«мотивы заполнения пустот».
Структура, Структура вюрцита,
сфалерита представленная
представленная полиэдрами
полиэдрами

Изоморфизм
Атомы с одинаковыми валентностями, типом связи,
поляризацией с близкими атомными радиусами могут замещать друг друга в кристаллической решетке, образуя
кристаллы переменного состава (явление – изоморфизм).
Т.е. близкие, но не тождественные по составу изоморфные
вещества кристаллизуются в одинаковых формах
(BaTiO3, PbTiO3, KNbO3).
В изоморфных твердых растворах замещения физические
свойства могут изменятся непрерывно в зависимости от
концентрации компонентов.

Полиморфизм
Способность некоторых веществ существовать в нескольких
кристаллических фазах, отличающихся по симметрии
структуры и по свойствам.
Каждая полиморфная модификация вещества стабильна в
своей области температур и давлений.
Фазовое состояние вещества удобно характеризовать
р-Т диаграммой.
Изменение кристаллической структуры при полиморфных
превращениях может проходить различными путями.
Полиморфные превращения могут относится как к переходам
I рода, так и II.

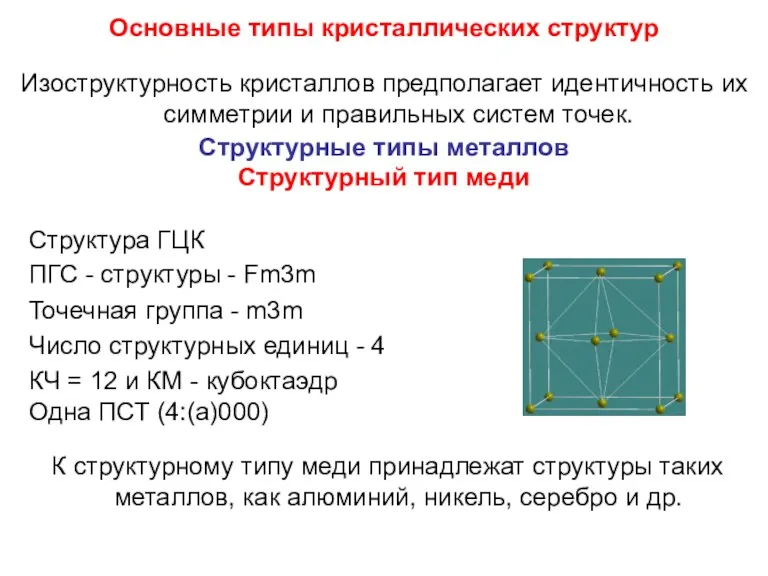
Основные типы кристаллических структур
Изоструктурность кристаллов предполагает идентичность их симметрии и правильных систем точек.
Структурные типы металлов
Структурный тип меди
Структура ГЦК
ПГС - структуры - Fm3m
Точечная группа - m3m
Число структурных единиц - 4
КЧ = 12 и КМ - кубоктаэдр
Одна ПСТ (4:(а)000)
К структурному типу меди принадлежат структуры таких металлов, как алюминий, никель, серебро и др.

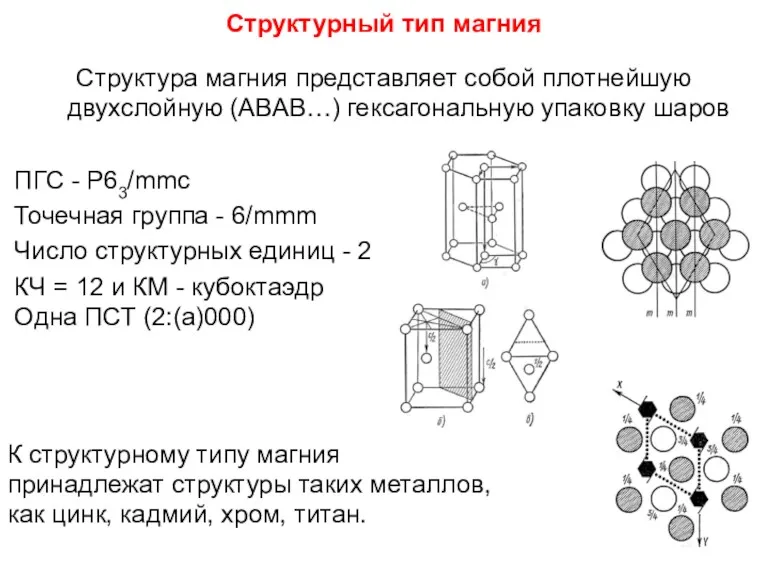
Структурный тип магния
Структура магния представляет собой плотнейшую двухслойную (АВАВ…) гексагональную упаковку шаров
ПГС - Р63/mmc
Точечная группа - 6/mmm
Число структурных единиц - 2
КЧ = 12 и КМ - кубоктаэдр
Одна ПСТ (2:(а)000)
К структурному типу магния
принадлежат структуры таких металлов,
как цинк, кадмий, хром, титан.

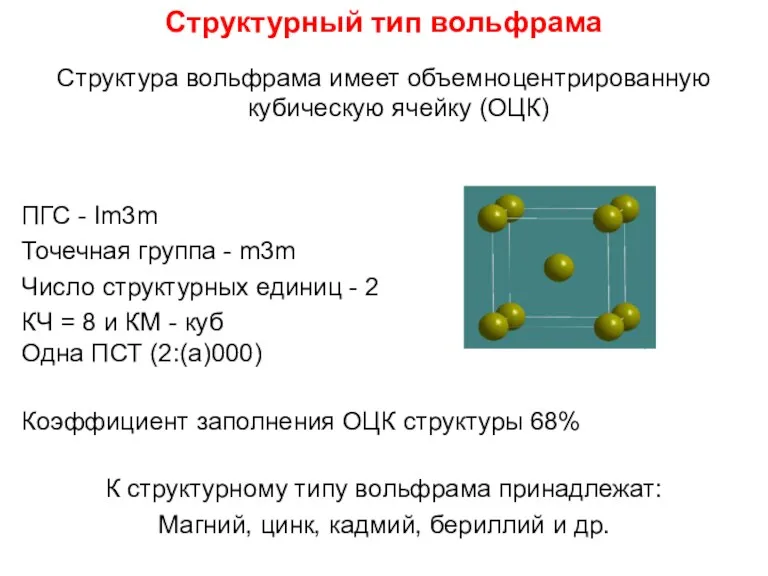
Структурный тип вольфрама
Структура вольфрама имеет объемноцентрированную кубическую ячейку (ОЦК)
ПГС - Im3m
Точечная группа - m3m
Число структурных единиц - 2
КЧ = 8 и КМ - куб
Одна ПСТ (2:(а)000)
Коэффициент заполнения ОЦК структуры 68%
К структурному типу вольфрама принадлежат:
Магний, цинк, кадмий, бериллий и др.

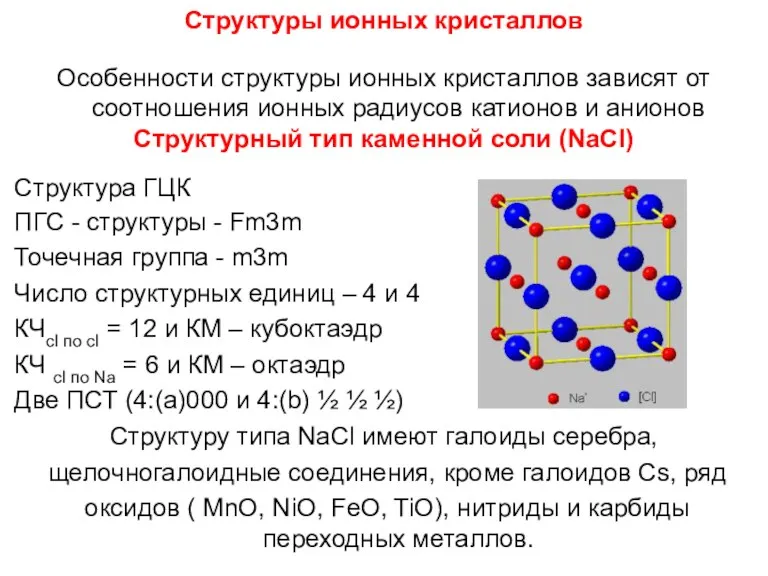
Структуры ионных кристаллов
Особенности структуры ионных кристаллов зависят от соотношения ионных радиусов катионов и анионов
Структурный тип каменной соли (NaCl)
Структура ГЦК
ПГС - структуры - Fm3m
Точечная группа - m3m
Число структурных единиц – 4 и 4
КЧcl по cl = 12 и КМ – кубоктаэдр
КЧ cl по Na = 6 и КМ – октаэдр
Две ПСТ (4:(а)000 и 4:(b) ½ ½ ½)
Структуру типа NaCl имеют галоиды серебра,
щелочногалоидные соединения, кроме галоидов Cs, ряд
оксидов ( MnO, NiO, FeO, TiO), нитриды и карбиды переходных металлов.

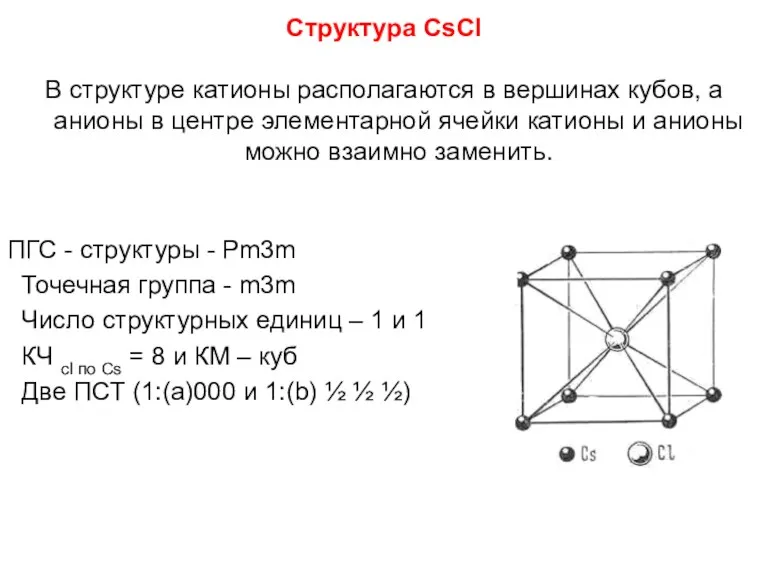
Структура CsCl
В структуре катионы располагаются в вершинах кубов, а анионы в центре элементарной ячейки катионы и анионы можно взаимно заменить.
ПГС - структуры - Рm3m
Точечная группа - m3m
Число структурных единиц – 1 и 1
КЧ cl по Cs = 8 и КМ – куб
Две ПСТ (1:(а)000 и 1:(b) ½ ½ ½)

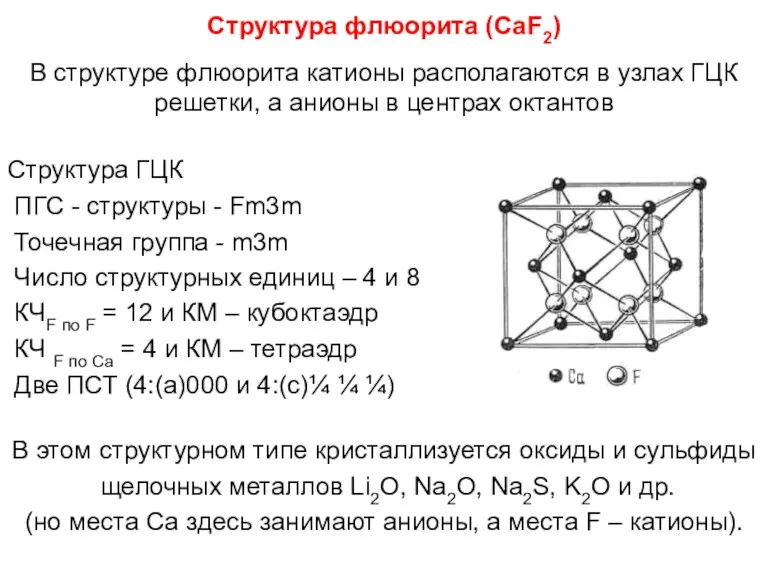
Структура флюорита (СaF2)
В структуре флюорита катионы располагаются в узлах ГЦК
решетки, а анионы в центрах октантов
Структура ГЦК
ПГС - структуры - Fm3m
Точечная группа - m3m
Число структурных единиц – 4 и 8
КЧF по F = 12 и КМ – кубоктаэдр
КЧ F по Ca = 4 и КМ – тетраэдр
Две ПСТ (4:(а)000 и 4:(с)¼ ¼ ¼)
В этом структурном типе кристаллизуется оксиды и сульфиды
щелочных металлов Li2O, Na2O, Na2S, K2O и др.
(но места Са здесь занимают анионы, а места F – катионы).

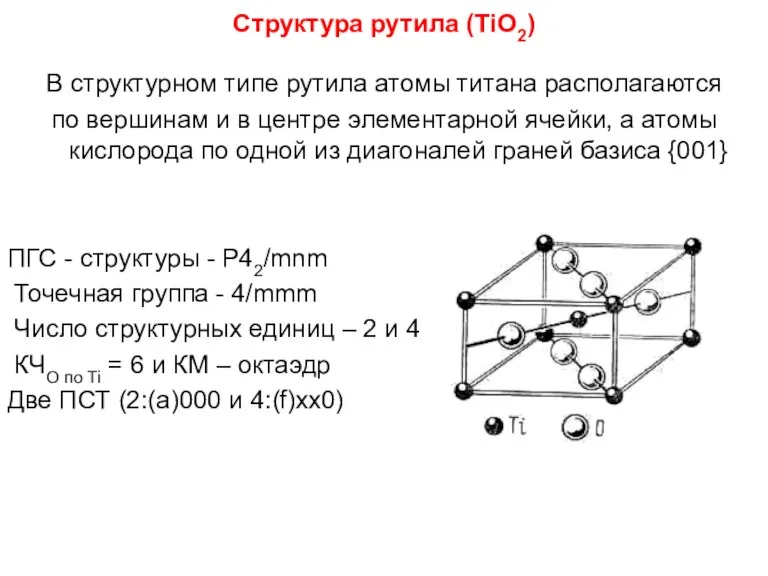
Структура рутила (TiO2)
В структурном типе рутила атомы титана располагаются
по вершинам и в центре элементарной ячейки, а атомы кислорода по одной из диагоналей граней базиса {001}
ПГС - структуры - Р42/mnm
Точечная группа - 4/mmm
Число структурных единиц – 2 и 4
КЧO по Ti = 6 и КМ – октаэдр
Две ПСТ (2:(а)000 и 4:(f)xx0)

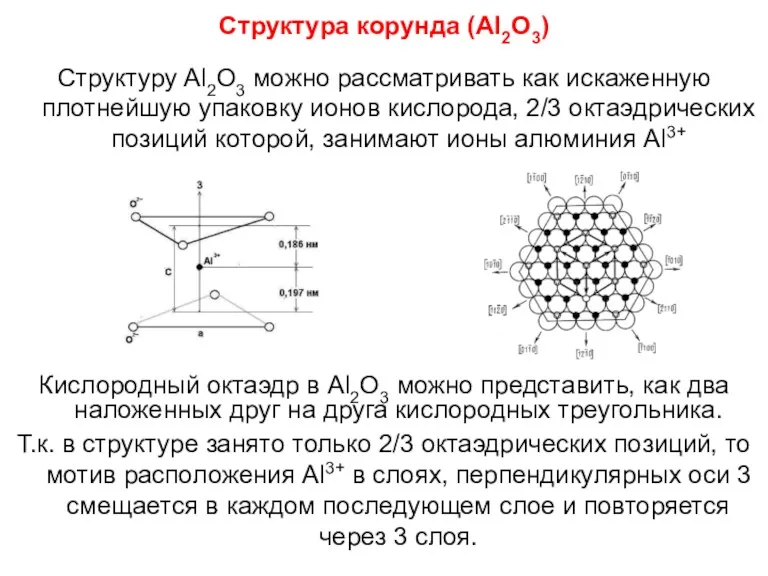
Структура корунда (Al2O3)
Структуру Al2O3 можно рассматривать как искаженную плотнейшую упаковку ионов кислорода, 2/3 октаэдрических позиций которой, занимают ионы алюминия Al3+
Кислородный октаэдр в Al2O3 можно представить, как два наложенных друг на друга кислородных треугольника.
Т.к. в структуре занято только 2/3 октаэдрических позиций, то мотив расположения Al3+ в слоях, перпендикулярных оси 3 смещается в каждом последующем слое и повторяется через 3 слоя.

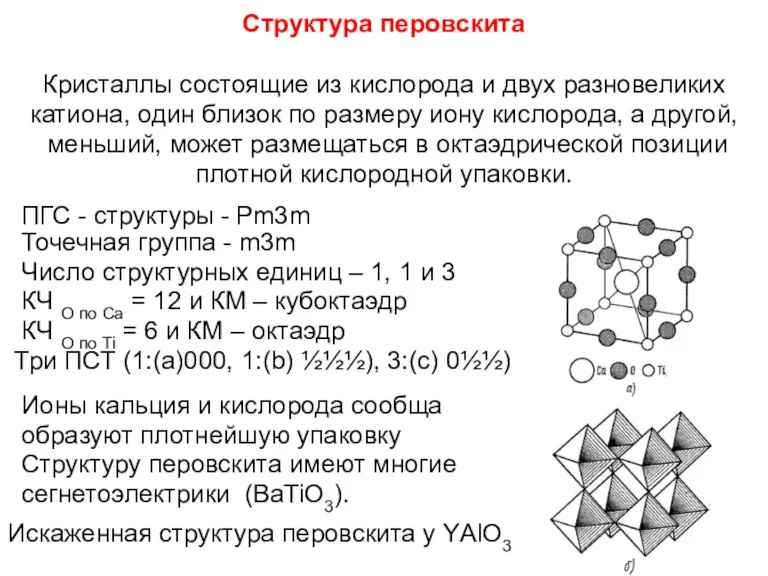
Структура перовскита
Кристаллы состоящие из кислорода и двух разновеликих
катиона, один близок по размеру иону кислорода, а другой,
меньший, может размещаться в октаэдрической позиции
плотной кислородной упаковки.
ПГС - структуры - Рm3m
Точечная группа - m3m
Число структурных единиц – 1, 1 и 3
КЧ О по Cа = 12 и КМ – кубоктаэдр
КЧ О по Ti = 6 и КМ – октаэдр
Три ПСТ (1:(а)000, 1:(b) ½½½), 3:(с) 0½½)
Ионы кальция и кислорода сообща
образуют плотнейшую упаковку
Структуру перовскита имеют многие
сегнетоэлектрики (BaTiO3).
Искаженная структура перовскита у YАlO3

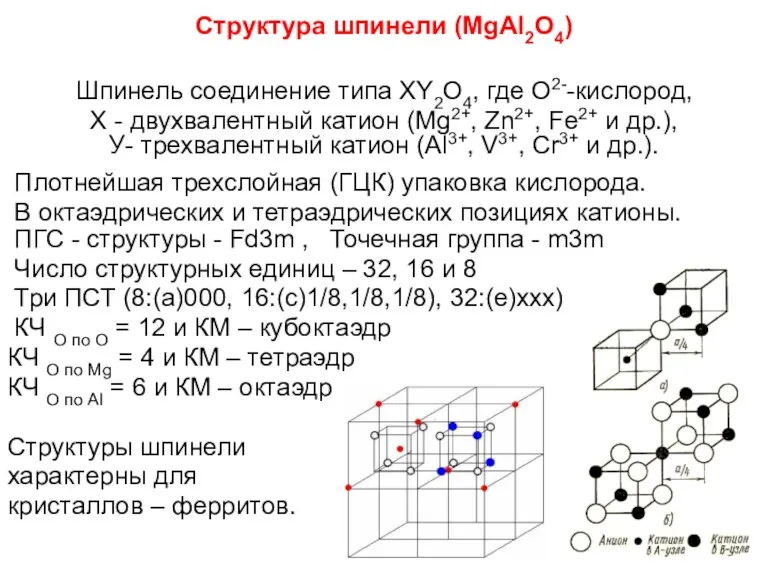
Структура шпинели (MgAl2О4)
Шпинель соединение типа XY2O4, где О2--кислород,
Х - двухвалентный катион (Mg2+, Zn2+, Fe2+ и др.),
У- трехвалентный катион (Al3+, V3+, Cr3+ и др.).
Плотнейшая трехслойная (ГЦК) упаковка кислорода.
В октаэдрических и тетраэдрических позициях катионы.
ПГС - структуры - Fd3m , Точечная группа - m3m
Число структурных единиц – 32, 16 и 8
Три ПСТ (8:(а)000, 16:(с)1/8,1/8,1/8), 32:(е)ххх)
КЧ О по О = 12 и КМ – кубоктаэдр
КЧ О по Mg = 4 и КМ – тетраэдр
КЧ О по Al = 6 и КМ – октаэдр
Структуры шпинели
характерны для
кристаллов – ферритов.

Структура гранатов
Естественные гранаты - силикаты с химической формулой М3М2[SiO4]3, где M2+ - Mg, Ca, Mn, Fe и M3+ - Al, Fe, Cr, Ti.
ПГС - структуры - Ia3d
Точечная группа - m3m
Число структурных единиц (Z = 8):
М2+ - 24, М3+ - 16 и Si4+ - 24
Ионы кислорода в гранате образуют
решетку, состоящую из трех типов
координационных многогранников:
тетраэдров, октаэдров и додекаэдров.
Структуру граната можно представить,
как цепочки октаэдров в направлениях <111>
и цепочки чередующихся додекаэдров и
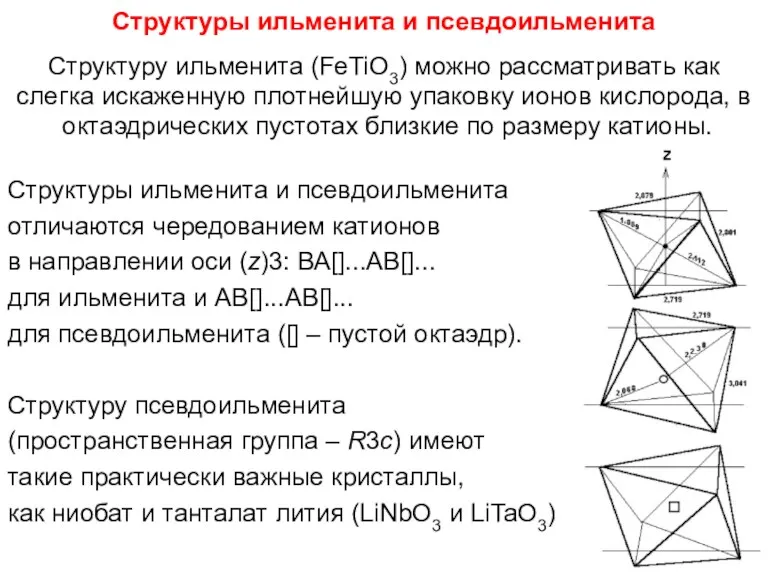
тетраэдров в направлениях <100>.

Структуры ильменита и псевдоильменита
Структуру ильменита (FeTiO3) можно рассматривать как
слегка искаженную плотнейшую упаковку ионов кислорода, в
октаэдрических пустотах близкие по размеру катионы.
Структуры ильменита и псевдоильменита
отличаются чередованием катионов
в направлении оси (z)3: ВА[]...AB[]...
для ильменита и AB[]...AB[]...
для псевдоильменита ([] – пустой октаэдр).
Структуру псевдоильменита
(пространственная группа – R3c) имеют
такие практически важные кристаллы,
как ниобат и танталат лития (LiNbO3 и LiTaO3)

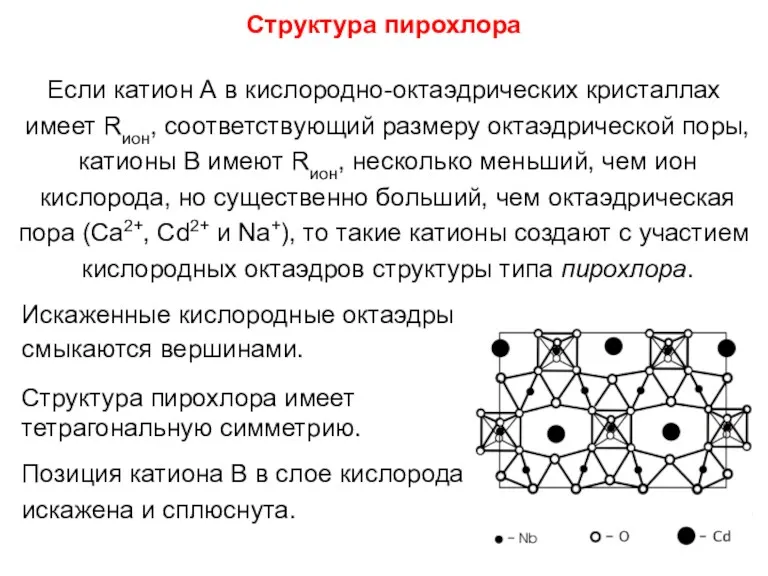
Структура пирохлора
Если катион А в кислородно-октаэдрических кристаллах
имеет Rион, соответствующий размеру октаэдрической поры,
катионы В имеют Rион, несколько меньший, чем ион
кислорода, но существенно больший, чем октаэдрическая
пора (Са2+, Cd2+ и Na+), то такие катионы создают с участием
кислородных октаэдров структуры типа пирохлора.
Искаженные кислородные октаэдры
смыкаются вершинами.
Структура пирохлора имеет
тетрагональную симметрию.
Позиция катиона В в слое кислорода
искажена и сплюснута.

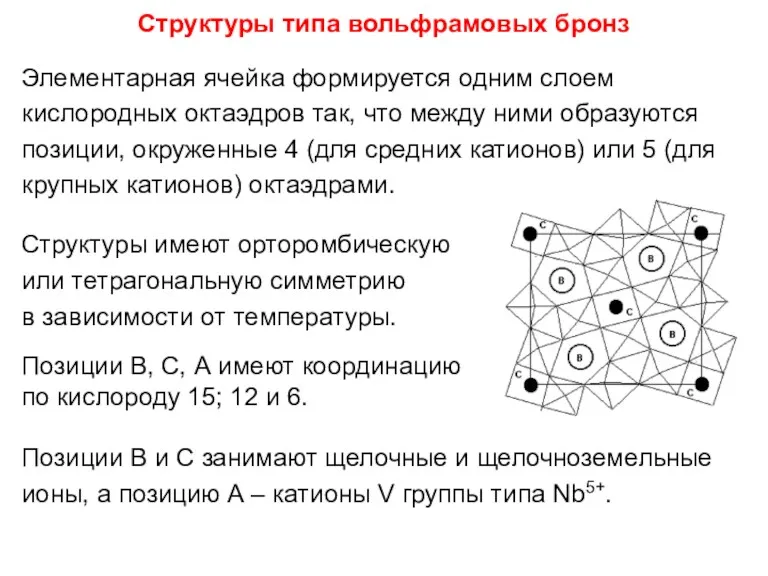
Структуры типа вольфрамовых бронз
Элементарная ячейка формируется одним слоем
кислородных октаэдров так, что между ними образуются
позиции, окруженные 4 (для средних катионов) или 5 (для
крупных катионов) октаэдрами.
Структуры имеют орторомбическую
или тетрагональную симметрию
в зависимости от температуры.
Позиции В, С, А имеют координацию
по кислороду 15; 12 и 6.
Позиции В и С занимают щелочные и щелочноземельные
ионы, а позицию А – катионы V группы типа Nb5+.

Ковалентные структуры
Структура графита
При построении ковалентных структур основную роль играет геометрия связей (взаимное направление связей).
Химическую связь атомов С создают один S и три Р
электронов, поэтому у каждого атома С одна связь не
эквивалентна трем другим. В структуре графита каждый атом
связан прочными ковалентными связями с тремя другими в плоские сетки (слои), состоящие из гексагонов.
ПГС - Р63/mmc
Точечная группа - 6/mmm
Число структурных единиц – 4
КЧ = 3 и КМ – треугольник
Две ПСТ (2:(b)00¼ и 2:(с)1/3 2/3 ¼)

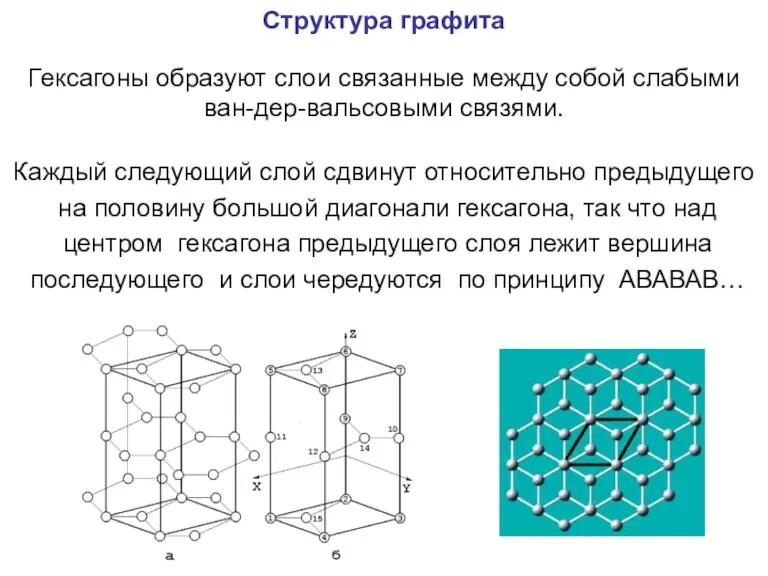
Структура графита
Гексагоны образуют слои связанные между собой слабыми
ван-дер-вальсовыми связями.
Каждый следующий слой сдвинут относительно предыдущего
на половину большой диагонали гексагона, так что над
центром гексагона предыдущего слоя лежит вершина
последующего и слои чередуются по принципу АВАВАВ…

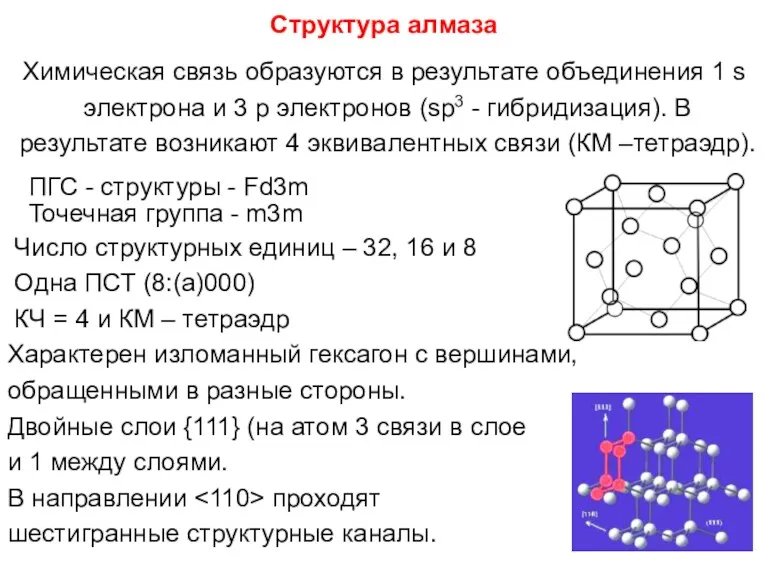
Структура алмаза
Химическая связь образуются в результате объединения 1 s
электрона и 3 p электронов (sp3 - гибридизация). В
результате возникают 4 эквивалентных связи (КМ –тетраэдр).
ПГС - структуры - Fd3m
Точечная группа - m3m
Число структурных единиц – 32, 16 и 8
Одна ПСТ (8:(а)000)
КЧ = 4 и КМ – тетраэдр
Характерен изломанный гексагон с вершинами,
обращенными в разные стороны.
Двойные слои {111} (на атом 3 связи в слое
и 1 между слоями.
В направлении <110> проходят
шестигранные структурные каналы.

Алмазоподобные структуры
Алмазоподобными обычно называют структуры :
- Каждый атом связан с соседями 4 равноценными связями (по два электрона), каждый атом имеет законченную 8-и электронную оболочку (соединения III и IV групп GaAs, InSb, InAs и др., II и VI ZnS, CdS, CdSe, и др.)
- Каждый атом имеет тетраэдрическое окружение атомами другого типа.
- Наличие характерного изломанного гексагона.
Алмазоподобные структуры состоят
из плотноупакованных слоев,
построенных по алмазному типу.
Возможно два типа чередования
слоев, что создает два типа
алмазоподобных структур:
сфалерит и вюрцит.

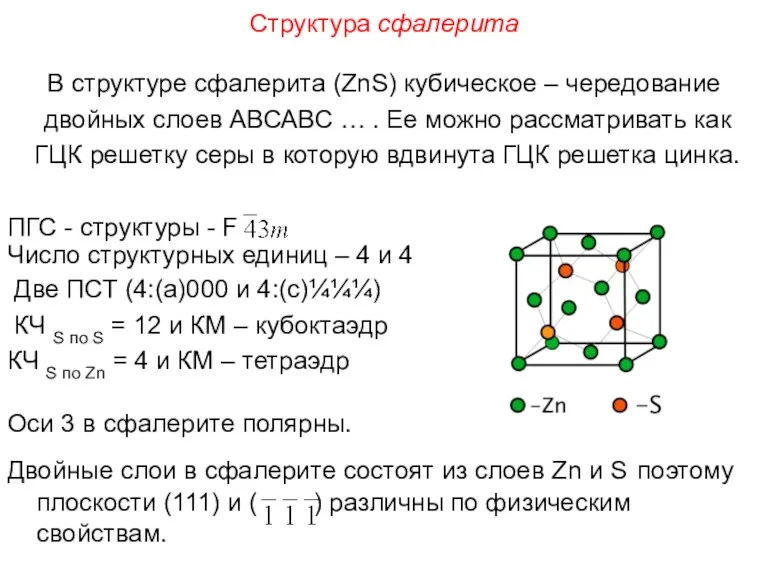
Структура сфалерита
В структуре сфалерита (ZnS) кубическое – чередование
двойных слоев АВСАВС … . Ее можно рассматривать как
ГЦК решетку серы в которую вдвинута ГЦК решетка цинка.
ПГС - структуры - F
Число структурных единиц – 4 и 4
Две ПСТ (4:(а)000 и 4:(с)¼¼¼)
КЧ S по S = 12 и КМ – кубоктаэдр
КЧ S по Zn = 4 и КМ – тетраэдр
Оси 3 в сфалерите полярны.
Двойные слои в сфалерите состоят из слоев Zn и S поэтому плоскости (111) и ( ) различны по физическим свойствам.

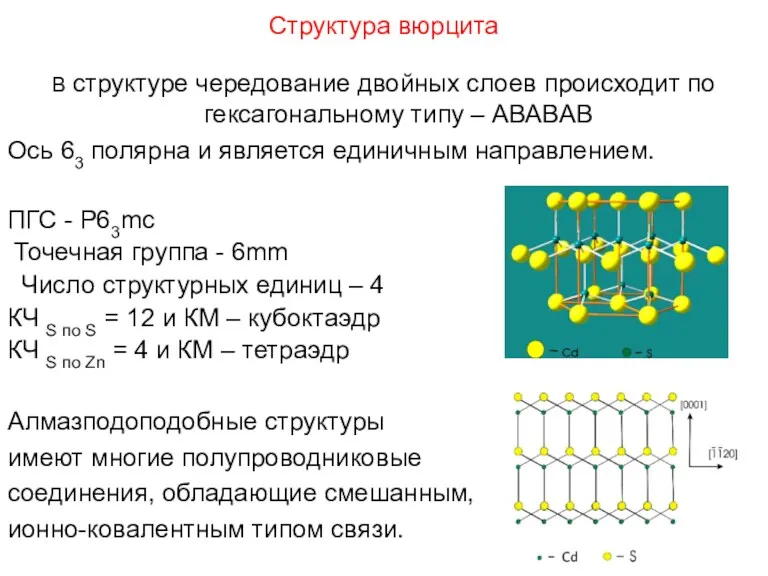
Структура вюрцита
В структуре чередование двойных слоев происходит по гексагональному типу – АВАВАВ
Ось 63 полярна и является единичным направлением.
ПГС - Р63mc
Точечная группа - 6mm
Число структурных единиц – 4
КЧ S по S = 12 и КМ – кубоктаэдр
КЧ S по Zn = 4 и КМ – тетраэдр
Алмазподоподобные структуры
имеют многие полупроводниковые
соединения, обладающие смешанным,
ионно-ковалентным типом связи.

Дефекты в кристаллах
Лекция 9
Классы дефектов в кристаллах по геометрическим признакам:
Точечные (нульмерные) дефекты. Размеры этих дефектов во всех трех измерениях не превышают нескольких межатомных расстояний (вакансии, атомы в междуузлиях, примеси и комплексы точечных дефектов).
2. Линейные (одномерные) дефекты. Эти дефекты в одном направлении простираются на расстояния, на много большее чем параметр элементарной ячейки (дислокации и цепочки точечных дефектов).
3. Плоские или поверхностные (двумерные) дефекты (поверхность кристалла, границы зерен и двойников, межфазные границы, доменные стенки).
4. Объемные (трехмерные) дефекты (микропустоты, трещины, включения другой фазы)

Понятие о дислокации
Дислокация линейный дефект и неравновесный. Изменение
свободной энергии, связанное с ее образованием, равно
энергии образования, энтропийный член мал и является
величиной положительной.
Дислокации образуются в следствие:
- наличия градиента температуры при росте и последующим охлаждении кристалла;
- внутренних упругих напряжений при легировании;
- радиационного облучения;
- несовпадения параметров решеток подложек и пленок при наращивании.
Наиболее теоретически и экспериментально изучен вопрос
о возникновении дислокаций при пластической деформации.

Движение дислокации в решетке происходит
много легче, чем одновременный сдвиг одной
части кристалла относительно другой
Дислокация задается тремя
векторами (b, l, η).
Плоскость скольжения (S).
Площадь, на которой прошло
скольжение (А), ограничено
контуром L (ограничивает область сдвига).
Линия дислокации (l) это единичный вектор, совпадающий
по направлению с касательной к L в данной точке (dl).
Направление выбирается произвольно (как направление
обхода по линии дислокации), но при рассмотрении данной
дислокации в дальнейшем не должно меняться.

Вектор мощности дислокации (b) - вектор Бюргерса, вектор, замыкающий контур Бюргерса, (произвольный замкнутый контур в совершенном кристалле).
Вектор Бюргерса является инвариантной характеристикой
дислокации.
Вектор смещения движущейся дислокации (η).
По взаимному расположению векторов b и l различают:
- если b перпендикулярен l - краевая дислокация;
- если b параллелен l - винтовая дислокация;
- если между b и l угол φ (φ не равен 0 или 90) – смешанная
дислокация (краевая компонента которой с вектором
Бюргерса bcosφ и винтовая компонента
с вектором Бюргерса bsinφ)

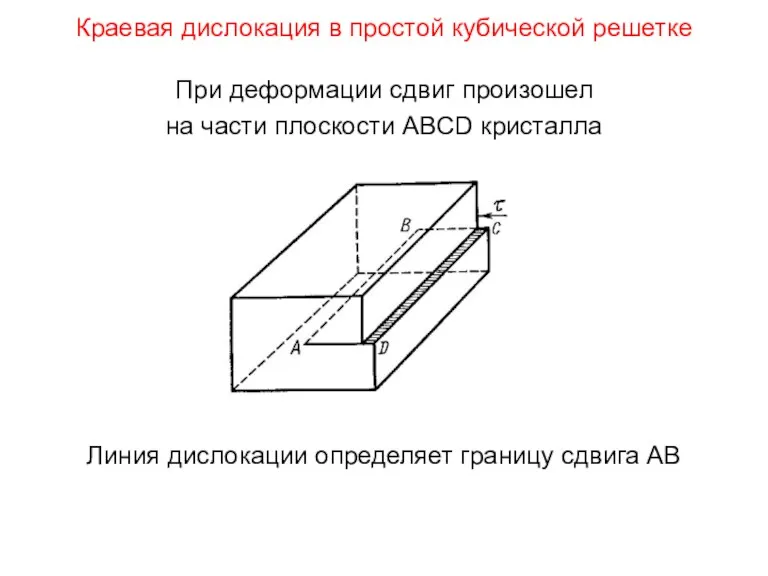
Краевая дислокация в простой кубической решетке
При деформации сдвиг произошел
на части плоскости АBCD кристалла
Линия дислокации определяет границу сдвига АВ

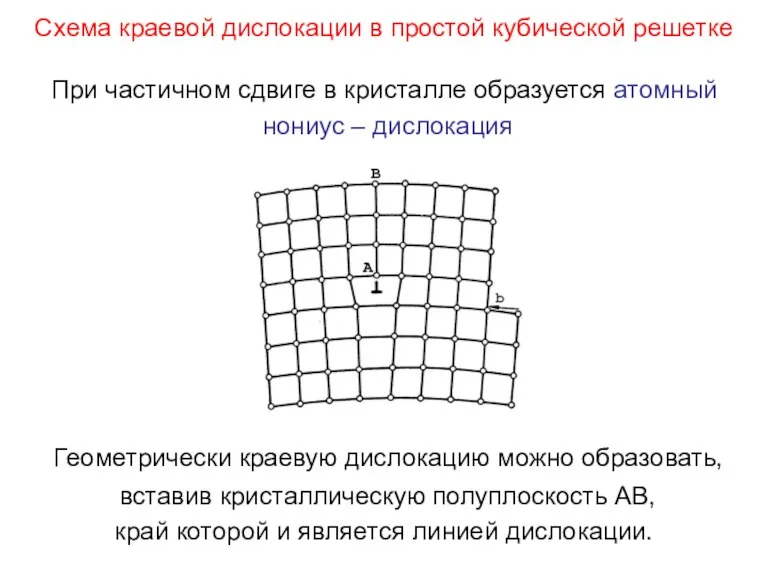
Схема краевой дислокации в простой кубической решетке
При частичном сдвиге в кристалле образуется атомный
нониус – дислокация
Геометрически краевую дислокацию можно образовать,
вставив кристаллическую полуплоскость АВ,
край которой и является линией дислокации.

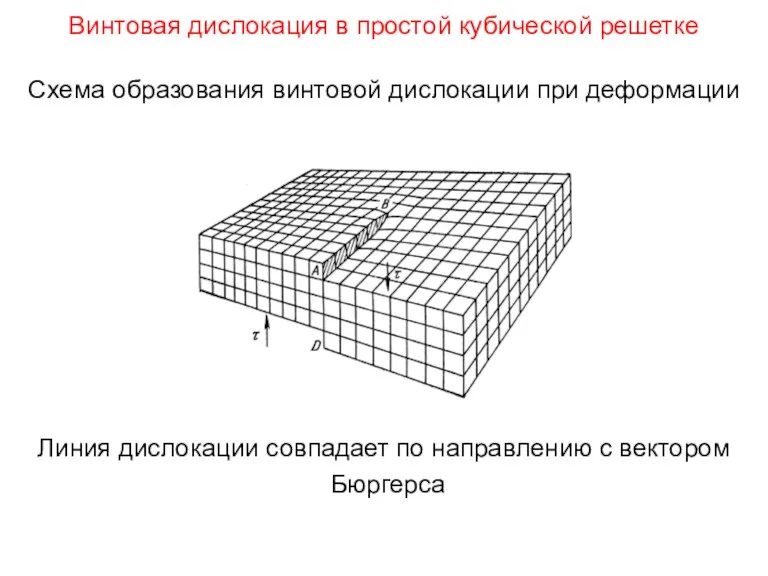
Винтовая дислокация в простой кубической решетке
Схема образования винтовой дислокации при деформации
Линия дислокации совпадает по направлению с вектором
Бюргерса

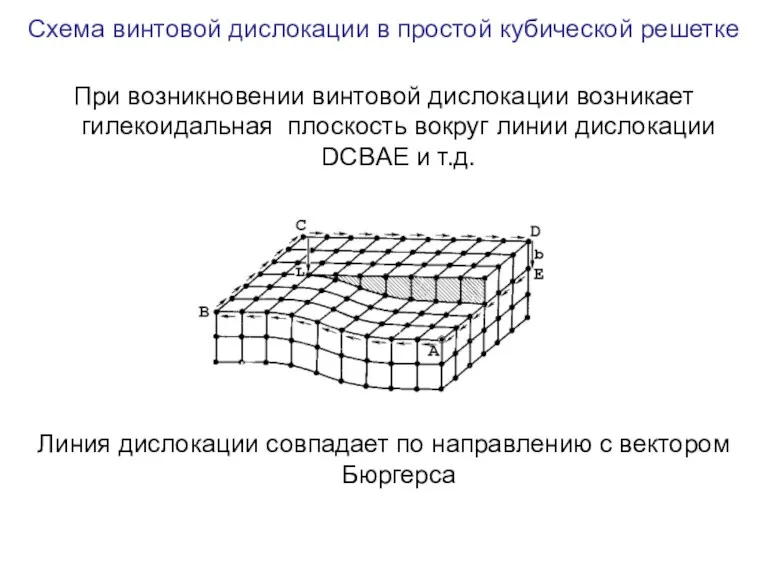
Схема винтовой дислокации в простой кубической решетке
При возникновении винтовой дислокации возникает гилекоидальная плоскость вокруг линии дислокации DCBAE и т.д.
Линия дислокации совпадает по направлению с вектором Бюргерса